
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
некоторые основополагающие результаты второго метода ляпунова
2.1 Основные теоремы Ляпунова
Сначала рассмотрим результаты, сформулированные и доказанные А.М. Ляпуновым и называемые в научной литературе основными теоремами Ляпунова.
Пусть дана приведенная по Ляпунову система (см. п. 1.3)
 (2.1.1)
(2.1.1)
с областью определения правых частей  вида
вида
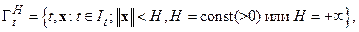 (2.1.2)
(2.1.2)
причем функция  удовлетворяет следующим свойствам в области (2.1.2):
удовлетворяет следующим свойствам в области (2.1.2):
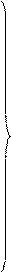 а) f- непрерывна по t и x;
а) f- непрерывна по t и x;
б) f- непрерывно дифференцируема по xи
(вследствие непрерывности по известной теореме
Вейерштрасса)все частные производные 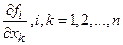 ,
,
ограничены на любом компактном подмножестве (2.1.3)
из области (2.1.2);
в) 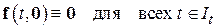 , т.е. система
, т.е. система
(2.1.1) допускает тривиальное решение 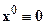 .
.
Первая теорема Ляпунова об устойчивости (А.М. Ляпунов, 1892).
Пусть найдется функция Ляпунова 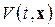 , непрерывно дифференцируемая по t, x в некоторой области
, непрерывно дифференцируемая по t, x в некоторой области 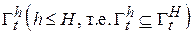 и такая, что в этой области
и такая, что в этой области 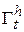 она:
она:
1) 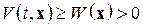 (2.1.4)
(2.1.4)
где 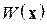 – некоторая не зависящая от времени положительно определенная функция Ляпунова;
– некоторая не зависящая от времени положительно определенная функция Ляпунова; 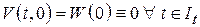 , т. е.
, т. е. 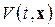 – положительно определенная функция Ляпунова в
– положительно определенная функция Ляпунова в 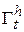 ;
;
2) ее полная производная, вычисленная в силу системы (2.1.1)
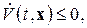 (2.1.5)
(2.1.5)
т.е. 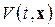 – знакопостоянная отрицательная функция Ляпунова в области
– знакопостоянная отрицательная функция Ляпунова в области 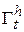 .
.
Тогда тривиальное решение 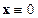 , приведенной системы (2.1.1)÷(2.1.3) устойчиво по Ляпунову при
, приведенной системы (2.1.1)÷(2.1.3) устойчиво по Ляпунову при 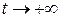 (в смысле данного в п. 1.2 определения устойчивости по Ляпунову при
(в смысле данного в п. 1.2 определения устойчивости по Ляпунову при 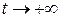 тривиального решения системы).■
тривиального решения системы).■
В качестве примера рассмотрим подробно доказательство этой теоремы, основанное, как и все доказательства результатов второго метода Ляпунова, на исследовании поведения функции (или функций) Ляпунова и ее полной производной, вычисленной в силу системы, т.е. на решениях системы, или, как говорят, вдоль решений системы. При этом целью доказательства является, опираясь на язык 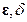 - окрестностей, показать, что из условий теоремы следует свойство тривиального решения, подпадающее под «юрисдикцию» соответствующего определения 1’ устойчивости по Ляпунову при
- окрестностей, показать, что из условий теоремы следует свойство тривиального решения, подпадающее под «юрисдикцию» соответствующего определения 1’ устойчивости по Ляпунову при 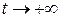 (п. 1.2).
(п. 1.2).
Доказательство [1]. На основании условия (2.1.4) теоремы рассмотрим в 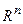 по любому
по любому 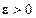 сферу
сферу 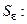
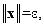
целиком лежащую в области 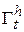 непрерывной дифференцируемости данной функции Ляпунова
непрерывной дифференцируемости данной функции Ляпунова 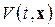 (2.1.4), т.е.
(2.1.4), т.е.
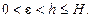
Так как сфера  - компактное множество и функция
- компактное множество и функция 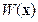 непрерывна и положительна на
непрерывна и положительна на  , то, в силу теоремы Вейерштрасса, точная нижняя грань этой функции достигается в некоторой точке
, то, в силу теоремы Вейерштрасса, точная нижняя грань этой функции достигается в некоторой точке
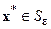
и, следовательно,
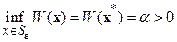 (2.1.6)
(2.1.6)
Пусть теперь 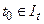 произвольно. Функция
произвольно. Функция 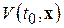 по условиям теоремы непрерывна по x и
по условиям теоремы непрерывна по x и 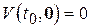 . Следовательно, существует окрестность
. Следовательно, существует окрестность
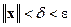
такая, что выполняется неравенство
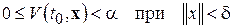 (2.1.7)
(2.1.7)
Рассмотрим любое нетривиальное решение системы (2.1.1)
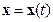 . (2.1.8)
. (2.1.8)
с начальным условием
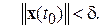
Докажем, что траектория этого решения целиком остается внутри сферы  , т.е.
, т.е.
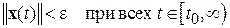 . (2.1.9)
. (2.1.9)
В силу выбора 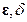 - окрестностей при
- окрестностей при 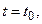 уже имеем
уже имеем
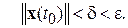
Докажем справедливость предположения (2.1.9) «от противного»: пусть неравенство (2.1.9) выполнено не для всех 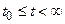 и
и 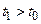 - точка первого выхода решения
- точка первого выхода решения 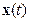 на границу сферы
на границу сферы  , т.е.
, т.е. 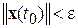 при
при 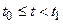 и
и 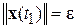 . Исследуем поведение функции Ляпунова (2.1.4) вдоль решения
. Исследуем поведение функции Ляпунова (2.1.4) вдоль решения 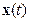 , обозначая:
, обозначая:

Так как в силу условия (2.15) теоремы
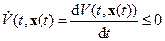 ,
,
то функция 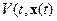 невозрастающая. Следовательно, учитывая формулы (2.1.7) и (2.1.6), имеем:
невозрастающая. Следовательно, учитывая формулы (2.1.7) и (2.1.6), имеем:
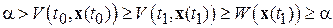 ,
,
т.е. получили противоречие, что и доказывает справедливость неравенства (2.1.9) для всех 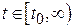 .
.
Мы исчерпали все условия теоремы, следовательно, можно подводить итоги доказательства, а именно, произвольно взятое решение 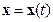 при любом конечном
при любом конечном 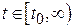 остается внутри сферы
остается внутри сферы  , а значит так как
, а значит так как 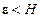 , это решение бесконечно продолжимо вправо, т.е. определено при всех
, это решение бесконечно продолжимо вправо, т.е. определено при всех 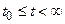 , причем оно навсегда остается внутри
, причем оно навсегда остается внутри  -окрестности, т.е.
-окрестности, т.е.
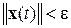 при всех
при всех 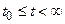 ,
,
если только оно начинается внутри 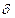 -окрестности, т.е.
-окрестности, т.е.
 .
.
Таким образом, согласно определению 1’ устойчивости по Ляпунову (см. п. 1.2) тривиальное решение 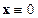 системы (2.1.1) устойчиво по Ляпунову при
системы (2.1.1) устойчиво по Ляпунову при 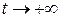 , что и требовалось доказать. □
, что и требовалось доказать. □
Следствие. Если выполняются условия теоремы для системы (2.1.1)÷(2.1.3), то все ее решения 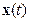 , начинающиеся внутри некоторой «достаточно малой»
, начинающиеся внутри некоторой «достаточно малой»  -окрестности
-окрестности
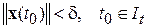
бесконечно продолжимы вправо и ограничены на всем полубесконечном интервале 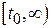 .■
.■
Мы рассмотрели один из многих вариантов подробного доказательства первой теоремы Ляпунова, близкого по форме к классическим рассуждениям, характерным для самого основателя метода функций Ляпунова, доказавшего ее в 1892 г. В качестве другого примера доказательства этой теоремы приведем более компактное доказательство и для этого прибегнем к рассмотренным выше (см. п. 1.5) функциям Хана вида 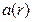 .
.
Запишем формулировку в терминах функций Хана [5].
Первая теорема Ляпунова об устойчивости (А.М. Ляпунов (1892 г.) (в терминах функций Хана).
Если для системы (2.1.1)÷(2.1.3) существует функция Ляпунова 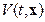 , непрерывно дифференцируемая по t и x в области
, непрерывно дифференцируемая по t и x в области 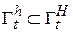 и такая, что для некоторой функции Хана
и такая, что для некоторой функции Хана 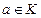 и t , xиз области
и t , xиз области 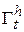 :
:
1) 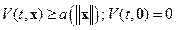 ;
;
2) 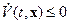 ,
,
то тривиальное решение системы (2.1.1) устойчиво (по Ляпунову при 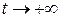 ).■
).■
Доказательство. Пусть заданы 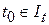 и
и 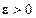 . Так как V непрерывна и
. Так как V непрерывна и 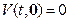 , то найдется
, то найдется 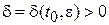 , такое, что
, такое, что
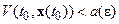 для всех
для всех 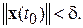
Рассмотрим все решения с начальными данными 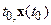 :
:
 ,
,
начинающиеся из 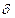 -окрестности . Используя условие (2) теоремы, для любых
-окрестности . Используя условие (2) теоремы, для любых 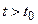 и
и  получаем
получаем
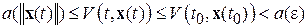 .
.
Поскольку 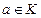 , то заключаем, что
, то заключаем, что 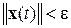 .□ Теорема доказана.
.□ Теорема доказана.
Замечания.
1. Сравнение приведенных двух вариантов формулировок и доказательств первой теоремы Ляпунова позволяет оценить компактность и лаконичность современного языка математической теории систем.
2. В дальнейшем изложении ограничимся кратким обзором некоторых результатов второго метода Ляпунова , как правило, комментируя их, но не сопровождая подробными доказательствами, которые можно найти в литературных источниках, список которых приведен в конце изложения всего материала. ■
Вторая теорема Ляпунова об асимптотичности устойчивости (А.М. Ляпунов, 1892 г. )
Пусть дана приведенная система (2.1.1) ÷ (2.1.3) и пусть в некоторой области 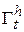 найдется функция Ляпунова
найдется функция Ляпунова 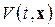 , непрерывно дифференцируемая в этой области, и такая, что найдутся три не зависящие от времени положительно определенные функции Ляпунова
, непрерывно дифференцируемая в этой области, и такая, что найдутся три не зависящие от времени положительно определенные функции Ляпунова
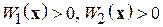 и
и 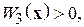
такие, что выполняются следующие соотношения (в области 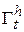 ):
):
1) 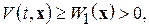 т. е.
т. е. 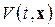 – положительно определенная;
– положительно определенная;
2) 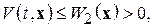 т. е.
т. е. 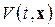 допускает сильный БМВП при
допускает сильный БМВП при 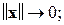
3) полная производная по времени в силу системы (2.1.1) 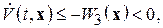 т. е.
т. е.  – отрицательно определенная в
– отрицательно определенная в 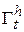 .
.
Тогда тривиальное решение приведенной системы (2.1.1) асимптотически устойчиво при 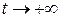 с областью аттрактивности (с областью притяжения)
с областью аттрактивности (с областью притяжения) 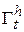 . ■
. ■
Замечание. Не будем рассматривать, как условились, полное доказательство этой теоремы, а ограничимся некоторыми комментариями, опирающимися на геометрический смысл полной производной (см. п. 1.7).
Сначала заметим, что из первого и третьего условий теоремы следует устойчивость по Ляпунову тривиального решения в силу первой теоремы Ляпунова. Но, в силу наличия третьего условия – отрицательной определенности полной производной, произвольное решение 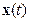 не может «застаиваться» ни в какой
не может «застаиваться» ни в какой  -окрестности, в которой сохраняется отрицательность производной, а наличие БМВП при
-окрестности, в которой сохраняется отрицательность производной, а наличие БМВП при 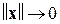 (второе условие) позволяет этой
(второе условие) позволяет этой  -окрестности быть сколь угодно малой. Поэтому отрицательность производной будет «заставлять» решение
-окрестности быть сколь угодно малой. Поэтому отрицательность производной будет «заставлять» решение 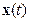 переходить во все «меньшие» и «меньшие»
переходить во все «меньшие» и «меньшие»  -окрестности, пока решение
-окрестности, пока решение 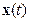 не «сольется» с началом координат
не «сольется» с началом координат 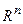 при
при 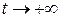 , что и означает асимптотическую устойчивость тривиального решения системы.
, что и означает асимптотическую устойчивость тривиального решения системы.
Причем такое поведение характерно для каждого решения, начинающегося в области 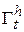 , в которой выполняются все три условия теоремы, а, следовательно, эта область и является областью притяжения тривиального решения системы (2.1.1).■
, в которой выполняются все три условия теоремы, а, следовательно, эта область и является областью притяжения тривиального решения системы (2.1.1).■
Определение 6 (неустойчивости по Ляпунову). Тривиальное решение (положение равновесия) 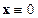 называется неустойчивым по Ляпунову, если для некоторых
называется неустойчивым по Ляпунову, если для некоторых 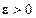 ,
, 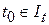 и любого
и любого 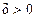 существует (хотя бы одно) решение
существует (хотя бы одно) решение 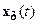 и момент времени
и момент времени 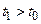 такие, что
такие, что
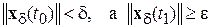 .■
.■
Третья теорема Ляпунова о нейстойчивости (А.М. Ляпунова, 1892 г.)
Пусть дана приведенная система (2.1.1)÷(2.1.3) и пусть для нее найдется непрерывно дифференцируемая по t и x в некоторой области 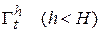 функция Ляпунова
функция Ляпунова 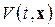 , допускающая БМВП при
, допускающая БМВП при 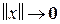 и обладающая знакоопределенной производной
и обладающая знакоопределенной производной  , вычисленной в силу системы.
, вычисленной в силу системы.
Если при некотором 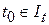 в любой окрестности
в любой окрестности 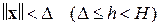 найдется точка
найдется точка 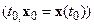 , для которой знак функции V одинаков со знаком производной
, для которой знак функции V одинаков со знаком производной 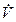 , т.е. такая, что
, т.е. такая, что
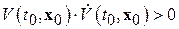 , (2.1.10)
, (2.1.10)
то тривиальное решение системы (2.1.1) неустойчиво по Ляпунову. ■
Без доказательства.
2.2 Другие теоремы метода функций Ляпунова
Теоретические основы метода функций Ляпунова, заложенные А.М. Ляпуновым в его основополагающем труде (1892 г.), стали универсальным инструментом исследования свойств устойчивости нелинейных систем. Уже в основных теоремах можно заметить, как варьируя, видоизменяя и комбинируя свойства функций Ляпунова и ее полной производной, вычисленной в силу системы, можно открывать, формулировать и доказывать те или иные свойства поведения решений системы. В этом состоит универсальность и провиденциальность (от лат. Providentio - предвижу) метода функций Ляпунова.
Рассмотрим некоторые результаты, расширяющие и усиливающие в различных направлениях свойства устойчивости тривиального решения нелинейной системы (1.2.1)÷(1.2.3).
Одно из таких направлений связано с равномерной устойчивостью, введенной определением 3 (п. 1.2).
Теорема о равномерной устойчивости (К.П. Персидский, 1933).
Пусть дана приведенная система (2.1.1) ÷ (2.1.3). Если в некоторой области 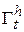 существует функция Ляпунова
существует функция Ляпунова 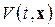 , непрерывно дифференцируемая по t, x в этой области, и найдутся две независимых от времени положительно определенных функций Ляпунова вида
, непрерывно дифференцируемая по t, x в этой области, и найдутся две независимых от времени положительно определенных функций Ляпунова вида 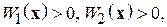 таких что:
таких что:
1) 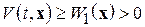 (положительная определенность
(положительная определенность 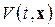 )
)
2) 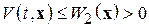 (сильный БМВП при
(сильный БМВП при 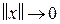 )
)
3) 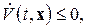 (знакопостоянная отрицательная),
(знакопостоянная отрицательная),
то тривиальное решение системы (2.1.1) устойчиво по Ляпунову при 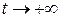 равномерно по
равномерно по 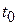 (равномерно на
(равномерно на 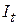 )
)
(Без доказательства).
Замечание.Нетрудно видеть, что условия теоремы К.П. Персидского являются комбинацией требований к функции V и ее производной 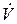 , содержащихся в первой и второй теоремах Ляпунова, а именно, функция V здесь удовлетворяет второй теореме, а ее производная
, содержащихся в первой и второй теоремах Ляпунова, а именно, функция V здесь удовлетворяет второй теореме, а ее производная 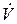 - первой теореме.
- первой теореме.
В свете сказанного легко увидеть, что основные теоремы об устойчивости и асимптотической устойчивости содержат требования, удовлетворение которых придает поведению решений исследуемой системы свойства, не планируемые в определениях 1 и 2 (п. 1.2). В этом сказывается провиденческая сила второго метода.
Определение 7 (равномерной асимптотической устойчивости). Тривиальное решение системы (2.1.1.)÷(2.1.3) называется асимптотически устойчивым равномерно по времени 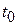 и начальным возмущениям
и начальным возмущениям 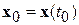 , или просто равномерно асимптотически устойчивым, если оно асимптотически устойчиво при
, или просто равномерно асимптотически устойчивым, если оно асимптотически устойчиво при 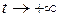 (в смысле определения 2 (п. 1.2)) и, кроме того, для любого числа
(в смысле определения 2 (п. 1.2)) и, кроме того, для любого числа 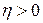 можно указать положительное число
можно указать положительное число 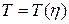 (зависящее от выбора
(зависящее от выбора 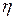 ), такое, что
), такое, что
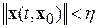 , если
, если 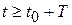 ,
,
каковы бы ни были начальный момент времени 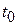 и начальные возмущения
и начальные возмущения 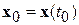 из области притяжения
из области притяжения 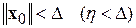 .■
.■
Теорема о равномерной асимптотической устойчивости (Н.Н. Красовский, 1959)
Тривиальное решение системы (2.1.1.)÷(2.1.3) равномерно асимптотически устойчиво (в смысле определения 7), если выполняются все условия второй теоремы Ляпунова (асимптотической устойчивости). ■
Замечание. Таким образом, решения нелинейной системы, удовлетворяющей требования второй теоремы Ляпунова, облают свойствами, не запланированными в определении 2 (п. 2.1). Этот результат был замечен и доказан академиком Н.Н. Красовским (1959) [2]. Более того, можно указать оценку [2,3,4] времени Т
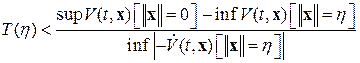 (2.2.1)
(2.2.1)
приближения решения к тривиальному решению (говорят, к началу координат в 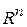 , или просто к началу) при его переходе из
, или просто к началу) при его переходе из 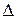 -окрестности в
-окрестности в 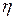 -окрестность.■
-окрестность.■
Можно указать еще одно из направлений модификации теорем второго метода Ляпунова, связанного с важным свойством глобальной сходимости решений нелинейной системы, задаваемым определением 3 (п. 1.2).
Привлекая свойства ББНП при 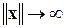 (см. п. 1.4, определение 7), Е.А. Барбашин и Н.Н. Красовский доказали следующую теорему [2].
(см. п. 1.4, определение 7), Е.А. Барбашин и Н.Н. Красовский доказали следующую теорему [2].
Теорема Барбашина – Красовского (о глобальной асимптотической устойчивости).
Пусть приведенная система (2.1.1) определена на полупространстве
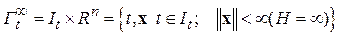 (2.2.2)
(2.2.2)
или, как говорят, на всем 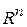 , и пусть для нее в области определения (2.2.2) найдутся функция Ляпунова
, и пусть для нее в области определения (2.2.2) найдутся функция Ляпунова 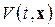 и три не зависящие от времени функции Ляпунова.
и три не зависящие от времени функции Ляпунова.
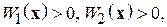 и
и 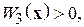
положительно определенные и такие, что:
1) 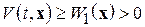 (положительная определенность функции
(положительная определенность функции 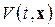 );
);
2) 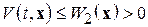 (сильный БМВП при
(сильный БМВП при 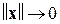 функции
функции 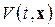 );
);
3) 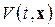 допускает ББНП при
допускает ББНП при  (заметим, что условия (2) и (3) могут быть объединены в свойство существования бесконечного предела для
(заметим, что условия (2) и (3) могут быть объединены в свойство существования бесконечного предела для 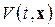 ;
;
4)  (отрицательная определенность
(отрицательная определенность  , вычисленной в силу системы (2.1.1)).
, вычисленной в силу системы (2.1.1)).
Тогда тривиальное решение системы асимптотически устойчиво в целом, или глобально асимптотически устойчивости.■
Без доказательства (см. [2]).
| <== предыдущая страница | | | следующая страница ==> |
| Тема № 11.Социальные проекты и структура проектной деятельности | | |
Дата добавления: 2014-10-17; просмотров: 479; Нарушение авторских прав

Мы поможем в написании ваших работ!