
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Распределение Больцмана
При рассмотрении распределения Максвелла предполагалось, что молекулы равномерно распределены по объему сосуда. Это справедливо, если сосуд небольшой. В больших по объему сосудах равномерность распределения молекул нарушается из-за действия силы тяжести, в связи с этим плотность и число молекул в единице объема будут неодинаковыми.
Рассмотрим, как изменяется давление атмосферы Земли в зависимости от высоты. Пусть на поверхности Земли (h=0) давление атмосферы 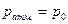 . На высоте h давление р. При увеличении высоты на
. На высоте h давление р. При увеличении высоты на 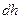 давление уменьшается на
давление уменьшается на 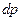 , где
, где 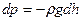 (
( 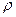 - плотность воздуха на данной высоте). Используя уравнение состояния идеального газа
- плотность воздуха на данной высоте). Используя уравнение состояния идеального газа 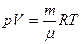 , с учетом
, с учетом 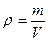
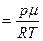 , получим
, получим 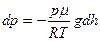 . Разделим переменные
. Разделим переменные 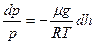 и проинтегрируем от
и проинтегрируем от 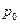 до
до 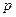 , от 0 до h:
, от 0 до h: 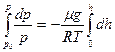 ,
, 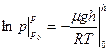 или
или 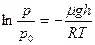 , или
, или 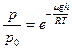 , или
, или 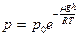 (1). Это выражение называют барометрической формулой Больцмана.
(1). Это выражение называют барометрической формулой Больцмана.
С учетом того, что 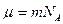 ,
, 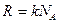 (
( 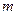 - масса одной молекулы), можно записать
- масса одной молекулы), можно записать 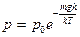 .
.
Барометрическая формула показывает зависимость давления газа от высоты над поверхностью Земли. Если учесть, что концентрация молекул воздуха в атмосфере определяет давление ( 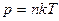 ), то, воспользовавшись уравнением (1), получим
), то, воспользовавшись уравнением (1), получим 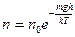 (2).
(2).
Из (2) следует, что с понижением температуры число частиц на высоте 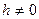 убывает и при
убывает и при 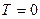 К обращается в нуль, т.е. при абсолютном нуле все молекулы расположились бы на земной поверхности. При высоких температурах, напротив, концентрация молекул
К обращается в нуль, т.е. при абсолютном нуле все молекулы расположились бы на земной поверхности. При высоких температурах, напротив, концентрация молекул 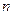 слабо убывает с высотой, так что молекулы оказываются распределенными по высоте почти равномерно.
слабо убывает с высотой, так что молекулы оказываются распределенными по высоте почти равномерно.
Этот факт имеет следующее физическое объяснение. Распределение молекул по высоте 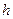 устанавливается в результате действия двух факторов:
устанавливается в результате действия двух факторов:
1) притяжение молекул к Земле (сила тяжести) стремится расположить их на поверхности Земли;
2) тепловое движение (характеризуемое величиной 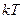 ) стремится разбросать молекулы равномерно по всей высоте.
) стремится разбросать молекулы равномерно по всей высоте.
Чем больше масса и меньше температура, тем сильнее преобладает первая тенденция, молекулы сгущаются у поверхности Земли. В пределе при 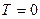 К тепловое движение совсем прекращается и под влиянием притяжения молекулы располагаются у Земной поверхности. При высоких температурах превалирует тепловое движение и плотность молекул медленно убывает с высотой.
К тепловое движение совсем прекращается и под влиянием притяжения молекулы располагаются у Земной поверхности. При высоких температурах превалирует тепловое движение и плотность молекул медленно убывает с высотой.
На различной высоте молекула обладает различным запасом потенциальной энергии: 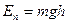 . Отсюда, распределение молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. Можно записать
. Отсюда, распределение молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. Можно записать
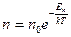 (3) -
(3) -
Это выражение называют распределением Больцмана (или законом Больцмана), где 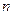 - концентрация молекул в том месте пространства, где потенциальная энергия имеет значение
- концентрация молекул в том месте пространства, где потенциальная энергия имеет значение 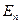 ,
, 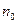 - концентрация молекул в том месте, где
- концентрация молекул в том месте, где 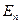 =0.
=0.
Из (3) видно, что молекулы располагаются с большей плотностью там, где меньше их 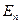 , и, наоборот, с меньшей плотностью в местах, где их
, и, наоборот, с меньшей плотностью в местах, где их 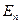 больше.
больше.
Больцман показал, что это распределение справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любого числа одинаковых частиц, находящихся в состоянии хаотического теплового движения.
В то же время, как закон Максвелла дает распределение частиц по 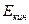 , закон Больцмана дает распределение по значениям
, закон Больцмана дает распределение по значениям 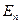 . Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение
. Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение 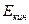 или
или 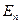 одной молекулы к величине, определяющей среднюю энергию теплового движения молекулы (
одной молекулы к величине, определяющей среднюю энергию теплового движения молекулы ( 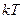 ).
).
| <== предыдущая страница | | | следующая страница ==> |
| Распределение Максвелла | | | Явления переноса |
Дата добавления: 2014-11-08; просмотров: 348; Нарушение авторских прав

Мы поможем в написании ваших работ!