Распределение Максвелла

При рассмотрении давления и выводе формулы для давления на основании представлений о газе, как о совокупности движущихся хаотическим образом частиц мы ввели понятие средней скорости и предположили, что все частицы имеют одинаковую скорость. Это предположение верно для упрощенной модели, пригодной для вывода уравнения состояния. Реально из-за соударения молекул (атомов) друг с другом и со стенками сосуда, всегда имеются молекулы (атомы) с относительно малыми скоростями и молекулы (атомы) с повышенными скоростями.

Один из важнейших вопросов физики заключается в том, каким будет распределение частиц по скоростям (то есть какое число частиц будет иметь скорость в интервале от 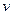до 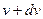). Этот вопрос был изучен английским физиком Максвеллом, и найденная им зависимость получила название распределения Максвелла.

Пусть dN – число частиц, скорости которых лежат в интервале от 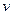до 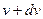. Очевидно, что dN будет увеличиваться с ростом интервала 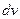. Т.е. 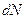~ 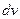. В то же время dN будет увеличиваться, чем больше общее число частиц N. Т.о. 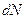~ 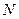. Отсюда 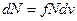, где 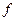- коэффициент пропорциональности. Число 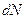будет зависеть от того, где будем брать интервал скоростей, поэтому 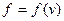. Получаем .

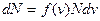Разделим обе части равенства на 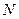: 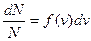, но 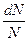- это вероятность того, что модуль скорости молекулы окажется в пределах от 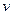до 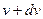. Отсюда 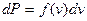или 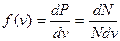- это плотность вероятности (т.е. вероятность, приходящаяся на единичный интервал скоростей, или вероятность того, что частица будет иметь заданную скорость в единичном интервале скоростей).

Максвелл нашел вид функции 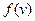. Строгое доказательство громоздко, запишем готовый результат: 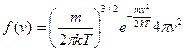(1).

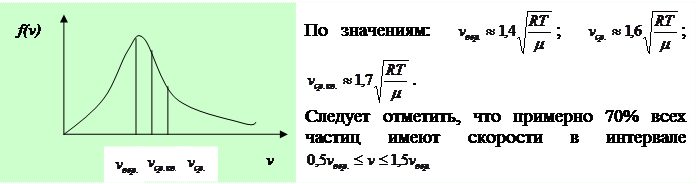
Эту функцию называют функцией распределения молекул газа по скоростям.Графически эта функция выглядит следующим образом: 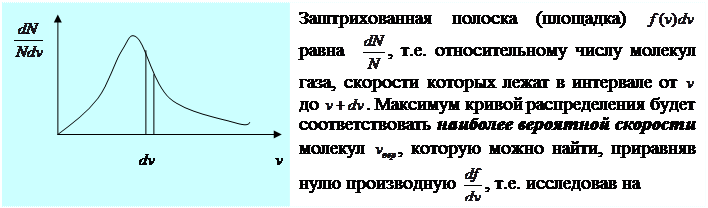исследовав на экстремум функцию (1). Опустив в выражении (1) постоянные множител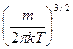и и 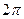, получим для нахождения : .

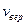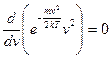После дифференцирования имеем: 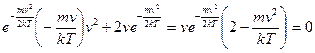. Удовлетворяющие этому уравнению значения 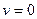и 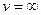соответствуют минимуму функции (смотреть график). Отсюда, значение 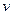, отвечающее максимуму, будет: 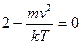, т.е. 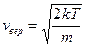или .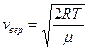

Средняя скорость молекул определяется как 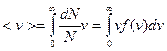, где 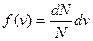. Интеграл берут по частям и получают 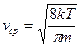или 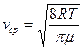. Эту скорость называют средней арифметической скоростью.

Средняя квадратичная скорость определяется как 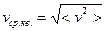(из 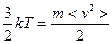; 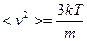). Отсюда .

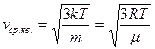Из полученных формул видно, что 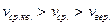На графике:

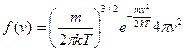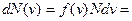
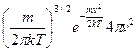
Используя распределение молекул идеального газа по скоростям, т.е. , имеем 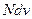. Найдем распределение по энергиям.

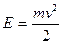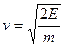Так как молекулы газа обладают кинетической энергией , то и 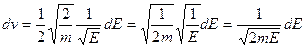. Перейдя от переменной 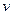к 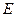, получим

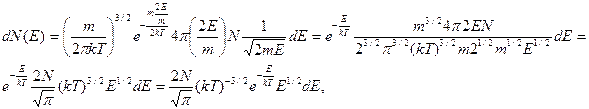
где 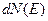- число молекул, имеющих кинетическую энергию от 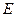до .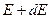

Функция распределения молекул по энергиям имеет вид:

.

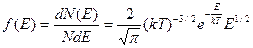Средняя кинетическая энергия молекулы идеального газа определяется интегралом: .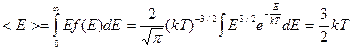

Впервые закон Максвелла о распределении молекул по скоростям и энергиям был экспериментально подтвержден в опытах Штерна. Опыт состоял в следующем: брали платиновую нить, покрытую серебром, ее помещали в цилиндр (при этом нить располагали по оси цилиндра, в цилиндре есть узкая щель), все заключали в другой цилиндр. При нагревании проволоки током серебро испаряется, атомы вылетают через щель и попадают на внутреннюю поверхность цилиндра. Если оба цилиндра неподвижны, то все атомы серебра попадают в одну и ту же точку, независимо от их скорости. При одновременном вращении обоих цилиндров с угловой скоростью ω атомы серебра (в зависимости от скорости) попадают в другую точку на стенке цилиндра, так как за время полета от точки О до стенки цилиндр успевает повернуться.

Дата добавления: 2014-11-08; просмотров: 558; Нарушение авторских прав

Мы поможем в написании ваших работ!