
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Статистические распределения
Прежде чем говорить о распределениях, введем понятия вероятности и флуктуации.
Пусть имеется очень большое число N одинаковых молекул, находящихся в равновесии. Если бы удалось измерить некоторую величину х, характеризующую молекулу (например, энергию, скорость и т.д.), у N молекул, то оказалось бы, что у N1 молекул величина х имеет значение х1, у N2 – значение х2, у Ni - значение хi. Величину  называют относительной частотой появления результата хi. Предел этой величины, когда N
называют относительной частотой появления результата хi. Предел этой величины, когда N 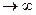 , т.е.
, т.е. 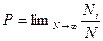 , называют вероятностью появления результата хi. Так как
, называют вероятностью появления результата хi. Так как 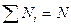 , то
, то 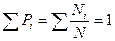 , т.е. сумма вероятностей всех возможных значений величины х равна 1.
, т.е. сумма вероятностей всех возможных значений величины х равна 1.
Вероятность получить результат хi или хk равна: 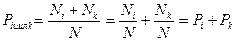 - это выражение называют теоремой сложения вероятностей.
- это выражение называют теоремой сложения вероятностей.
Допустим, что молекулы характеризуют значениями двух величин х и у. Вероятности этих значений равны: 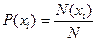 и
и 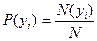 (х и у могут принимать дискретные значения). Вероятность того, что молекулы имеют одновременно значения хi и уi равна:
(х и у могут принимать дискретные значения). Вероятность того, что молекулы имеют одновременно значения хi и уi равна: 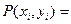
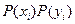 - теорема об умножении вероятностей.
- теорема об умножении вероятностей.
Если мы знаем вероятности появления различных результатов измерения, то можем найти среднее значение всех результатов: 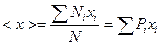 .
.
Если величина х, характеризующая систему может принимать непрерывный ряд значений (в частности 0<x<∞), например модуль поступательной скорости и кинетической энергии молекул, то число возможных значений х бесконечно велико.
В этом случае удобно рассмотреть вероятность 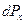 того, что величина имеет значения, заключенные в пределах малого интервала от х до х+dx:
того, что величина имеет значения, заключенные в пределах малого интервала от х до х+dx: 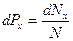 . При малом интервале dx эта вероятность будет пропорциональна dx. Кроме того, она зависит от того, в каком месте оси х расположен интервал dx , т.е. является функцией x (f(x)) . Таким образом,
. При малом интервале dx эта вероятность будет пропорциональна dx. Кроме того, она зависит от того, в каком месте оси х расположен интервал dx , т.е. является функцией x (f(x)) . Таким образом, 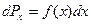 ,
, 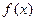 - эту функцию называют функцией распределения вероятностей.
- эту функцию называют функцией распределения вероятностей.
Умножив 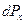 на полное число молекул N, обладающих значениями от х до х+dx:
на полное число молекул N, обладающих значениями от х до х+dx: 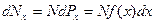 . Интеграл от
. Интеграл от 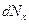 , взятый по всему интервалу возможных значений х, должен быть равен числу молекул N:
, взятый по всему интервалу возможных значений х, должен быть равен числу молекул N: 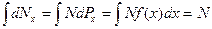 . Отсюда следует
. Отсюда следует 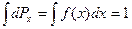 .
.
|

| <== предыдущая страница | | | следующая страница ==> |
| Закон равнораспределения энергии по степеням свободы молекулы | | | Распределение Максвелла |
Дата добавления: 2014-11-08; просмотров: 255; Нарушение авторских прав

Мы поможем в написании ваших работ!