
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПРЯМЫЕ И ПЛОСКОСТИ
§ 2.1. АФФИННЫЕ РЕПЕРЫ И КООРДИНАТЫ ТОЧЕК.
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ КООРДИНАТ ТОЧЕК
Аффинные реперы являются обобщением известных из средней школы систем координат на плоскости и в пространстве. Чтобы задать аффинный реперна прямой, на плоскости или в пространстве, надо зафиксировать точку и выбрать базис соответствующего множества векторов.
Определение 2.1.1. Аффинным репером на прямой 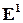 называется набор
называется набор 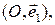 где
где  – точка,
– точка, 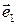 – базис множества
– базис множества 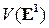 векторов прямой, т.е. ненулевой вектор прямой (рис. 1). Координатой точки
векторов прямой, т.е. ненулевой вектор прямой (рис. 1). Координатой точки 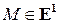 в репере
в репере 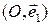 называется координата радиус-вектора
называется координата радиус-вектора 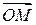 в базисе
в базисе 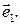
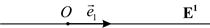
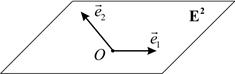
Рис. 1 Рис. 2
Таким образом, координата точки 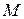 в репере
в репере 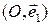 – это число
– это число 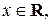 которое определяется равенством
которое определяется равенством 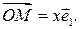 Координата для каждой точки определяется однозначно, так как отображение
Координата для каждой точки определяется однозначно, так как отображение 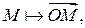 ставящее в соответствие точке ее радиус-вектор, есть биекция множества точек прямой
ставящее в соответствие точке ее радиус-вектор, есть биекция множества точек прямой 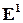 на множество векторов
на множество векторов 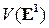 этой прямой, а координата вектора в данном базисе определяются однозначно (теорема ). Если считать, что масштаб на прямой определяется вектором
этой прямой, а координата вектора в данном базисе определяются однозначно (теорема ). Если считать, что масштаб на прямой определяется вектором 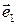 (т.е.
(т.е.  ), то координата точки на прямой имеет тот же смысл, что и в средней школе. Прямую с фиксированным репером
), то координата точки на прямой имеет тот же смысл, что и в средней школе. Прямую с фиксированным репером 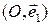 будем называть координатной осью и обозначать
будем называть координатной осью и обозначать 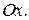 Если
Если 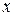 – координата точки
– координата точки 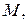 то используют запись
то используют запись 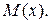
Определение 2.1.2. Аффинным репером на плоскости 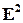 называется набор
называется набор 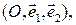 где
где  – точка плоскости,
– точка плоскости, 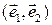 – базис множества
– базис множества 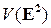 векторов плоскости, т.е. упорядоченная пара неколлинеарных векторов плоскости (рис. 2). Координатами точки
векторов плоскости, т.е. упорядоченная пара неколлинеарных векторов плоскости (рис. 2). Координатами точки 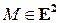 в репере
в репере 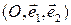 называется координаты радиус-вектора
называется координаты радиус-вектора 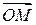 точки
точки 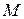 в базисе
в базисе 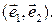
Таким образом, координаты точки 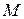 в репере
в репере 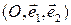 – это пара чисел
– это пара чисел 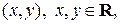 таких, что
таких, что 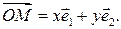 Если
Если 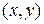 – координаты точки
– координаты точки 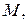 то используют запись
то используют запись 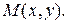 Те же аргументы, что и в случае прямой, показывают, что координаты точки в данном репере определяются однозначно. Имея репер
Те же аргументы, что и в случае прямой, показывают, что координаты точки в данном репере определяются однозначно. Имея репер 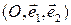 на плоскости, можно говорить о двух координатных осях. Координатная ось с репером
на плоскости, можно говорить о двух координатных осях. Координатная ось с репером 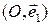 называется осью абсцисс и обозначается
называется осью абсцисс и обозначается 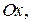 координатная ось с репером
координатная ось с репером 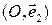 называется осью ординат и обозначается
называется осью ординат и обозначается 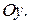 Первая
Первая 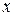 и вторая
и вторая 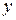 координаты точки называются соответственно абсциссой и ординатой этой точки. Способ определения координат векторов, изложенный в § 1.4, позволяет выяснить геометрический смысл координат. Для нахождения абсциссы
координаты точки называются соответственно абсциссой и ординатой этой точки. Способ определения координат векторов, изложенный в § 1.4, позволяет выяснить геометрический смысл координат. Для нахождения абсциссы 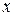 точки
точки 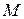 нужно спроектировать ее на ось
нужно спроектировать ее на ось 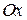 параллельно оси
параллельно оси 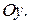 Если
Если 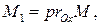 то
то 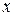 – координата точки
– координата точки 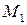 на оси абсцисс. Аналогично,
на оси абсцисс. Аналогично, 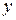 – координата точки
– координата точки 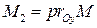 на оси ординат (рис. 3).
на оси ординат (рис. 3).
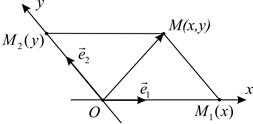
Рис. 3
Определение 2.1.3. Аффинным репером в пространстве 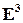 называется набор
называется набор 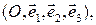 где
где  – точка,
– точка, 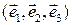 – базис множества
– базис множества 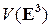 векторов пространства, т.е. упорядоченная тройка некомпланарных векторов.(рис. 4). Координатами точки
векторов пространства, т.е. упорядоченная тройка некомпланарных векторов.(рис. 4). Координатами точки 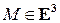 в репере
в репере  называется координаты радиус-вектора
называется координаты радиус-вектора 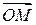 точки
точки 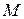 в базисе
в базисе 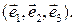
Таким образом, координаты точки 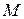 в репере
в репере  – это тройка чисел
– это тройка чисел 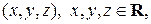 таких, что
таких, что 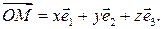 Если
Если 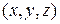 – координаты точки
– координаты точки 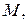 то используют запись
то используют запись 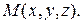 Далее можно повторить все то, что говорилось выше в случае плоскости с очевидными дополнениями. Помимо координатных осей абсцисс
Далее можно повторить все то, что говорилось выше в случае плоскости с очевидными дополнениями. Помимо координатных осей абсцисс 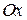 и ординат
и ординат 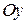 в пространстве добавляется осьаппликат
в пространстве добавляется осьаппликат 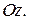 Кроме того, в пространстве имеются три координатные плоскости, определяемые парами осей: это плоскости
Кроме того, в пространстве имеются три координатные плоскости, определяемые парами осей: это плоскости 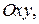
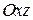 и
и 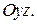 Каждая из координат
Каждая из координат 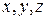 точки
точки 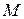 есть координата проекции точки
есть координата проекции точки 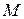 на соответствующую ось параллельно дополнительной координатной плоскости (рис. 4). Координаты точки в данном репере определяются однозначно.
на соответствующую ось параллельно дополнительной координатной плоскости (рис. 4). Координаты точки в данном репере определяются однозначно.
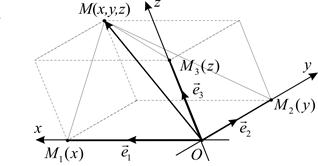
Рис. 4
Аффинные реперы называются также аффинными (или декартовыми) системами координат и обозначают: 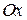 (для прямой),
(для прямой), 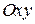 (для плоскости),
(для плоскости), 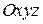 (для пространства). Точка
(для пространства). Точка 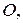 входящая в репер, называется началом системы координат. В случаях, когда
входящая в репер, называется началом системы координат. В случаях, когда 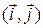 или
или 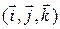 – ортонормированные базисы (определение 1.4.5), говорят об ортонормированном репере плоскости
– ортонормированные базисы (определение 1.4.5), говорят об ортонормированном репере плоскости 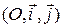 (рис. 5) и ортонормированном репере пространства
(рис. 5) и ортонормированном репере пространства 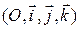 (рис. 6). Ортонормированные реперы называются также декартовыми прямоугольными системами координат.
(рис. 6). Ортонормированные реперы называются также декартовыми прямоугольными системами координат.
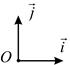
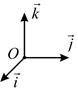
Рис. 5 Рис. 6
Замечание 2.1.1. Отметим две биекции, возникающие при координатизации прямой, плоскости или пространства. Пусть, например, 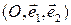 – аффинный репер на плоскости
– аффинный репер на плоскости 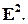 Тогда отображение
Тогда отображение 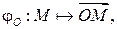 ставящее в соответствие каждой точке плоскости ее радиус-вектор, является биекцией множества точек плоскости
ставящее в соответствие каждой точке плоскости ее радиус-вектор, является биекцией множества точек плоскости 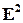 на множество
на множество 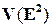 векторов плоскости. А отображение
векторов плоскости. А отображение 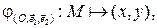 ставящее в соответствие каждой точке плоскости ее координаты, является биекцией множества точек плоскости
ставящее в соответствие каждой точке плоскости ее координаты, является биекцией множества точек плоскости 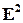 на множество
на множество 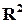 пар вещественных чисел. Аналогично в случаях прямой и пространства биекциями являются отображения
пар вещественных чисел. Аналогично в случаях прямой и пространства биекциями являются отображения
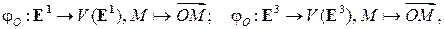
а также отображения
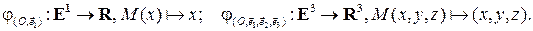
Утверждение 2.1.1. (i) Пусть 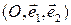 – аффинный репер на плоскости
– аффинный репер на плоскости 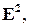
 – произвольные точки плоскости, заданные своими координатами в данном репере. Тогда:
– произвольные точки плоскости, заданные своими координатами в данном репере. Тогда:
(i) вектор 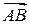 в базисе
в базисе 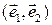 имеет следующие координаты:
имеет следующие координаты: 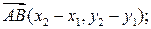
(ii) середина 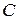 отрезка
отрезка 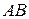 имеет координаты:
имеет координаты: 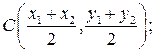
(iii) если 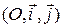 – ортонормированный репер, то расстояние между точками
– ортонормированный репер, то расстояние между точками 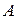 и
и 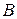 вычисляется по формуле:
вычисляется по формуле:
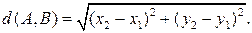 (1)
(1)
Доказательство. (i) По определению 2.1.2, координаты точек 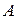 и
и 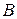 совпадают с координатами векторов
совпадают с координатами векторов 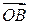 и
и 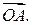 Так как
Так как 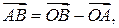 то, согласно утверждению 1.4.5, каждая координата вектора есть разность соответствующих координат векторов
то, согласно утверждению 1.4.5, каждая координата вектора есть разность соответствующих координат векторов 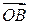 и
и 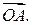
(ii) Пусть 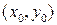 – координаты точки
– координаты точки 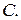 Так как
Так как 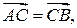 то, согласно части (i), для
то, согласно части (i), для 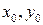 имеем уравнения:
имеем уравнения: 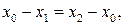
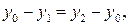 решая которые, получаем нужный результат.
решая которые, получаем нужный результат.
(iii) Поскольку расстояние между точками 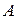 и
и 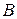 совпадает с длиной вектора
совпадает с длиной вектора 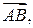 то формула (1) вытекает из первой формулы (4) в § 1.1.5)
то формула (1) вытекает из первой формулы (4) в § 1.1.5)
Разумеется, утверждение 2.1.1, относящееся к плоскости, имеет очевидные аналоги для прямой и пространства.
Далее подобно тому, как это было сделано для векторов в § 1.8.1, получим формулы преобразования координат точек при переходе от одного репера к другому. Как и в случае векторов, вид формул и их вывод одинаков для прямой, плоскости и пространства. Проведем рассуждения для случая плоскости.
Пусть 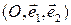 и
и 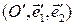 – два аффинных репера на плоскости
– два аффинных репера на плоскости 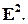 векторов плоскости. Первый из них будем условно называть старым, а второй – новым. Пусть
векторов плоскости. Первый из них будем условно называть старым, а второй – новым. Пусть 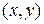 и
и 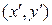 – соответственно старые и новые координаты произвольной точки
– соответственно старые и новые координаты произвольной точки 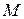 плоскости. Обозначим
плоскости. Обозначим 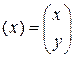 и
и 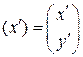 соответствующие координатные столбцы. Нам понадобится матрица перехода
соответствующие координатные столбцы. Нам понадобится матрица перехода 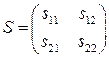 от базиса
от базиса 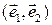 к базису
к базису  и координаты
и координаты 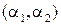 точки
точки 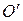 в старом репере. Обозначим
в старом репере. Обозначим 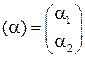 координатный столбец точки
координатный столбец точки 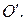 Запишем для точек
Запишем для точек 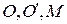 равенство треугольника:
равенство треугольника:
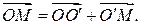 (1)
(1)
Таким же равенством связаны координатные столбцы векторов в старом базисе 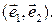 Координатные столбцы радиус-векторов
Координатные столбцы радиус-векторов 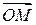 и
и 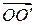 совпадают с координатными столбцами точек, т. е. соответственно с
совпадают с координатными столбцами точек, т. е. соответственно с 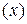 и
и 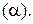 Для вектора
Для вектора 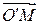 нам также известен координатный столбец
нам также известен координатный столбец 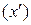 , но только в новом базисе
, но только в новом базисе  По формулам (3) преобразования координат векторов из § 1.1.8 находим координатный столбец вектора
По формулам (3) преобразования координат векторов из § 1.1.8 находим координатный столбец вектора 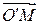 в старом базисе:
в старом базисе: 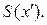 Таким образом,
Таким образом, 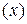 =
= 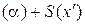 – координатный аналог равенства (1). Окончательно, получаем следующие формулы преобразования координат точек при переходе от одного репера к другому:
– координатный аналог равенства (1). Окончательно, получаем следующие формулы преобразования координат точек при переходе от одного репера к другому:
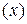 =
= 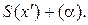 (2)
(2)
В развернутом виде соответственно для прямой, плоскости и пространства:
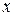 =
= 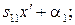
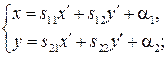
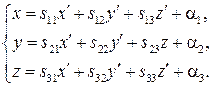
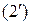
Здесь старые координаты 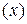 произвольной точки выражены через ее новые координаты
произвольной точки выражены через ее новые координаты 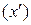 с помощью матрицы перехода
с помощью матрицы перехода 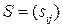 и координат
и координат 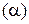 нового начала координат в старом репере.
нового начала координат в старом репере.
Рассмотрим подробнее формулы преобразования прямоугольных координат на плоскости. Пусть 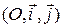 и
и 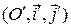 – два ортонормированных репера на плоскости
– два ортонормированных репера на плоскости 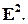 Если
Если 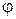 – величина угла между векторами
– величина угла между векторами 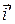 и
и 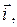 то
то 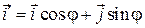 (рис 7). Аналогично, если
(рис 7). Аналогично, если 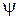 – величина угла между векторами
– величина угла между векторами 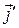 и
и 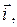 то
то  Числа
Числа 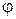 и
и 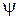 связаны между собой. Если базисы
связаны между собой. Если базисы 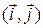 и
и 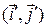 одинаково ориентированы, то
одинаково ориентированы, то 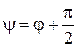 (рис. 7), если же базисы
(рис. 7), если же базисы 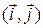 и
и 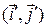 имеют противоположную ориентацию, то
имеют противоположную ориентацию, то 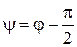 (рис. 8).
(рис. 8).

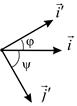
Рис. 7 Рис. 8
Следовательно, 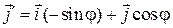 в первом случае и
в первом случае и 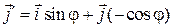 во втором. Таким образом, формулы преобразования координат точек на плоскости при переходе от прямоугольной системы координат
во втором. Таким образом, формулы преобразования координат точек на плоскости при переходе от прямоугольной системы координат 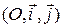 к прямоугольной системе координат
к прямоугольной системе координат 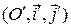 имеют вид:
имеют вид:
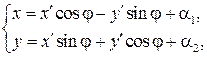 если
если 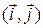 и
и 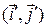 одинаково ориентированы, либо
одинаково ориентированы, либо
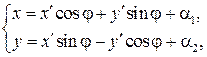 если
если 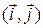 и
и 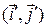 противоположно ориентированы.
противоположно ориентированы.
В частности,
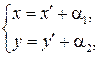 – формулы преобразования координат при параллельном переносе системы координат на вектор
– формулы преобразования координат при параллельном переносе системы координат на вектор 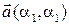 , а
, а
 – формулы преобразования координат при повороте прямоугольной системы координат вокруг точки
– формулы преобразования координат при повороте прямоугольной системы координат вокруг точки  на угол
на угол 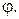
| <== предыдущая страница | | | следующая страница ==> |
| Категория падежа и функционально-семантические поля | | | ФИГУРЫ И ИХ УРАВНЕНИЯ |
Дата добавления: 2014-11-15; просмотров: 553; Нарушение авторских прав

Мы поможем в написании ваших работ!