ФИГУРЫ И ИХ УРАВНЕНИЯ

Будем называть фигурой произвольное множество точек 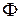в пространстве, на плоскости или на прямой. Аналитическая геометрия изучает фигуры, используя метод координат. Его суть заключается в том, что фиксируя некоторую систему координат, точки заменяют их координатами и задают фигуру как множество решений уравнения (системы уравнений) или неравенства (системы неравенств). Далее уравнения или неравенства анализируют методами алгебры и результаты анализа интерпретируют геометрически как свойства фигуры. Задание фигур с помощью уравнений или неравенств используют и в средней школе. Известно, например, что уравнение 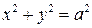задает в прямоугольной системе координат 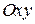на плоскости окружность 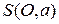с центром в точке и радиуса 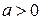а неравенство 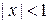задает на координатной оси 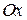открытый интервал.

Далее речь пойдет о фигурах на плоскости 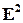и способах их задания. Читателю рекомендуется в качестве упражнения сформулировать соответствующие определения и утверждения для фигур на прямой и в пространстве.

Определение 2.1.1. Пусть 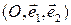– аффинный репер на плоскости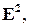 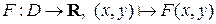– вещественнозначная функция двух аргументов, заданная на подмножестве 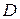множества 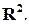Будем говорить, что уравнение

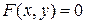(1)

является уравнением фигуры 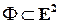в данном репере, если множество решений уравнения (1) совпадает с множеством координат точек фигуры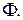

Другими словами, уравнение (1) является уравнением фигуры в репере 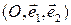, если эта фигура может быть определена следующим образом:

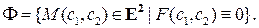
Если 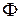имеет уравнение (1), то говорят также, что фигура 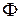заданаэтим уравнением.

Для нахождения уравнения фигуры в данном репере следует для произвольной точки плоскости 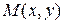через ее координаты 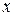и 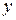записать характеристическое свойство этой фигуры, т.е. условие, которому удовлетворяют точки фигуры и только они. Например, для окружности 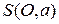таким свойством является условие: расстояние от точки 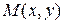до центра окружности равно 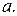В прямоугольных координатах это условие записывается следующим образом: 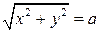или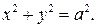

Зная уравнение (1) фигуры 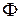в данном репере 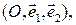можно найти уравнение этой фигуры в любом другом репере 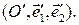Для этого воспользуемся формулами преобразования координат (2) из § 2.1:

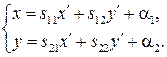
Подставляя в уравнение (1) выражения 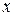и 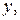получим искомое уравнение:

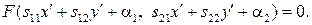
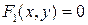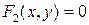Отметим также следующий очевидный факт. Если и – уравнения фигур соответственно 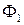и 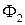в репере 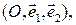то пересечение 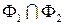задается в данном репере системой уравнений

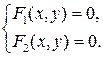
Наряду с заданием фигур с помощью уравнений используется также параметрическое заданиефигур.

Определение 2.1.2. Пусть 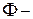фигура на плоскости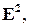 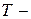некоторое множество, элементы которого будем называть параметрами. Сюръективное отображение

(2)

называется параметризациейфигуры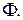

Например, пусть 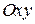– прямоугольная система координат на плоскости 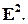Рассмотрим отображение 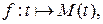ставящее в соответствие числ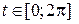у точку 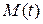на плоскости, находящуюся на расстоянии 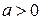от точки и такую, что величина угла поворота вектора 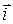до вектор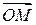а равна 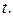Очевидно, что 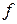– параметризация окружности 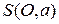(рис. 9).

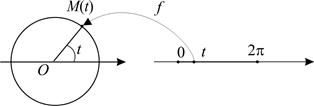
Рис. 9

При параметрическом задании каждому значению 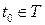параметра 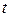отвечает точка 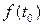фигуры 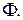Параметризацию можно рассматривать, как математическое обобщение физической ситуации, когда траектория движения точки (фигура 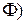описывается в зависимости от времени (параметра

В аналитической геометрии часто встречаютсядве вариации параметризации, а именно, векторно-параметрическое и координатно-параметрическое задание фигур. Первая из них возникает, если зафиксировать точку 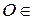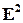и, используя биекцию 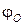(см. замечание 2.1.1), множество 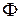точек фигуры заменить множеством 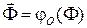их радиус-векторов.

Определение 2.1.3. Векторно-параметрическим заданием фигуры 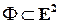называется сюръективное отображение

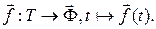(3)

Понятно, что биекция 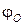позволяет переходить от отображения (3) к отображению (2) и наоборот.

Пусть теперь 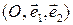– аффинный репер на плоскост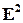и и 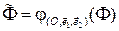множество координат точек фигуры 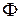(см. замечание 2.1.1).

Определение 2.1.4. Координатно-параметрическим заданием фигуры 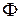называется сюръективное отображение

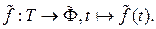(4)

И вновь, используя биекцию 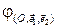, можно переходить от отображения (4) к отображению (2) и наоборот.

Для упоминавшейся выше окружности 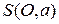укажем векторно-параметрическое задание:

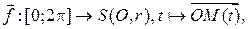
и координатно-параметрическое задание:

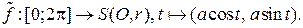
В математике наряду с декартовыми используют и другие системы координат. Чаще всего встречаются полярная система координат на плоскости и сферическая система координат в пространстве.

Для задания полярной системы координат надо зафиксировать на плоскости 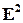точку О,называемую полюсом, выбрать луч 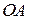с вершиной в точке О, который называется полярным лучом, и одно из двух возможных направлений вращения на плоскости вокруг точки О, которое считается положительным (рис. 10).

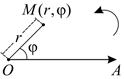
Рис. 10 Рис. 11

Если М – произвольная точка плоскости, отличная от полюса, то полярные координаты этой точки – это пара чисел 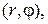которые называются соответственно полярным радиусом и полярным углом точки М. Здесь 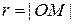– расстояние от точки М до полюса, а 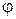– величина угла, на который надо повернуть полярный луч вокруг полюса для того, чтобы он совместился с отрезком ОМ. При этом величины углов поворотов в положительном направлении считаются положительными, а в противоположном направлении – отрицательными. 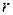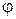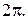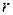Число для точки М определяется однозначно, а – с точностью до целых кратных Для полюса полярный радиус равен 0, полярный угол 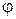не определен. Если наряду с полярной системой координат на плоскости рассмотреть согласованную с ней декартову прямоугольную систему координат (начало декартовой системы координат совпадает с полюсом; положительный луч оси Ох совпадает с полярным лучом; при повороте на 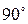в положительном направлении полярный луч совпадает с положительным лучом оси Оу, рис. 11), то полярные 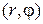и декартовы 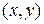координаты одной и той же точки связаны между собой формулами:

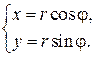
Некоторые фигуры на плоскости удобно задавать уравнениями в полярной системе координат, например, полярное уравнение окружности 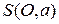имеет вид: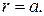

Для задания сферической системы координат надо зафиксировать в пространстве 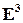плоскость 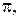на ней выбрать точку О, луч 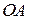с вершиной в точке О и одно из двух возможных направлений вращения на плоскости 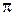вокруг точки О, которое считается положительным. Кроме того, следует выбрать одно из двух полупространств, определяемых плоскостью 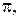которое считается положительным, другое подпространство считается отрицательным. Обозначим прямую, проходящую через точку О перпендикулярно плоскости 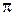(рис. 12).

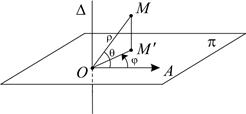
Рис. 12

Пусть М – произвольная точка пространства, не лежащая на прямой 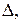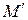– ортогональная проекция точки М на плоскость 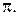Сферические координаты точки М – это тройка чисел 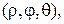которые определяются следующим образом. Число 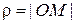– расстояние от точки М до точки О, число 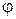– величина угла, на который надо повернуть луч 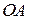в плоскости 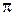вокруг точки О для того, чтобы он совместился с отрезком 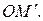При этом величины углов поворотов в положительном направлении считаются положительными, а в противоположном направлении – отрицательными. 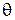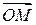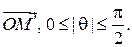Число по модулю равно величине угла между векторами и Если т. 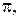е точка М не лежит в плоскости то 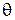положительно для точек М положительного полупространства и отрицательно для точек М отрицательного полупространства. 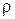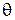Для указанной точки М числа и определяются однозначно, число 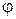– с точностью до целых кратных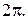

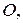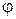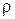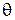Если точка М лежит на прямой и не совпадает с точкой то для нее число не определяется, а числа и определяются следующим образом: 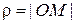, 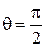для точек положительного полупространства, 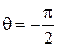для точек отрицательного полупространства. Для точки число 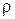считается равным 0, числа 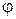и 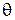не определены.

Обычно наряду со сферической системой координат в пространстве рассматривают согласованную с ней декартову прямоугольную систему координат 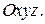Согласованность систем координат означает, что начало декартовой системы координат совпадает с точкой ; плоскость 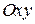совпадает с плоскостью 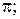положительный луч оси Ох совпадает с лучом 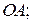при повороте на 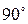в положительном направлении луч 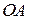совпадает с положительным лучом оси Оу; положительным полупространством считается полупространство, состоящее из точек с положительными аппликатами. В таком случае сферические и декартовы координаты одной и той же точки связаны между собой формулами:

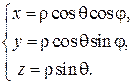
Сферические координаты иногда называют еще географическими координатами, в этом случае число 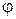называется долготой точки М, число 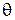– широтой точки М. Эти названия объясняются тем обстоятельством, что для точек земного шара географические долгота и широта определяются соответственно как 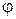и 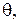если принять следующие соглашения: в качестве плоскости 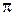взять плоскость экватора; считать, что точки северного полушария лежат в положительным полупространстве, точки южного полушария лежат в отрицательном полупространстве; отсчитывать угол 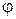от гринвичского (нулевого) меридиана.

Дата добавления: 2014-11-15; просмотров: 886; Нарушение авторских прав

Мы поможем в написании ваших работ!