Инвертирование представлений

В силу многих обстоятельств современному пользователю систем управления проектами требуется одинаково свободно владеть обоими вышеописанными представлениями (обоими типами AoA и AoN). Лучшим доказательством того, что оба представления понятны, является возможность построения инвертированного представления к исходному.

Рассмотрим сначала преобразование ПЕРТ-графа к Гант-графу на примере (рисунок 2.2-6). Слева приведен пример классического представления сетевого графика, а справа полученное из него инвертированное представление.

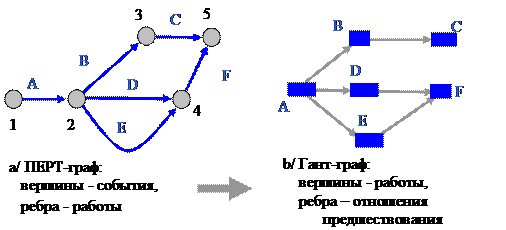
Рисунок 2.2‑6. Преобразование ПЕРТ-графа к ГАНТ-графу .

Если инвертированное представление после приведенного примера осталось непонятным, попробуйте повторить следующую механическую процедуру построения инвертированного представления:

ü образуйте (нарисуйте) вершины Гант-графа (каждая вершина – работа) и промаркируйте их названием (идентификатором) работы;

ü проанализируйте все пары инцидентных ребер (работ) ПЕРТ-графа; если одно ребро в паре является входящим, а другое исходящим, то такой паре должно соответствовать ребро в Гант-графе (с очевидным направлением).

А теперь посмотрим как по исходному Гант-графу (рисунок 2.2-7a) был построен ПЕРТ-граф (рисунок 2.2-7b). представления сетевого графика, а справа полученное из него инвертированное представление.

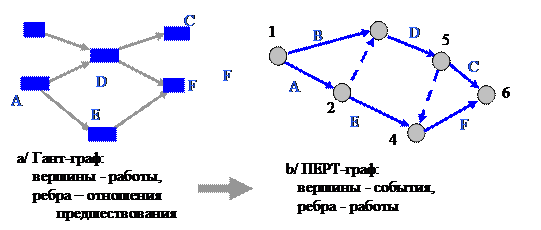
Рисунок 2.2‑7. Преобразование ГАНТ-графа к ПЕРТ -графу .

Формальный алгоритм для проведения подобного преобразования достаточно сложен. Поэтому попробуем обойтись объяснением проведенного преобразования на данном примере.

Построение ПЕРТ-представления начнем с события 1 – начало проекта. На Гант-представлении видно, что лишь две вершины A и B являются корневыми (не имеют входящих ребер). Из этого следует что на ПЕРТ-представлении из вершины 1 (событие-старт проекта) исходит два ребра (две работы): A и B. Добавим эти ребра и обозначим их конечные вершины через 2 и 3, соответственно. Заметим, что объединить два события 2 и 3 в одно нельзя, ибо событие 2 имеет самостоятельное значение – именно после его наступления можно начать работу E. Получаем начальный фрагмент инвертированного представления приведенный на рисунке 2.2-8a.

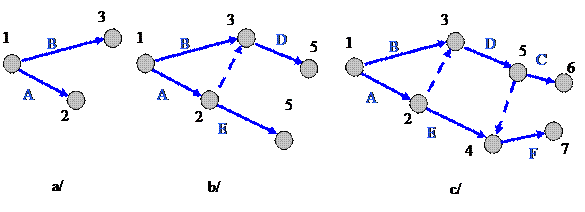
Рисунок 2.2‑8. Последовательные иллюстрации к преобразованию ГАНТ-> ПЕРТ.

Изобразим теперь ребро (работу) E, предшественником которого должно быть ребро A, и, следовательно, ребро E является исходящим из вершины 2.

У работы D два предшественника: A и B. Поскольку, как уже отмечалось, объединить два события 2 и 3 в одно нельзя, то остается единственный вариант: определить ребро D исходящим из вершины 3 и добавить фиктивную работу 2->3. Получаем фрагмент инвертированного представления приведенный на рисунке 2.2-8b. Объединить два события 4 и 5 в одно нельзя, ибо событие 5 имеет самостоятельное значение – именно после его наступления можно начать работу С.

Работа С, предшественником которого должно быть ребро D, добавляется исходящим из вершины 5.

У работы F два предшественника: D и E. Поскольку объединить два события 4 и 5 в одно нельзя, то остается добавляем ребро F исходящим из вершины 4 и добавить фиктивную работу 5->4. Получаем фрагмент инвертированного представления приведенный на рисунке 2.2-8с.

Для получения результирующего результата преобразования приведенного на рисунке 2.2-7b осталось объединить вершины не имеющих исходящих ребер в одну вершину – событие окончания проекта.

2.2.2 Сетевой график и календарное планирование

Рассмотренная в предыдущем разделе модель сетевого графика не дает ответ на задачу календарного планирования – когда должна начаться каждая из задач проекта, какие ресурсы и когда должны привлекаться. Для того чтобы наделить сетевой график такими возможностями необходимо лишь привязать сетевой график к временной шкале и определить ресурсы потребные для исполнения каждой из представленных в графике работ. Сетевые графики наделенные такими свойствами называют календарными сетевыми графиками.

Для привязки сетевого графика к временной шкале основополагающим является выбор типа привязки. Различаются два типа проектов:

ü c заданной датой начала проекта,

ü с заданной датой окончания проекта.

В проектах с заданной датой начала каждую работу начинают как можно быстрее. В проектах с заданной датой начала проекта каждую работу начинают как можно позже. Объясняется это обстоятельство лишь одним – необходимо минимизировать срок окупаемости путем скорейшего окончания проекта (в проекте с заданной датой начала) либо путем максимально поздних затрат (в проекте с заданной датой окончания).

Итак, для привязки сетевого графика к временной оси достаточно указать тип проекта и соответствующую дату начала или окончания проекта. Дата начала и окончания каждой работы после этого становится детерминированной (вычисляемой). Возможные вариации этих вычислений рассматриваются в следующем разделе.

Назначение ресурсов (людских и финансовых ресурсов, оборудования, расходных материалов) потребных для исполнения каждой задачи в совокупности с определенными сроками исполнения работ не только позволяет рассчитать календарные графики использования ресурсов, но и ставит еще одну расчетную задачу перед менеджером проекта. В условиях ограниченных ресурсов необходимо осуществлять контроль за тем, чтобы в любой момент исполнения проекта суммарное количество каждого используемого в этот момент ресурса не превысило установленное ограничение. Процесс такого контроля, включающий средства изменения сроков исполнения работ и переброски ресурсов как средства борьбы с обнаруженными нарушениями, называется выравниванием ресурсов (resource leveling).

Дата добавления: 2014-11-15; просмотров: 297; Нарушение авторских прав

Мы поможем в написании ваших работ!