
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Динамика вращательного движения материальной точки
Пример с равномерным движением одной и двух М.Т. по окружности показывает, что динамические характеристики поступательного движения непригодны для описания вращательного движения М.Т.
Момент импульса материальной точки относительно точки
Моментом импульса материальной точки относительно некоторой точки О называется векторное произведение радиус-вектора r, проведенного из точки О к материальной точке и вектора импульса М.Т. p : 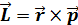 . Согласно правилу векторного перемножения двух векторов результирующий вектор направлен по нормали к плоскости, в которой лежат эти вектора и по величине равен площади параллелограмма, составленного из этих двух векторов.
. Согласно правилу векторного перемножения двух векторов результирующий вектор направлен по нормали к плоскости, в которой лежат эти вектора и по величине равен площади параллелограмма, составленного из этих двух векторов.
Момент cилы материальной точки относительно точки
Момент силы материальной точки относительно точки определяется аналогичным образом: 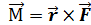
Связь между моментом импульса и моментом силы материальной точки
определяется через производную от момента импульса по времени: 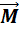 =
= 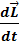
Это основное уравнение динамики вращательного движения материальной точки
ЗАКОН ИЗМЕНЕНИЯ И СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
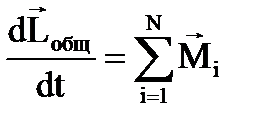 Рассмотрим систему материальных точек, которые взаимодействуют меж собой и подвержены воздействию извне. Результирующий момент сил, действующих на систему материальных точек, равен сумме моментов сил, действующих на отдельные точки. Общий момент сил внутреннего попарного взаимодействия равен нулю, поэтому изменение полного момента импульса системы материальных точек определяется только результирующим моментом внешних сил.
Рассмотрим систему материальных точек, которые взаимодействуют меж собой и подвержены воздействию извне. Результирующий момент сил, действующих на систему материальных точек, равен сумме моментов сил, действующих на отдельные точки. Общий момент сил внутреннего попарного взаимодействия равен нулю, поэтому изменение полного момента импульса системы материальных точек определяется только результирующим моментом внешних сил.
Если система материальных точек является замкнутой, то полный момент
импульса остается неизменным.
Момент импульса материальной точки относительно оси
Имеется существенное различие между понятиями момент импульса относительно материальной точки и относительно оси. Проекция момента импульса материальной точки относительно любой точки, лежащей на оси вращения, одинакова и обозначается как Lzo . Это и есть момент импульса материальной точки относительно оси. Если момент импульса материальной точки относительно точки является векторной величиной, то момент импульса относительно оси – это проекция на ось его момента относительно точки, лежащей на оси. Таким образом, момент импульса относительно оси уже не является векторной величиной.
Лекция №7
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Вращательное движение твердого тела относительно неподвижной оси
Момент импульса твердого тела, вращающегося относительно неподвижной оси, можно представить как сумму моментов отдельных материальных точек, его составляющих. Поскольку всеDLi направлены вдоль оси вращения, суммарный момент импульса материальных точек твердого тела есть арифметическая суммаDLi
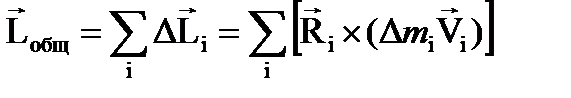
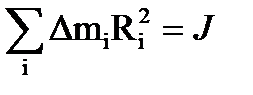 Переходя к угловой скорости вращения, одинаковой для всех DLi , получим:
Переходя к угловой скорости вращения, одинаковой для всех DLi , получим:
- 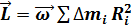 момент инерции.
момент инерции.
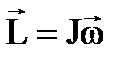 Момент инерции служит мерой инертности твердого тела при вращательном движении, поскольку в данном случае инертность тела определяется не только его массой, но и ее распределением относительно оси вращения.
Момент инерции служит мерой инертности твердого тела при вращательном движении, поскольку в данном случае инертность тела определяется не только его массой, но и ее распределением относительно оси вращения.
- Связь момента импульса с моментом инерции
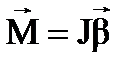
ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Как и в случае системы материальных точек для твердого тела, на которое не действуют внешние силы, момент импульса остается неизменным во времени 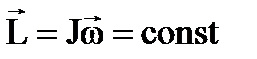
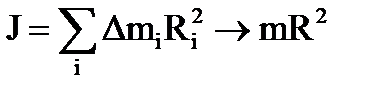 Моменты инерции различных по форме тел
Моменты инерции различных по форме тел
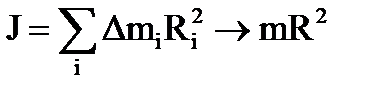 материальная точка
материальная точка
Тонкостенный цилиндр
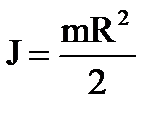
Сплошной цилиндр или диск
Момент инерции стержня относительно оси, проходящей через его центр
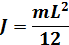
Момент инерции шара относительно оси, проходящей через его центр 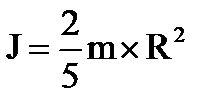
ТЕОРЕМА ШТЕЙНЕРА. Теорема Штейнера устанавливает связь между моментом инерции твердого тела относительно оси, проходящей через центр масс, и любой другой осью, параллельной исходной 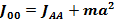
Момент инерции твердого тела относительно произвольной оси равен моменту инерции этого тела относительно оси, параллельной исходной, плюс произведение массы тела на квадрат расстояния между осями.
Примечание. Поскольку момент инерции J зависит как от массы, так и ее распределения относительно оси вращения, то J изменяется не только при смещении тела, но и его повороте относительно оси вращения.
РАБОТА И ЭНЕРГИЯ ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
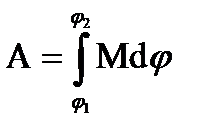 Работа, совершаемая при вращательном движении твердого тела относительно
Работа, совершаемая при вращательном движении твердого тела относительно
неподвижной оси:
Кинетическая энергия твердого тела при вращательном движении относительно
неподвижной оси 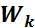 =
= 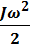
Если тело участвует одновременно во вращательном и поступательном движениях, то кинетическая энергия тела равна сумме энергии поступательного и вращательного движения:
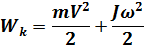
| <== предыдущая страница | | | следующая страница ==> |
| ЭНЕРГИЯ | | | Лекция №8 ЭЛЕКТРОСТАТИКА |
Дата добавления: 2014-11-24; просмотров: 411; Нарушение авторских прав

Мы поможем в написании ваших работ!