ЭНЕРГИЯ

Энергия- это скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Понятие об энергии в естествознании имеет широкий смысл - это кинетическая и потенциальная энергия, внутренняя и свободная энергия, энергия связи, энергия химической и ядерной реакции, энергия покоя, энергия электромагнитного поля, лучистая энергия, тепловая энергия.

Кинетическая и потенциальная энергия

Понятие о кинетической и потенциальной энергии рассмотрим на примере бруска на наклонной плоскости.

Исходное положение I у основания наклонной плоскости, конечное II – верхней точке наклонной плоскости. В отсутствии трения работа по подъему бруска по наклонной плоскости из I в II: A=F·S=mgsina·S=mgh. При свободном движении вниз та же сила совершает работу, приводя к изменению из состояния покоя бруска к состоянию движения. Выражение для работы в терминах скорости бруска (V²=2aS) имеет вид: A=F·S=mg·sina·S= 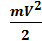. 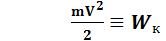- это кинетическая энергия.

Работа силы по перемещению тела равна приращению его кинетической энергии.

Общий формальный подход .

Преобразуем выражение для работы: d )=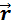

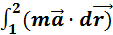
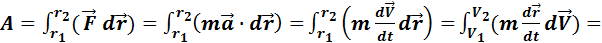
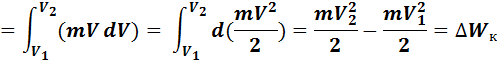
К системе брусок – наклонная плоскость добавим груз, связанный с бруском веревкой, перекинутой через блок. Брусок при переходе из положения I в положение II совершает работу, поднимая груз на высоту h. Другими словами в положении II брусок m обладает способностью совершать работу, т.е. обладает энергией, которая носит название ПОТЕНЦИАЛЬНОЙ. Работа, связанная с подъемом груза m_i на высоту h, совершаемая бруском m при переходе из положения II в положение I, лишает его возможности совершать работу, т.е. приводит к убыли его потенциальной энергии. Отсюда А= -DW_п. Работа равна убыли потенциальной энергии.

Связь силы и потенциальной энергии

В дифференциальной форме: dA= -dW_п.

Потенциальная энергия в общем случае является функцией координат: W_п(x,y,z) и ее полный дифференциал имеет вид: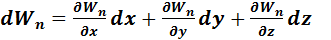

Cравним это выражение с выражением для элементарной работы

dA= F_xdx + F_ydy + F_zdz

откуда Fx=-∂Wn/∂x Fy=-∂Wn/∂y Fz=-∂Wn/∂z

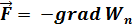
Потенциальные и непотенциальные силы

Рассмотрим другой пример -перемещение бруска по горизонтальной поверхности при наличии силы трения. При перемещении бруска из положения I в положение II совершается работа против

силы трения. Однако, в данном случае брусок самопроизвольно не возвращается в исходное положение I после прекращения внешнего воздействия. Такая ситуация существенным образом отличается от перемещения бруска m_i под действием силы тяжести, когда после прекращения внешнего брусок самопроизвольно возвращается в исходное положение. Различие в этих двух примерах состоит в том, что сила тяжести является консервативной, а сила трения - неконсервативной. Консервативной называется сила, работа которой не зависит от формы пути, а определяется начальной и конечной точками движения.

Величина потенциальной энергии может быть определена с точностью до const, выбор которой зависит от начала отсчета.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ РАЗЛИЧНЫХ СИЛ ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И ЗАКОН ЕЕ СОХРАНЕНИЯ

Потенциальная энергия различных сил определяется на основании выражения для работы этих сил и соотношения А= W_n1-W_n2

Потенциальная энергия силы тяжести: W_n(z)=mgz+ const const→0

Потенциальная энергия силы упругости: W_n =kx²/2+ const const→0

Потенциальная энергия силы кулоновского взаимодействия точечных зарядов:

W_n = kq₁q₂/r+ const const→0

Величина потенциальной энергии до некоторой степени произвольна и зависит от выбора начала отсчета, а также значения потенциальной энергии в этой точке.

Однозначно определенной величиной является лишь разность потенциальной энергии начального и конечного положения тела, определяемая через работу консервативных сил по перемещению тела из конечного в начальное положение.

Полная механическая энергия

Связь между работой и кинетической энергией определяется соотношениями:

А=W_K2- W_K1 и А= W_n1- W_n2. Приравняем правые части этих выражений:

W_K2- W_K1 = W_n1- W_n2

Перенесем в одну сторону величины с одинаковыми индексами: W_K2+ W_n2= W_n1+ W_K1

Поскольку начальная (I) и конечная (2) точки перемещения тела могут быть выбраны произвольно, то величина W_K+ W_n остается неизменной. Сумма кинетической и потенциальной энергии носит название полной механической энергии W_K+ W_n =W _полн

Закон сохранения механической энергии: В системе тел, где действуют только консервативные силы, полная механическая остается постоянной.

Лекция №6

Дата добавления: 2014-11-24; просмотров: 264; Нарушение авторских прав

Мы поможем в написании ваших работ!