
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ДИНАМИКА
ЗАКОНЫ НЬЮТОНА
Первый закон Ньютона
КЛЮЧЕВЫЕ ЭКСПЕРИМЕНТЫ
Эксперимент №1 Человек и брусок на горизонтальной поверхности
К бруску, лежащему неподвижно, подходит человек и с помощью веревки перемещает брусок по поверхности. По окончанию воздействия человека брусок останавливается.
Интерпретация этих результатов, данная еще Аристотелем: Сила является источником движения. С прекращением действия силы прекращается движение.
Эксперимент №2 Брусок, скатывающийся с наклонной плоскости
Основное отличие от предыдущего эксперимента: на горизонтальном участке пути брусок продолжает движение, хотя, как и ранее, на него не оказывается никакого внешнего воздействия. На этом участке пути тела движутся равнозамедленно . Степень замедления не зависит от свойств наклонного участка пути, а определяется трением между движущимся телом и поверхностью.
Интерпретация результатов эксперимента: на горизонтальном участке пути тела стремятся двигаться равномерно, причиной замедления движения является ТРЕНИЕ .
Эксперименты №5 и 6 Свободное падение тел. Тяжелое и легкое тело падают с одинаковой высоты. На воздухе тяжелые тела падают быстрее легких тел. Повторение эксперимента, но уже в вакууме показало, что эти тела движутся одинаковым образом.
Интерпретация результатов эксперимента: все тела подвержены притяжению Земли, воздух оказывает сопротивление движению тел, поэтому легкие и тяжелые тела падают по- разному.
Таким образом, на горизонтальном участке пути как на брусок, так и на шарик действует притяжение со стороны Земли, которое направлено вертикально. Возникает вопрос: имеются ли другого рода воздействия в вертикальном направлении на тела, движущиеся по горизонтальной поверхности?
Воздействия, испытываемые телами в вертикальном направлении.
Эксперимент №7 с платформой на пружинах показал, что на тела помимо притяжения Земли действует реакция опоры, направленная вертикально вверх. Эти два воздействия компенсируют друг друга, что обеспечивает отсутствие движения в вертикальном направлении.
Характер движения в горизонтальном направлении: С одной стороны - отсутствие движения в отсутствии внешнего воздействия, а с другой - стремление к сохранению равномерного и прямолинейного характера движения, чему препятствует трение.
ФОРМУЛИРОВКА 1-ого ЗАКОНА НЬЮТОНА:
Тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока отсутствует внешнее воздействие или оно скомпенсировано.
Свойства тел сохранять состояние покоя или равномерного и прямолинейного движения называется ИНЕРЦИЕЙ. Мерой инертности тела является МАССА.
Инерциальные системы отсчета
Системы отсчета, в которых выполняется 1-ый закон Ньютона, называются инерциальными.
Поскольку 1-ый закон Ньютона уравнивает состояние покоя и равномерного, прямолинейного движения, то любая система координат, движущаяся равномерно и прямолинейно относительно инерциальной также является инерциальной.
Принцип относительности Галилея
Все физические явления проистекают одинаковым образом во всех инерциальных системах отсчета
Пример: Стрельба по мишеням на корабле, который движется равномерно и прямолинейно относительно берега. Один стрелок стоит на корме, а другой на носу. Оба стреляют одновременно из одинакового оружия. Вопрос: чья пуля раньше поразит мишень?
Решение этой задачи в системе координат на берегу является достаточно громоздким. Решение этой задачи в системе координат на палубе корабля тривиально – стрелки неподвижны, выстрелы производятся одновременно, скорости пуль одинаковы. И в том и другом случае расчет показывает, что мишени будут поражены одновременно.
Из принципа относительности Галилея следует, что на основании законов движения тел невозможно выделить какую либо инерциальную систему отсчета среди других.
Примечание: в неинерциальных системах отсчета этот принцип неприменим.
Примеры: стрельба на корабле, который движется с ускорением и торможение трамвая с пассажиром и шаром.
Преобразования Галилея
Постановка задачи: Имеется материальная точка, неподвижная относительно инерциальной системы координат. Вторая система координат движется относительно первой в положительном направлении оси Х со скоростью Vo. Тогда преобразование координат, скоростей и ускорений
имеет вид: х2=х1-Vot V2x=V1x-Vo а2х=а1х
y2=y1 , V2y=V1y а2у=а1у
z2=z1; V2z=V1z а2z=а1z
2-ой закон Ньютона
Два фундаментальных понятия в динамике – масса и сила
МАССА
Понятие о массе имеет несколько аспектов
МАССА как мера количества вещества
Обыденное или «житейское» определение массы - это количество вещества. Из определения самого Ньютона: Масса- это количество материи пропорциональное плотности и объему тела.
Согласно этой концепции массу тела можно определить, используя эталонную массу и невесомый стержень, закрепленный на оси вращения.
МАССА как мера инертности
Опыты с брусками, находящимися на горизонтальной поверхности и пружиной, зажатой между ними. Скорости, которые приобретают бруски после распрямления пружины, обратно пропорциональны их массам: V1:V2=m2:m1 или m1V1=m2V2
Вывод: Тела с большей массой в большей степени препятствуют изменению своего состояния.
Движение тел переменной массы
Схема эксперимента: тележка с сыпучим материалом, блок, груз, тянущий тележку. Если масса тележки остается неизменной, то она движется с постоянным ускорением. Если содержимое тележки высыпается по мере ее движения, то ускорение тележки растет по мере движения.
Вывод: При одинаковом внешнем воздействии уменьшение массы движущегося тела приводит к уменьшению его инертности.
МАССА как мера гравитационного взаимодействия
Свободное падение тел наЗемле обусловлено гравитацией – свойством тел притягиваться друг к другу. Всеобщий характер гравитационных свойств массы обеспечивает нормальное функционирование человека в любой точке Земли, несмотря на то, что она имеет шарообразную форму.
СИЛА
Сила- это физическая, векторная величина, являющаяся мерой взаимодействия тел
Варианты формулировки 2-ого закона Ньютона
2-ой закон Ньютона устанавливает связь между силой, действующей на тело, его массой и ускорением, с которым оно движется. Возможны разные подходы к формулировке этого закона –поскольку сила и масса не могут быть определены независимо друг от друга
«Школьная» формулировка 2-ого закона.
В качестве исходной величины выступает сила, а масса в виде 1/m является коэффициентом пропорциональности между силой и ускорением: a~F a=F/m
Ускорение, приобретаемое телом, пропорционально действующей силе. Такая формулировка 2-ого закона Ньютона логически ПРОТИВОРЕЧИВА, поскольку величину самой силы предлагается определять через массу, которая выступает в роли коэффициента пропорциональности : 1 Ньютон - это сила, которая массе в 1кг сообщает ускорение в 1м/с2 в направлении действующей силы.
Определение единицы измерения силы путем взвешивания
Этот метод определения единицы измерения силы также имеет свои недостатки, поскольку сила тяжести неодинакова в разных точках на поверхности Земли. Так было условлено производить взвешивание на уровне моря на географической широте 45°. За единицу измерения силы в системе единиц СИ принимается сила, с которой Земля притягивает гирю массой 0,102 кг на вышеуказанной широте. Однако и в этом варианте определения эталона силы опять используется заранее определенная величина массы.
В следующем варианте определения эталона силы предлагается сравнивать величину силы с удлинением пружины. И в этом случае невозможно дать определение единицы измерения силы без единицы измерения массы.
Понятие массы в классической механике является более фундаментальным, нежели силы. Масса наряду с длиной и временем являются основными физическими величинами в классической механике.
2-ой закон Ньютона через импульс
В опыте с брусками и пружиной было показано, что после распрямления пружины абсолютная величина mV одинакова для обоих брусков. Пусть за время распрямления пружины Dt на бруски действовала усредненная по величине сила F . Произведение FDt называется импульсом силы.
Тогда FDt = m1V1 = m2V2 = D(mV) - Импульс силы равен изменению количества движения - формулировка 2-ого закона самим Ньютоном.
Количество движения mV обозначается как р (р = mV ) и называется импульсом тела.
Тогда 2-ой закон Ньютона через импульс имеет вид:
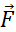 =
= 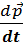
Формулировка 2-ого закона Ньютона в этом виде является предпочтительной по сравнению с F=ma поскольку снимает противоречия между первичностью в определении массы и силы, а также может быть использована для описания движения тел переменной массы:
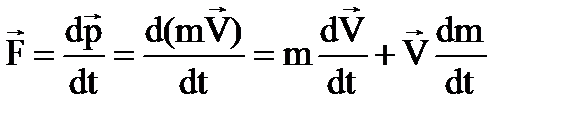
Второе слагаемое в этом выражении отражает факт увеличения ускорения тела при фиксированном значении силы за счет уменьшения массы тела
III-ий закон Ньютона
В инерциальных системах отсчета силы взаимодействия двух тел равны по величине, противоположны по направлению и действуют вдоль прямой, соединяющей тела. Отметим, что наличие двух сил в III законе Ньютона - это удобный математический способ описания взаимодействия тел, поскольку воздействие и противодействие абсолютно равноправны.
Лекция №4
Закон изменения и сохранения полного импульса системы материальных точек
Рассмотрим систему, состоящую из N материальных точек, которые взаимодействуют меж собой и подвержены воздействию извне. Закон изменения импульса i-ой материальной точки:
d 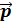 i/dt=
i/dt= 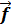 i1+
i1+ 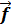 i2+….+
i2+….+ 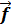 iN+
iN+ 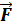 iН
iН
Составим систему из аналогичных уравнений для каждой из М.Т.
Сумма левой части этой системы уравнений представляет производную по времени от полного импульса системы М.Т. : d/dt ( 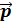 1+
1+ 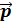 2+…+
2+…+ 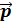 N)= d
N)= d 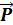 /dt, где
/dt, где 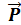 =
= 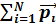
Сумма левой части этой системы уравнений состоит из суммы сил внутреннего попарного взаимодействия ∑ 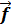 ik и суммы внешних сил ∑
ik и суммы внешних сил ∑ 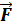 iН=
iН= 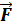 Н. По III закону Ньютона ∑
Н. По III закону Ньютона ∑ 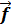 ik =0
ik =0
d 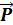 /dt=
/dt= 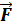 Н - изменение суммарного импульса системы материальных точек обусловлено только результирующим внешним воздействием.
Н - изменение суммарного импульса системы материальных точек обусловлено только результирующим внешним воздействием.
Замкнутой системой материальных точек называется система, которая не испытывает внешнего воздействия (∑ 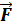 iН= 0).
iН= 0).
Закон сохранения полного импульса системы материальных точек:
d 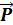 /dt=0 или
/dt=0 или 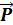 -const.
-const.
В замкнутой системе материальных точек полный импульс остается неизменным.
Это утверждение остается в силе, когда силы внешнего воздействия компенсируют друг друга.
РАБОТА И ЭНЕРГИЯ
РАБОТА
Механическая работа, это скалярная величина, являющаяся мерой результата действия силы, приводящего к перемещению тела или его деформации.
Из школьного курса физики работа по перемещению тела определяется соотношением:
А=F· S cosa. При этом предполагается, что величина силы F и угла a остаются неизменными на всем пути S. Если угол a=0, то геометрическая интерпретация работы – это площадь под графиком зависимости силы F от расстояния S. Если по-прежнему угол a=0, но сила является переменной величиной, то суть геометрической интерпретации работы не меняется. Тогда путь S можно разбить на малые участки DS и считать, что на каждом из этих участков величина силы остается неизменной.
Работа на всем пути S определяется суммой этих элементарных работ и, переходя от суммирования к интегрированию, получим: 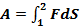
В общем случае, когда направления силы и элементарного перемещения не совпадают:
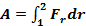 - где Fr – проекция силы на направление элементарного перемещения
- где Fr – проекция силы на направление элементарного перемещения
Выражения для работы некоторых сил
Работа, совершаемая против сил упругости: 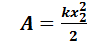 -
- 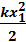
Работа силы кулоновского взаимодействия при движении точечного заряда в поле другого заряда
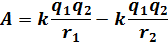
Работа в поле силы тяжести: A=mgh
Лекция №5
| <== предыдущая страница | | | следующая страница ==> |
| Лекция №2 ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ КИНЕМАТИКИ. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ | | | ЭНЕРГИЯ |
Дата добавления: 2014-11-24; просмотров: 247; Нарушение авторских прав

Мы поможем в написании ваших работ!