Динамика. Здесь должно быть задано или заранее определено: положение механизма в данный момент времени (углы j

Задача 3

Здесь должно быть задано или заранее определено: положение механизма в данный момент времени (углы j, a, b, g), кинематические характеристики ведущего звена (w₁, e₁), а также размеры звеньев и положение рассматриваемых точек 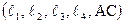. Это позволит найти ускорение всех точек звена 2, совершающего плоское движение, а также движение ведомых звеньев (w₃, e₃, a_D). Для этого сначала определяется ускорение общей точки А 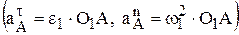и направление (прямые, по которым направлены вектора) ускорений другой общей точки В (учитывается их вращение вокруг неподвижных центров как на рис. 16, либо поступательное движение точки В вместе с ведомым звеном как на рис. 10). Тогда из выражения (7) следует

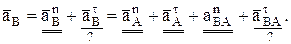(13)

Величины нормальных ускорений 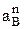вращения точки В вокруг центра О₃ вместе со звеном 3 и 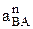– вращения этой точки вокруг полюса А вместе со звеном 2 найдем, используя значения w₂ и w₃, которые определяются через МЦС, как было рассмотрено выше в примере (см. рис. 11), т.е. 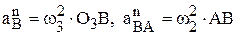. Тогда в векторном уравнении (13) остается две неизвестные и его можно спроецировать на оси Х и Y

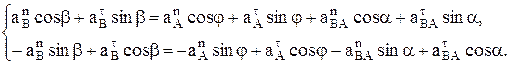(14)

Решая эту систему уравнений можно найти значения двух неизвестных 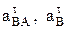, а затем 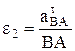и 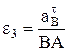. Если значение какого-то касательного ускорения окажется отрицательным, это означает, что правильное направление вектора противоположно первоначально выбранному на рис. 16 (соответственно противоположно направлено соответствующее угловое ускорение e₂ или e₃ ).

Зная w₂ и e₂ , теперь легко найти ускорение любой произвольной точки звена 2, например точки С. Для неё из уравнения (7) следует

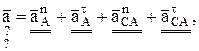(15)

где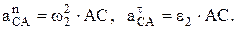

Теперь проецируем (15) на оси

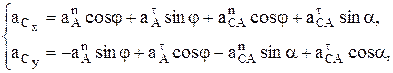(16)

и по проекциям находим модуль, а если необходимо, то и направление вектора .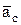

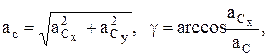(17)

где g – угол вектора с осью Х.

Если в точке С шарнирное соединение с другим звеном CD, совершающим плоскопараллельное движение, то точку С тоже можно взять за полюс и записать

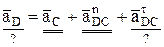. (18)

Последнее векторное уравнение решается аналогично уравнению (13).

Контрольные вопросы:

1. Чем отличаются координатный и естественный способ задания движения точки?

2. Что такое материальная точка?

3. Дать определение относительного, переносного и абсолютного движения точки.

4. Как определяется величина и направление кориолисова ускорения?

5. Определение поступательного движения тела и в чем особенности кинематики этого движения.

6. Как, зная уравнение вращения тела вокруг неподвижной оси, найти величину и направление его угловой скорости ускорения, а также линейную скорость и ускорение произвольной точки тела в любой момент времени?

7. Дать определение плоскопараллельного движения тела, и на какие два движения его можно разложить.

8. Как определить угловую скорость звена и линейные скорости его точек в плоскопараллельном движение через МЦС звена?

9. Как определяются ускорения точек звена, совершающего плоскопараллельное движение?

Динамикой называется раздел теоретической механики, в котором изучается движение тел в зависимости от действующих на них сил. Этот раздел является основным в курсе теоретической механики. Определение «теоретической» означает, что в основу разработки этого раздела положены некоторые теоретические предпосылки называемые аксиомами.

Дата добавления: 2014-02-26; просмотров: 523; Нарушение авторских прав

Мы поможем в написании ваших работ!