
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Модуль 1
Таблица 12 - Исходные данные задачи о четырех видах изделий
| Виды сырья | Технологические коэффициенты | Запасы сырья | |||
| А1 | А2 | А3 | А4 | ||
| I | |||||
| II | |||||
| III | |||||
| Прибыль от реализации | 2,5 |
Требуется, зная решение данной задачи, решить задачу, двойственную ей. Сформулируем исходную ЗЛП. 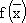 = 6x1 + 2x2 + 2,5x3 + 4x4 → max;
= 6x1 + 2x2 + 2,5x3 + 4x4 → max;
5x1 + x2 + 2x4 ≤ 1000,
4x1 + 2x2 + 2x3 + x4 ≤ 600,
x1 + 2x3 + x4 ≤ 150;
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0.
Оптимальное решение данной задачи состоит в следующем:
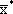 = (0, 225, 0, 150);
= (0, 225, 0, 150); 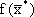 = 1050.
= 1050.
Сформулируем двойственную задачу и решим ее, используя теоремы двойственности. 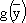 = 1000y1 + 600y2 + 150y3 → min;
= 1000y1 + 600y2 + 150y3 → min;
5y1 + 4y2 + y3 ≥ 6,
y1 + 2y2 ≥ 2,
2y2 + 2y3 ≥ 2,5,
2y1 + y2 + y3 ≥ 4.
y1 ≥ 0, y2 ≥ 0, y3 ≥ 0
Подставим 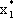 ,
, 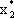 ,
, 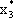 и
и 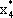 в ограничения исходной задачи:
в ограничения исходной задачи:
5ּ0 + 225 + 2ּ150 < 1000,
4ּ0 + 2ּ225 + 2ּ0 + 150 = 600,
0 + 2ּ0 + 150 = 150
Следовательно, используя вторую теорему двойственности и первое свойство двойственных оценок, можем записать:  = 0.
= 0.
Рассмотрим ограничения двойственной задачи. Каждое их них соответствует одной из переменных исходной задачи. Поскольку 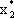 > 0 и
> 0 и 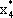 > 0, только второе и четвертое ограничения двойственной задачи обращаются в верное равенство при подстановке в них оптимального плана
> 0, только второе и четвертое ограничения двойственной задачи обращаются в верное равенство при подстановке в них оптимального плана  . Учитывая, что
. Учитывая, что  = 0, можем записать систему из двух уравнений с двумя неизвестными:
= 0, можем записать систему из двух уравнений с двумя неизвестными:
2y2 = 2,
y2 + y3 = 4.
Решая систему, получим: 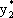 = 1,
= 1, 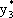 = 3.
= 3.
Полностью решение двойственной задачи запишется так:
 = (0, 1, 3);
= (0, 1, 3); 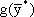 = 1050.
= 1050.
| <== предыдущая страница | | | следующая страница ==> |
| Двойственность в линейном программировании | | | ОБЩАЯ ХАРАКТЕРИСТИКА СПОРТА КАК СОЦИАЛЬНОГО ЯВЛЕНИЯ |
Дата добавления: 2014-02-27; просмотров: 450; Нарушение авторских прав

Мы поможем в написании ваших работ!