Тема 8. Математическое и компьютерное моделирование

Модель – объект или описание объекта, системы для замещения (при определенных условиях, предположениях, гипотезах) одной системы (т.е. оригинала) другой системой для изучения оригинала или воспроизведения его каких-то свойств.

Модель происходит от латинского modulus – образец (можно добавить: кодирования информации на определенном языке или средствами определенного множества символов).

Настоящий период времени характерен настоятельной необходимостью моделирования социально экономических процессов и систем и принятия решений на основе результатов моделирования, ибо такие системы и процессы достаточно сложны, многогранны, динамичны, подвержены случайным воздействиям.

Мир моделей многообразен. Необходимо все многообразие моделей, представить их в виде классификации (способ научной систематизации) – распределить изучаемые объекты по классам (разрядам, отделам) в зависимости от их общих признаков.

Натурное (материальное) моделирование – это моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы, причем между процессами в объекте-оригинале и в модели выполняются некоторые соотношения подобия.

Информационная (абстрактная) модель – это описание объекта на каком либо языке. Абстрактность модели проявляется в том, что ее компонентами являются сигналы и знаки (вернее, заложенный в них смысл), а не физического тела.

Статистические модели – это модели, отображающие объекты в какой-либо момент времени без учета происходящих с ним изменений, как находящиеся в соответствии покоя и равновесия. В них отсутствует временной параметр.

Динамические модели – это модели, описывающие поведение объекта во времени.

Детерминированные модели – это модели, отображающие процессы, в которых отсутствует случайные воздействия.

Вероятностные (стохастические модели) – описание объектов, поведение которых определяется случайными воздействиями (внешними и внутренними); описание вероятностных процессов и событий, характер изменения которых во времени точно предсказать невозможно.

Есть и другие типы моделей.

Основные требования к математической модели:

– наглядность построения модели (используемых гипотез);

– обозримость основных свойств и отношений модели;

– доступность модели для исследования и воспроизведения оригинала;

– сохранение основной информации, содержавшейся в оригинале;

– сжимаемость информации, содержащейся в оригинале;

– получение новой информации, информативность модели;

– адекватность модели (реальной системе) с точностью гипотез;

Жизненный цикл моделируемой системы (решения задач на ЭВМ):

1)сбор информации, выдвижение гипотез и анализ системы;

2)проектирование структуры и состава подмоделей;

3)разработка и отладка отдельных подмоделей, сборка модели;

4)исследование модели: метод, алгоритма (программы) моделирования;

5)исследование адекватности, устойчивости, чувствительности модели;

6)оценка средств моделирования (затраченных ресурсов);

7)установление причинно-следственных связей в исследуемой системе;

8)генерация отчетов и проектных (народно-хозяйственных) решений;

9)модификация модели, возврат к системе с новыми знаниями.

Вычислительный эксперимент (компьютерный эксперимент) – это эксперимент, осуществляемый с помощью модели на ЭВМ с целью определения, прогноза тех или иных состояний системы, реакции на те или иные входные сигналы. Прибором эксперимента здесь является компьютер (и модель!).

Компьютерные технологии достаточно широко распространены в немедицинских исследованиях. Только в области науки, связанные с изучением человека, компьютерные технологии продвигались очень медленно. Однако ситуация меняется на глазах, и электронно-вычислительная техника находит все более широкое применение в медицинских исследованиях.

Моделирование, прогнозирование эпидемий, инфекционных процессов, управление процессом лечения, диагностика болезней и выработка оптимальных стратегий лечения совершенствование известных и разработка новых способов расчёта, диагностики и прогнозирования проведения операций или предварительный расчёт техники операции в медицине является наиболее актуальной научно-практической задачей профессиональной деятельности врача. Использование современных компьютерных и информационных технологий значительно снижает риск совершения ошибки при планировании операции. Компьютерное моделирование очень широко используется при исследовании сложных немеханических систем. Так, например, компьютерное моделирование в медицине позволяет оценить последствия хирургической операции. Такого рода имитационные модели могут использоваться не только в практических целях, но и в образовательных, что имеет огромное педагогическое значение.

Компьютерное моделирование позволяет рассчитать все необходимые параметры и выполнить операцию до того, как она будет сделана в действительности. Если результаты не удовлетворительны, то можно пересчитать параметры и выполнить операцию заново до получения лучших результатов. И теперь операция «на живую» будет выполнена с наилучшими показателями, потому что заранее известно, что надо делать и к чему это приведёт.

Пример 1. Рассмотрим всемирно известную математической модель, в основу которой положена задача о динамике численности популяции.

Пусть x(t) соответствует популяции в момент времени t, где 0<t<T. Через промежуток времени 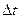она будет равна .

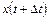Абсолютный прирост равен

.

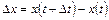Относительный прирост равен

.

Примем гипотезу: необходимые для популяции ресурсы имеются в изобилии и, естественно, скорость роста будет прямо пропорционально размеру популяции т.е. .

Считая , а, также учитывая определение производной, получим из предыдущего соотношения следующее дифференциальное уравнение

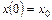, (1)

где 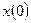– ачальная численность популяции в момент времени t=0, а – остоянная пропорциональности. Величина 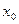считается заданной. Решением задачи (1) является формула экспоненциального роста:

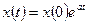
Непрерывной, дифференциальной модели (1) можно поставить в соответствие простую дискретную модель:

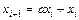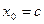, , , (2)

где n предельное значение времени при моделировании.

Эта дискретная модель получается из непрерывной заменой производной 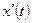на относительное приращение, справедливой при малых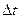

В укрупненных шагах алгоритм моделирования выглядит следующим образом:

1. Ввод входных данных для моделирования;

2. Вычисление 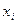от i=1 до i=n по рекуррентной формуле (2);

3. Поиск стационарного состояния т.е. момента времени, начиная с которого все постоянны или изменяются на малую допустимую величину ;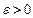

4. Выдача результатов моделирования.

Изложенная выше модель была предложена Мальтусом известным английским демографом в 1798 г. в его классическом труде «О законе роста народонаселения». Томас Роберт Мальтус (1766-1834) – обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно «обгонит» линейную функцию, и наступит голод. На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества. Дарвин обсуждению важности вывода Мальтуса для популяционной динамики посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих лимитирующих факторов среды может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, а также c другими видами, хищничество. Результатом является замедление скорости роста популяции и выход ее численности на стационарный уровень.

Вопросы для самоконтроля

1. Что такое модель, математическая модель, для чего она нужна?

2. Привести типы моделей и определить каждую.

3. Перечислите свойства моделей. Как эти свойства взаимосвязаны?

4. Приведите примеры, убедительно показывающие необходимость каждого из этих свойств.

5. Перечислите основные этапы жизненного цикла моделирования.

6. Что такое вычислительный или компьютерный эксперимент?

7. Перечислите этапы (задачи этапов) компьютерного моделирования.

8. Приведите примеры применения математического и компьютерного моделирования.

Дата добавления: 2014-11-24; просмотров: 509; Нарушение авторских прав

Мы поможем в написании ваших работ!