
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема занятия 11: Резонанс токов
Пассивный параллельный колебательный контур – цепь, в которой элементы L и C подключены параллельно источнику энергии.
Резонанс токов – явление, при котором ток в неразветвленной части минимален. При этом он может быть значительно меньше токов в разветвленных ветвях и совпадать по фазе с входным напряжением.
Условия возникновения резонанса:
1. Параллельное соединение элементов L и C
2. Равенство реактивных проводимостей 
3. Минимальная величина активного сопротивления, обеспечивающего возникновение свободных колебаний в контуре.
Общая проводимость цепи:
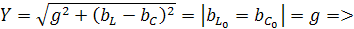
ток и напряжение совпадают по фазе.

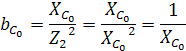
 - реактивные проводимости ветвей.
- реактивные проводимости ветвей.
Частота тока генератора, при котором возникает резонанс токов, определяется из условия равенства реактивных проводимостей параллельных ветвей.


Следовательно, резонансная частота последовательного колебательного контура равна резонансной частоте параллельного колебательного контура.
Резонанс токов наступает тогда, когда частота питающего генератора равна частоте собственных колебаний контура.
Получить резонанс в параллельном контуре можно теми же способами, что и в последовательном колебательном контуре, то есть изменением частоты питающей сети, емкости или индуктивности.
Так как в момент резонанса ток минимален, то
 ,
,
где Q=ρ∕R – добротность контура.
Рассмотрим значения тока в момент резонанса:
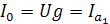 – минимальный общий ток в цепи.
– минимальный общий ток в цепи.

 , то есть токи ветвей в момент резонанса равны.
, то есть токи ветвей в момент резонанса равны.
На практике

Построим векторную диаграмму токов.
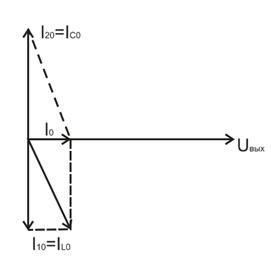 Общий ток по фазе совпадает по фазе с напряжением и он меньше токов ветвей цепи.
Общий ток по фазе совпадает по фазе с напряжением и он меньше токов ветвей цепи.
В идеальном колебательном контуре суммарный ток параллельных ветвей при резонансе равен нулю, то есть в контуре протекают токи I1 и I2 без учета генератора. Энергия от генератора конденсатора не тратится, и в контуре возникают незатухающие колебания.
 В реальном колебательном контуре имеется обмен энергией между электрическим полем конденсатора и магнитным полем катушки индуктивности в равных количествах. От генератора поступает столько энергии в контур, сколько тратится безвозвратно на его активных сопротивлениях.
В реальном колебательном контуре имеется обмен энергией между электрическим полем конденсатора и магнитным полем катушки индуктивности в равных количествах. От генератора поступает столько энергии в контур, сколько тратится безвозвратно на его активных сопротивлениях.
S=Pcosφ=Po=IoU
cosφ=1 Q=0.
График зависимости токов в реальном контуре:

Задача: Определить входное сопротивление для последовательного и параллельного колебательных контуров, если индуктивность составляет 400 мкГн, емкость 1600 пФ, сопротивление 30 Ом.
Решение:
Тема занятия 12: Избирательные свойства
параллельного колебательного контура.
12.1 Входные АЧХ и ФЧХ параллельного контура.
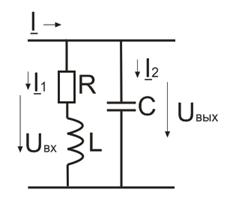


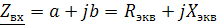



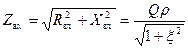 входная ФЧХ параллельного колебательного контура
входная ФЧХ параллельного колебательного контура
Построим график:



ξ=∞ Z=0
Вывод: параллельный колебательный контур имеет наибольшее сопротивление на резонансной частоте, по мере увеличения расстройки сопротивление уменьшается.
 φ=arctg(+X/R)=arctg(-ξ) - входная ФЧХ параллельного колебательного контура.
φ=arctg(+X/R)=arctg(-ξ) - входная ФЧХ параллельного колебательного контура.
Построим график:

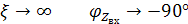
ξ→ -∞ φ → 90°
ξ = 1 φ = -45°
ξ = -1 φ = 45°
Вывод: ФЧХ параллельного колебательного контура представляет собой зеркальное отображение ФЧХ последовательного контура. На частотах меньших частоты собственных колебаний контур носит активно-индуктивный характер, на резонансной частоте – чисто активный, на частотах больших частоты собственных колебаний – активно –емкостной характер.
12.2 Подключение параллельного колебательного контура
к источникам тока и напряжения.
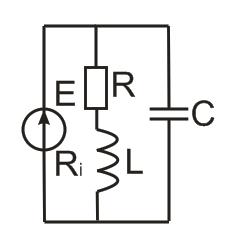
Для параллельного колебательного контура:
 - общий ток цепи при резонансе.
- общий ток цепи при резонансе.
 - ток в ветвях цепи.
- ток в ветвях цепи.
Найдем соотношение:


 , где Q – добротность контура, показывает, во сколько раз ток в разветвленной ветви больше тока в неразветвленной части цепи.
, где Q – добротность контура, показывает, во сколько раз ток в разветвленной ветви больше тока в неразветвленной части цепи.
В реальных устройствах выходное напряжение снимают с конденсатора. Если параллельный колебательный контур подключен к источнику напряжения с малым внутренним сопротивлением, то напряжение на входе равно напряжению на выходе и K=1, то есть колебательный контур не обладает избирательностью по напряжению. Ток в неразветвленной части цепи не остается постоянным.
Чтобы параллельный контур обладал избирательностью по напряжению , его необходимо подключить к источнику тока, то есть последовательно с ЭДС включить большое внутреннее сопротивление:
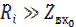 , тогда I=U/(Ri+Zвх)= сonst
, тогда I=U/(Ri+Zвх)= сonst

Схема с источником напряжения преобразуется в схему с источником тока.
Наличие резистора изменит добротность цепи.
Uвых=IUвх, следовательно так как I=const, то выходное напряжение изменяется по закону входного сопротивления контура, то есть контур обладает избирательностью
Построим графики зависимостей Uвых(f) и I(f) для обеих схем.
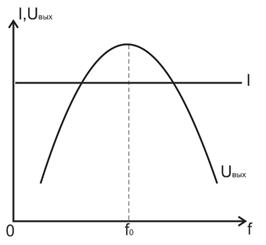
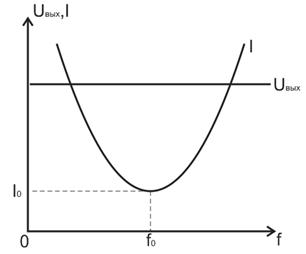
Для схемы с источником напряжения. Для схемы с источником тока.
Вывод: Колебательный контур обладает избирательностью по напряжению, если контур подключен к источнику тока.
Так как для схемы с источником тока при вводе сопротивления Ri изменяется добротность цепи, то используется понятие эквивалентной добротности.
Q=ρ/R Qэ=Q/(1+Zвх/Ri)
В реальных устройствах
 и
и  .
.
Эквивалентная обобщенная расстройка:
 .
.
12.3 Передаточные АЧХ параллельного колебательного контура.
Модуль передаточной функции:
K = Uвых / Uвх = IZвх/ Uвх = Qρ / Ri √1+ξэ² - передаточная АЧХ параллельного колебательного контура
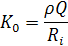 - коэффициент передачи при резонансе( ξэ=0) → max.
- коэффициент передачи при резонансе( ξэ=0) → max.
Найдем отношение
k/ko=1/√1+ξэ² -передаточные АЧХ параллельного колебательного контура в относительных единицах

Построим график:




- полоса пропускания абсолютное значение

- полоса пропускания относительное значение
Вывод: избирательность по напряжению получается , когда k<1, так как входное сопротивление значительно меньше внутреннего.
Задача: На рисунке дана схема. Найти емкость, добротность входное сопротивление, эквивалентную добротность, напряжение входа и ρ, если
 Fо=60Мгц
Fо=60Мгц
L=0,35 мкГн
R=5 Ом
E=10 мкВ
Ri=3 кОм.
Решение:
12.4. Виды параллельных колебательных контуров.
Контур первого вида :
 - условие для того, чтобы контур обладал избирательностью по напряжению и работал нормально.
- условие для того, чтобы контур обладал избирательностью по напряжению и работал нормально.
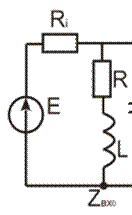 Ri – внутреннее сопротивление источника, величина определенная.
Ri – внутреннее сопротивление источника, величина определенная.
Zвх – входное сопротивление контура, тоже величина определенная.
На практике данное равенство может не соблюдаться, поэтому для его выполнения меняют  с помощью неполного включения контура, при котором часть индуктивности переносится из одной веви в другую, при этом
с помощью неполного включения контура, при котором часть индуктивности переносится из одной веви в другую, при этом  не изменяются.
не изменяются.
Ri изменять не можем, поэтому уменьшаем входное сопротивление контура. Это достигается с помощью автотрансформаторного или неполного включения контура, то есть включение, при котором часть емкостей или индуктивностей переносят из одной ветви в другую так, чтобы резонансная частота и добротность оставались неизменными.
Контур второго вида
 L=L1+L2
L=L1+L2
Поменяется коэффициент включения контура – это отношение индуктивности в первой ветви цепи к суммарной индуктивности контура.

При таком включении входное сопротивление контура уменьшается в P² раз.


Изменение схемы контура приводит к тому, что кроме резонанса токов на частоте:

появляется еще резонанс напряжений на частоте
 ,
,
так как есть участок с последовательным соединением индуктивности и емкости.
Контур третьего вида
 Аналогично катушкам разобьем емкости:
Аналогично катушкам разобьем емкости:
 коэффициент включения
коэффициент включения
Pc=С2/С1+С2=С2/С<1
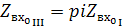

Вывод: Изменяя индуктивность или емкости между ветвями можно изменить входное сопротивление контура, не изменяя частоту или добротность.
Регулируя коэффициент включения контура можно получить равенство сопротивлений первого и второго контуров и внутреннего сопротивления источника, то есть получится согласованный режим работы цепи, при котором в цепь отдается максимальная мощность.
12.4 Сравнение последовательного и параллельного
колебательных контуров.
| последовательный | параллельный |
| 1. резонанс напряжений φ=0 Xl=Xc cosφ=1 | 1. резонанс токов φ=0 Bl=Bc cosφ=1 |
2. входная АЧХ
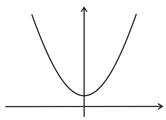 На резонансной частоте входное сопротивление контура минимально и равно активному.
На резонансной частоте входное сопротивление контура минимально и равно активному.
| 2. входная АЧХ
 На резонансной частоте входное сопротивление контура максимально и равно Qρ На резонансной частоте входное сопротивление контура максимально и равно Qρ
|
| 3. общий ток Io=U/Zвх=U/R- max | 3. общий ток Io=U/Zвх=U/Qρ- min |
| 4. добротность Q=Uвых/Uвх=Ul/U=k | 4. добротность Q=Il/I=Ic/I |
| 5 S=P Ql=Qc, Q=0 реактивная мощность | 5 S=P Ql=Qc, Q=0 реактивная мощность |
Тестовые задания:
Тема занятия 13: Электронные аналоги колебательных контуров.
Электронными аналогами колебательных контуров являются:
- электронный колебательный контур;
- гиратор;
- реактивный двухполюсник;
- прохождение через колебательный контур сигналов негармонической формы;
13.1 Гиратор
Гираторы - это активная цепь с двумя ИТУН на входе и выходе, токи которых пропорциональны напряжениям входа и выхода.
Гиратор позволяет имитировать индуктивность с помощью ARC- цепи.
В гираторах нет катушек, а следовательно их можно изготовить в виде микросхем. Входное сопротивление представленной схемы носит индуктивный характер.
Zвх=U1/Iвх=R²/Zн
Zн=1/jώс, следовательно
Zвх=R²jώс=jώR²C=jώLэкв
R1=R2=R3=R4=....=R
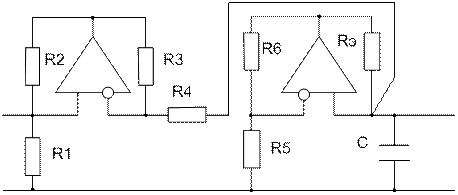
Например R=1 кОм, С=1 мкФ, тогда
Lэкв= СR²=1 Гн – подобные индуктивности в виде катушек имели бы весьма большие габариты.
Электронные индуктивности в виде микросхемы имеют малые габариты.
Эквивалентная индуктивность определяется сопротивлением и емкостью.
Тема занятия 14: Реактивные двухполюсники.
Реактивные двухполюсники – это цепи, имеющие два входных зажима и составляющие из индуктивностей и емкостей.
Двухполюсники, в которых число индуктивностей и емкостей равны или отличаются на единицу называются приведенными.
Так как реактивный двухполюсник представляет собой цепь без потерь, то:
- их входное сопротивление равно нулю при резонансе напряжений;
- и равно бесконечности при резонансе токов.
Частоты, при которых входное сопротивление равно нулю называются нулевыми частотами.
Частоты, при которых входное сопротивление равно бесконечности называют полюсными частотами.
В приведенных схемах резонансная частота на единицу меньше, чем элементов, а нулевые и полюсные частоты чередуются.

 В данной схеме: система из L2 и С – колебательный контур, резонанс в котором на полюсной частоте. Если частота не равна полюсной, то эта система может иметь либо индуктивный характер , либо емкостной. Входная ФЧХ параллельного колебательного контура.
В данной схеме: система из L2 и С – колебательный контур, резонанс в котором на полюсной частоте. Если частота не равна полюсной, то эта система может иметь либо индуктивный характер , либо емкостной. Входная ФЧХ параллельного колебательного контура.
Поэтому, если частота больше полюсной частоты, то АД – последовательный колебательный контур, в котором резонанс напряжений наступает на частоте большей полюсной.

 – последовательный колебательный контур, резонанс возникает на нулевой частоте.
– последовательный колебательный контур, резонанс возникает на нулевой частоте.
 Входная ФЧХ последовательного колебательного контура
Входная ФЧХ последовательного колебательного контура
Если частота больше нулевой, то система LC1 носит индуктивный характер, если полюсная частота больше нулевой, то LC1-C2 – параллельный колебательный контур.
Чтобы найти нулевую и полюсную частоты необходимо:
- записать входное сопротивление в виде дроби;
- нулевая частота находится если входное сопротивление равно нулю, то есть числитель приравниваем к нулю.
- полюсная частота находится если входное сопротивление равно бесконечности, то есть знаменатель приравниваем к нулю.


Нулевая частота: ώoL1-ώo³L1L2C+ώoL2=0
Нулевая частота не равна нулю, так как мы изучаем переменный ток и , следовательно ее можно сократить.
-ώo²L1L2C+L1+L2=0
Нулевая частота не может быть меньше нуля ώo=√(L1+L2)/L1L2C
Полюсная частота: 1-ώ∞²L2C , следовательно ώ∞=1∕√L2C
Если нулевая частота больше полюсной - оценить самостоятельно.
Правила построения Zвх=f(ώ):
1 Так как входное сопротивление может носить либо индуктивный, либо емкостной характер, то при ώ=∞, то входное сопротивление может быть равно нулю или -∞.
2 Сопротивление цепи из индуктивности и емкости носит только возрастающий характер, то есть изменится от 0 до ∞ или от -∞ до +∞.
3 Резонансных частот на единицу меньше элементов в цепи.
4 Нулевая и полюсная частоты чередуются.


14.1 Прохождение через колебательный контур сигналов негармонической формы.
Спектр периодической негармонической функции состоит из множества гармонических кратных частот.
Сигнал прямоугольной формы содержит частоты f1,f2,f3.....
Q=10 П = f0/Q = 0,1f0
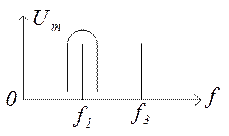
f0 = 1/2π√CL = f1
Полоса пропускания в 30 раз меньше частоты f3, входящей в спектр.
Таким образом практически через контур проходит сигнал только одной частоты.
Вывод: если ко входу колебательного контура приложить сигнал негармонической формы на выходе сигнал будет иметь гармоническую форму.
Если увеличивать сопротивление, то увеличится полоса пропускания, уменьшится добротность и появится явление «просачивания» напряжения с иными частотами, и кривая выходного напряжения станет искажаться.
Тестовые задания:
Тема занятия 17: Связанные колебательные контуры.
Виды связи.
Два контура являются связанными, если изменение тока в одном из них вызывает изменение напряжения или тока в другом. То есть ЭДС одного контура переходит в другой, в результате контура обмениваются энергией.
Элемент, общий для обоих контуров называется сопротивлением связи. В зависимости от него различают следующие виды связи:
1.индуктивную(трансформаторную или автотрансформаторную);
2.внутреннюю емкостную;
3.внешнюю емкостную.
Трансформаторная связь осуществляется через взаимоиндуктивность.
 М-коэффициент взаимной индукции
М-коэффициент взаимной индукции
Действие основано на явлении взаимной индукции, то есть под действием тока в первичной катушке возникает магнитный поток, который пронизывает вторичную катушку, наводит в ней ЭДС взаимоиндукции. От нее возникает ток I .
Z=jώΜ.
Автотрансформаторная. От тока в первичном контуре создается падение напряжения на L , следовательно и от него потечет ток I .



Внутренняя емкостная.


Под действием тока создается падение напряжение на связывающей емкости, от которого начнет протекать ток  .
.
Взаимное влияние контуров друг на друга определяется коэффициентом связи, который изменяется от нуля до единицы.
 ,
,
где - реактивное сопротивление связи, то есть мнимая часть связанного сопротивления.
- сопротивления первого и второго контуров, имеющих тот же характер, что и сопротивление связи.
Рассчитаем коэффициент связи для каждого включения:
1. Трансформаторное.
X=ώM
X1ֽ=ώL1ֽ
X2=ώL2
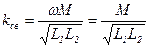
2. Автотрансформаторное.

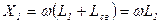
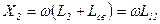
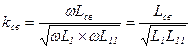
3. Внутренняя емкостная.


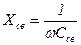


17.2 Одноконтурная схема замещения связанных контуров
Через Z1 обозначены элементы, входящие только в первый контур, через Z2 – только во второй.
Zсв – сопротивление связи.
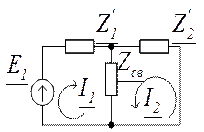


Составим уравнение по методу контурных токов:


Обозначим:


полные сопротивления 1-го и 2-го контура
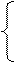

Выразим все сопротивления:

На практике Хсв << Х1 и Х2 и им можно пренебречь


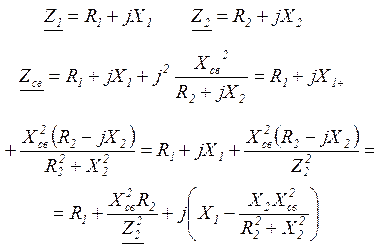
Rвх Хвх
Вторые слагаемые называются вносимыми:
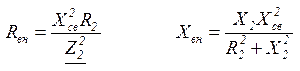
Тогда: 
Мы можем исходную двухконтурную схему заменить эквивалентной одноконтурной, в которой все элементы первичного контура остаются без изменений, а вместо элементов вторичного контура в первичный включаются вносимые сопротивления.
Вносимые сопротивления обусловлены влиянием вторичного контура на процессы, происходящие в первичном.
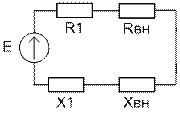
Вносимые сопротивления обладают тем свойством, что в них рассеиваются такие же активные и реактивные мощности, которые рассеиваются в элементах вторичного контура.
17.2 Физический смысл вносимых сопротивлений.
Настроим оба контура в резонанс: X1=X2=0.
Векторная диаграмма в момент резонанса:


E1 и I1 совпадают по фазе, так как в первичном контуре резонанс.
Под действием тока I1 возникает магнитный поток, который вызывает взаимоиндукцию. Эта ЭДС отстает от тока на 90°. Ток I2 совпадает с Е2 по фазе, так как и второй контур настроен в резонанс. Вокруг второй обмотки от тока I2 возникает свой магнитный поток, который будет пронизывать первую обмотку и наводить в ней ЭДС взаимоиндукции . Эта ЭДС отстает от тока I2 на 90° и противоположна ЭДС самоиндукции Е1, следовательно

То есть из-за наличия E’1 ток I1 уменьшается.
При расчетах уменьшение I1 учитывается с помощью вносимого сопротивления.
I1=E1∕(R1+Rвн)=Е1/Rвх, так как для одиночного контура I1=E1/R1.
Физический смысл вносимого сопротивления.
Вносимое сопротивление отражает уменьшение тока первого контура из-за влияния тока второго контура, то есть отражает возникновение противо- ЭДС.
Физический смысл вносимого реактивного сопротивления:
Из-за влияния второго контура на первый изменяется резонансная частота. Это изменение учитывается реактивным сопротивлением. Знак «-» в (X1 - Xвн) означает, что если реактивное сопротивление второго контура носит индуктивный характер, то в первичный добавляется как бы емкостное сопротивление наоборот.
Тема занятия 18: Резонансы в связанных колебательных контурах.
Настроить связанные контура – это значит получить максимальный ток во втором контуре. Этого можно добиться с помощью подборки емкостей или сопротивления связи.

В результате настройки можно получить:
1) первый частный резонанс получится изменением С1(в резонанс настроится первый контур);
2) второй частный резонанс получается изменением С2 (в резонанс настраивается второй контур);
3) полный резонанс. Оба контура настроены в резонанс, а затем добиваются максимального тока подбором сопротивления связи;
4) сложный резонанс. Это сочетание одного из частных резонансов с подбором сопротивления связи.
18.1 Первый частный резонанс.
Е и f остаются постоянными.
Изменяя С1, добиваемся резонанса в первом контуре.
 - резонансная частота.
- резонансная частота.
X1=ώL1-1∕ώC1 – реактивное сопротивление изменяется, так как изменяется С1.
Xвх = X1+Xвн – тоже изменяется.
При резонансе ток во входной цепи совпадает по фазе с входным напряжением. Это возможно, если сопротивление первого контура – активное.
Xвх=Х1+Хвн=0
Х1=-Хвн - условие первого частного резонанса.
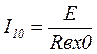 , то есть ток увеличивается.
, то есть ток увеличивается.
Так как I1 максимален , то он вызывает максимальный магнитный поток. Этот поток пронизывает вторичную обмотку, вызывая Е2 – максимальное, следовательно во вторичном контуре будет протекать I2- максимальный.
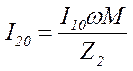
В этом случае во втором контуре течет максимальный ток, но не наибольший из возможных токов.
18.2 Второй частный резонанс.
Источник переносят временно во второй контур, и изменяя С2 настраивают в резонанс на частоте:
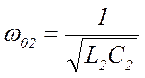
При этом из первичного контура во вторичный вносится сопротивление
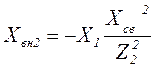
Тогда общее реактивное сопротивление второго контура
Хвх2= Х2+Хвн2 =0
Х2=-Хвн2 условие второго частного резонанса
При этом сопротивление контура – число активное и минимальное, а следовательно I2 – максимален.
Ток I2 на резонансной частоте максимален, но не наибольший из возможных.
18.3 Полный резонанс.
Порядок настройки:
1) устанавливаем самую слабую связь между контурами, то есть М – минимально и настроим первые контур в резонанс.
Х1=0 ώ=ώ0
2) настраиваем второй контур в резонанс.
Х2=0 ώ=ώ0
 Xвх=Х1+Хвн=0
Xвх=Х1+Хвн=0
Х1=Х2=Хвн=0 - условие полного резонанса
Схема замещения контуров при полном резонансе:


3) усиливаем связь между контурами до тех пор, пока во вторичном контуре не потечет максимальный ток.
I2mm (максимум - максиморум)
Связь, при которой потечет такой ток называется критический.
kсв=kкр
Критическая связь численно равна затуханию каждого контура.
Коэффициент взаимной индукции при которой получается критическая связь:

При критической связи:

Х1=Х2=Хвн=Хвх=0
Rвн0=R1 условие полного резонанса
18.4 Сложный резонанс
Получается при сильной связи, при этом
Хвх=Х1+Хвн=0
Ток I2mm возникает не на резонансной частоте, а на двух других частотах, близких к ней. Эти частоты называются частотами связи и на них работают радиопередающие устройства.
18.5 Передаточные АЧХ связанных контуров.
Полоса пропускания.
Фактор связи характеризует влияние одного контура на другой
ηсв=kсв/kкр

Передаточная АЧХ связанных контуров зависит не только от добротности, но и от степени связи между контурами.
Тестовые задания:
| Какую избирательность обеспечивает связанная система при расстройке на Δf=50 кГц, если L=L1=L2=1 мГн, С=С1=С2=1нФ, R=R1=R2=20 Ом. | |
| Что называется коэффициен-том связи. Для какого типа включения kсв=ώM/√ώ²L1L2. | А) трансформаторное; Б) автотрансформаторное; В) внутреннее емкостное. |
| Укажите условие для получения полного резонанса | 1) Х1=-Хвн 2) Х2=-Хвн2 3) Х1=Х2=Хвн=0 4) Хвх=Х1+Хвн=0 |
Тема занятия 19: Переходные процессы в линейных электрических цепях.
До этих пор рассматривались цепи, в которых:
1. Источники были подключены к цепи теоретически бесконечно равны;
2 Никаких изменений в состоянии цепи не производилось.
Режимы работы, имеющиеся при этих условиях, называются установившимися (вынужденными или принужденными).
Однако, всякому установившемуся режиму работы предшествует переходной процесс, при котором в цепи в течение весьма короткого промежутка времени изменяются ток, падение напряжения на участках, электрические заряды конденсаторов и энергия электрических и магнитных полей.
Переходным процессом называется особое явление, возникающее в электрической цепи при включении и отключении источников электрической энергии, питающих электрические цепи, или при изменении величины параметров цепи R,L,M,C.
По окончании переходного процесса в цепи снова наступает установившийся режим.
Временем переходного процесса называют промежуток времени между началом и концом переходного процесса, являющимся началом установившегося режима.
Под коммутацией понимают подключение, отключение, переключение источников или каких-либо элементов цепи.
При анализе переходного процесса в электрических цепях для определения начальных условий пользуются двумя законами коммутации.
19.1 Законы коммутации.
1. Ток в катушке индуктивности не может измениться скачком. В начальный момент после коммутации ток в цепи с индуктивностью остается таким же, каким он был непосредственно перед коммутацией, а затем плавно изменяется в течение времени коммутации Δt.
i-(0)=i+(0)
до коммутации после коммутации
2. В начальный момент после коммутации напряжение на емкости остается таким же, как оно было непосредственно перед коммутацией, а затем плавно изменяется в течение времени коммутации Δt.
Uc-(0)=Uc+(0)
Под моментом t=-0 понимают последний момент времени перед коммутацией, а под моментом t=+0 первый момент времени после коммутации. В момент t=-0 все напряжения и токи находятся в состоянии установившихся значений для той цепи, которая имелась до коммутации. В момент времени t=+0 в цепи начинается переходной процесс.
Таким образом свойства цепей в последний момент перед коммутацией и в первый момент после коммутации оказывается совершенно различными, могут быть противоположными.
Доказательства:
1. U=Ldi∕dt Если предположить, что ток изменяется мгновенно, то есть di∕dt→∞, то U→∞ и ρ→∞ , где
ρ=dW/dt - мощность стремится к бесконечности, что не имеет физического смысла, то есть не существует источников электрической энергии бесконечных величин мощностей.
2. i=CdU/dt ,если предположить, что напряжение изменится скачком, то есть dU/dt →∞, то ток и мощность стремятся к бесконечности, что также не имеет физического смысла.
В цепях с одним накопителем энергии процессы описываются дифференциальными уравнениями первой степени (первого порядка), следовательно RL и RC цепи называют цепями первого порядка.
Цепи второго порядка – это цепи, процессы в которых описываются дифференциальными уравнениями второго порядка. Это цепи RLC и любые цепи, имеющие два накопителя энергии.
19.2 Расчет переходных процессов.
Переходные процессы рассчитываются с использованием двух составляющих:
- принужденной (вынужденной);
-свободной (две составляющие появляются в результате решения дифференциальных уравнений общего и частного решения).
Принужденная показывает ток или напряжение, которые будут через бесконечно большое время, то есть когда переходной процесс закончится. Эта составляющая рассчитывается обычными методами.
Для нахождения свободной составляющей необходимо составить дифференциальное уравнение цепи с использованием второго закона Кирхгоффа и приравнять его к нулю.
Тема занятия 19: Переходные процессы в RL-цепи.
19.1 Анализ переходных процессов при включении RL цепи
на постоянное напряжение.
 Пусть ключ находится в положении 1. До коммутации , то есть в интервале от t=
Пусть ключ находится в положении 1. До коммутации , то есть в интервале от t= до t=-0 ключ был разомкнут, источник отключен, ток в цепи равен нулю и напряжение на всех элементах равно нулю.
до t=-0 ключ был разомкнут, источник отключен, ток в цепи равен нулю и напряжение на всех элементах равно нулю.
Уравнения для определения тока в переходном режиме следует составлять для состояния цепи после коммутации.
Ключ в положении 1:
По второму закону Кирхгоффа: Uвх =UR+U1
Выразим: UR=Ri Uвх=U, следовательно UL=L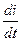
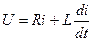
 - дифференциальное уравнение первого порядка с правой частью.
- дифференциальное уравнение первого порядка с правой частью.
Решением такого уравнения будет сумма двух решений - общего и частного.
В электронике i=iвын+iсв
Чтобы определить вынужденную составляющую искомой переменной величины, следует все производные положить равными нулю и решить получившиеся уравнения (использовать определение принужденной составляющей).
Если  , то по окончании переходного процесса в цепи установится ток
, то по окончании переходного процесса в цепи установится ток  , так как XL при постоянном токе равно нулю, а сопротивление всей цепи равно R.
, так как XL при постоянном токе равно нулю, а сопротивление всей цепи равно R.
Свободной называется составляющая тока изменяющаяся по такому закону, который обуславливается свойствами самой системы, а не какими-либо внешними воздействиями или причинами.
Чтобы определить законы свободной составляющей, следует в уравнении исключить внешнее воздействие, то есть положить U=0 и решить получившееся уравнение.

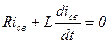
Решением данного уравнения будет  , где А – постоянная интегрирования;
, где А – постоянная интегрирования;
р – корень характеристического уравнения цепи;
Чтобы его найти произведем замену:
iсв на 1.

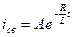
Величина  - постоянная времени цепи RL.
- постоянная времени цепи RL.
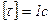
 ,
, 
Чтобы найти А, воспользуемся первым законом коммутации:
i-(0)=i+(0).
Запишем значения тока в первый момент времени после коммутации:
i+(0)=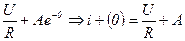
Значение тока в последний момент перед коммутацией:
i-(0)=0, так как ключ был разомкнут и в цепи ток не протекал.
Так как i-(0)=i+(0), то 
Значит: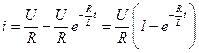 , следовательно
, следовательно
 - уравнение тока при включении RL цепи на постоянное напряжение.
- уравнение тока при включении RL цепи на постоянное напряжение.
 Постоянной времени цепи
Постоянной времени цепи  называется время, за которое свободная составляющая тока или напряжения уменьшается в е раз, или это время, за которое ток достигает значения 0,63 от установившегося.
называется время, за которое свободная составляющая тока или напряжения уменьшается в е раз, или это время, за которое ток достигает значения 0,63 от установившегося.
Если 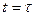 , то
, то 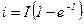 =0,63I
=0,63I
Можно рассчитать, что ток достигает 99% установившегося значения через время равное 4,6 , то есть tпер.пр.=4,6
, то есть tпер.пр.=4,6 .
.
19.2 Отключение RL цепи от источника постоянного напряжения.
Пусть ключ находится в положении 2.
 В данном случае ток устанавливающегося режима в катушке, не поддерживаемый ЭДС источника электрической энергии, начинает уменьшаться. При этом уменьшается магнитный поток катушки и в катушке индуцируется ЭДС самоиндукции, которая имеет одно направление с током, следовательно, ток уменьшается не мгновенно, а за некоторое время переходного процесса.
В данном случае ток устанавливающегося режима в катушке, не поддерживаемый ЭДС источника электрической энергии, начинает уменьшаться. При этом уменьшается магнитный поток катушки и в катушке индуцируется ЭДС самоиндукции, которая имеет одно направление с током, следовательно, ток уменьшается не мгновенно, а за некоторое время переходного процесса.

Ток переходного процесса равен нулю , так как через бесконечно большое время, тока в цепи не будет.
Для нахождения 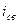 , составляем уравнение по второму закону Кирхгоффа и приравниваем входное уравнение к нулю, так как его и нет в цепи.
, составляем уравнение по второму закону Кирхгоффа и приравниваем входное уравнение к нулю, так как его и нет в цепи.






 , где
, где  - постоянная времени.
- постоянная времени.
Решение дифференциального уравнения :  .
.
Найдем параметр А, используя первый закон коммутации.


Найдем значение тока в первый момент после коммутации:
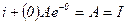 - используя первый закон коммутации.
- используя первый закон коммутации.

Тогда уравнение тока при отношении цепи:

Если t= , то
, то  определение
определение  смотри выше.
смотри выше.
Чем больше  ,тем медленнее идет переходной процесс.
,тем медленнее идет переходной процесс.
Постоянная времени определяется параметрами всех элементов, входящих в цепь.
Построим зависимость i(t).


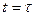

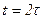
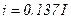

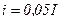
 4
4




Задачи:
1. Рассчитать  , если сопротивление 10 Ом, индуктивность 1 Гн (отключ. от постоянного источника напряжения), ток 10 А, iτ=3,7А.
, если сопротивление 10 Ом, индуктивность 1 Гн (отключ. от постоянного источника напряжения), ток 10 А, iτ=3,7А.
2. Рассчитать  и найти сопротивление R, если напряжение U=50 В, индуктивность L=6 Гн (включ.), t=0,25 c, i=0,9I
и найти сопротивление R, если напряжение U=50 В, индуктивность L=6 Гн (включ.), t=0,25 c, i=0,9I
Тема занятия 20: Переходные процессы в RC цепи.
20.1 Заряд конденсатора.
При замыкании ключа конденсатор заряжается до напряжения источника, в цепи возникает переходной процесс.
U=UR+Uc=RI+UC – второй закон Кирхгоффа. При последовательном соединении элементов напряжение на зажимах равно сумме напряжений на участках цепи.
i=CdUc/dt;
U=RCdUc/dt+UC – дифференциальное уравнение.
Его решение UC=UCприн+UСсв
τ =RC
При t=∞ переходные процессы заканчиваются , напряжение на конденсаторе не изменится и становится постоянным dUc/dt=0, следовательно из выражения
U=RCdUc/dt+UC получаем Uс вын=U.
По окончании переходного процесса постоянный ток перестает протекать через емкость, падение напряжения на сопротивлении становится равным нулю и напряжение на конденсаторе оказывается равным напряжению источника.
Определим свободную составляющую напряжения на конденсаторе. Приравняем дифференциальное уравнение к нулю:
RCdUc/dt+UC=0
P+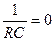 - характеристическое уравнение, следовательно
- характеристическое уравнение, следовательно
 .
.
Решение уравнение:
Uс св=Аe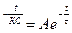 , то есть Uc=U+Ae
, то есть Uc=U+Ae
Найдем параметр А. Воспользуемся вторым законом коммутации.
Uc-(0)=Uc+(0)
Uc-(0)=0, так как цепь была разомкнута.
В первый момент после коммутации:
Uc+(0)=Uc прин(0)+Uссв(0)=U+Ae0=U+A=0
A=-U
Uссв=-Ue
Тогда : закон изменения напряжения на конденсаторе при его заряде будет иметь вид
Uc=Ucприн+Uссв=U-Ue =U(1-e
=U(1-e )
)
Так как ток зарядки 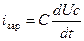 , то
, то
 - закон изменения зарядного тока.
- закон изменения зарядного тока.

Uc=f(t)- построим эту зависимость:
t=0 Uc=0
t= Uc=0,63U
Uc=0,63U
t=2 Uc=0,86U
Uc=0,86U
t=3 Uc=0,95U
Uc=0,95U
t=4 Uc=0,98U
Uc=0,98U
t=4,6 Uc=0,99U
Uc=0,99U
Физический смысл  при заряде конденсатора – это время, за которое напряжение на конденсаторе достигает значения 0,63 от установившегося значения U.
при заряде конденсатора – это время, за которое напряжение на конденсаторе достигает значения 0,63 от установившегося значения U.
20.2 Разряд конденсатора

Ключ находится в положении 2, то есть уже имеется конденсатор, заряженный до значения напряжения.
Ток в цепи 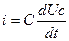 .
.
Составляем уравнение по второму закону Кирхгоффа, так как источников в цепи нет, то
0=UC+UR
RC решением уравнения будет
решением уравнения будет
Uc=Ucприн+Uccв
Так как через t=∞ конденсатор полностью разряжается, Uсприн=0.
Определим Uссв:
0=RC
Uссв= А =
= , где τ=RC, из математики Uссв
, где τ=RC, из математики Uссв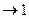 и
и 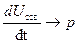 , на основании этого производим замену и получаем:
, на основании этого производим замену и получаем:
0=RCp+1, следовательно p=-
Uссв=
Находим параметр А, используя второй закон коммутации
Uc-(0)=Uc+(0)
Uc-(0)=U
Находим значение напряжения в первый момент после коммутации:
Uc+(0)=Uс пр(0)+Uс св(0)=0+Аe0=U
A=U
Следовательно:
Uс св=Ue
Тогда закон изменения напряжения на конденсаторе при его разряде:
Uc=Uc пр+Uс св=0+ Ue = Ue
= Ue
Iразр=С
iразр= -Ie - закон изменения разрядного тока
- закон изменения разрядного тока
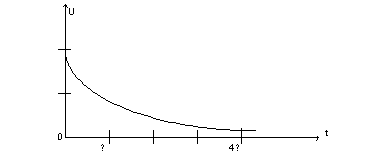 Построим зависимости Uc(t):
Построим зависимости Uc(t):
t=0 Uc=U
t= Uc=0,37U
Uc=0,37U
t=2 Uc=0,137U
Uc=0,137U
t=3 Uc=0,05U
Uc=0,05U
t=4 Uc=0,018U
Uc=0,018U
t=4,6 Uc=0,01U
Uc=0,01U
Через время переходного процесса 4,6τ напряжение на конденсаторе будет близко к нулю.
Физический смысл τ при разряде конденсатора – это время, за которое напряжение на конденсаторе уменьшится в 2,7 раза(или e) по сравнению с первоначальным.
 Задача 1: Напряжение на зажимах цепи 300 В, емкость конденсатора 100 мкФ, сопротивления 20, 80, 50 Ом соответственно, определить Uc(t) для цепи представленной на рисунке.
Задача 1: Напряжение на зажимах цепи 300 В, емкость конденсатора 100 мкФ, сопротивления 20, 80, 50 Ом соответственно, определить Uc(t) для цепи представленной на рисунке.
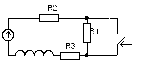 Задача 2: Е=75 В, сопротивления соответственно 75, 15 и 10 Ом, L=10 мГн. Найти i(t) для данной схемы.
Задача 2: Е=75 В, сопротивления соответственно 75, 15 и 10 Ом, L=10 мГн. Найти i(t) для данной схемы.
Тема занятия 21: Переходные процессы в цепях второго порядка.
Цепи второго порядка – это цепи, свободные процессы, в которых описываются дифференциальные уравнения второго порядка.
 Цепями второго порядка являются цепи с двумя накопителями энергии.
Цепями второго порядка являются цепи с двумя накопителями энергии.
Пусть до коммутации конденсатор был заряжен до напряжения U0.
Запишем второй закон Кирхгоффа после коммутации:
UC+UL+UR=0
UR=Ri UL=L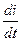 UC+Ri+L
UC+Ri+L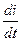 =0
=0
 - подставляем в уравнение
- подставляем в уравнение
UC+LC RC
RC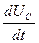 =0 разделим на величину LC,
=0 разделим на величину LC,

UC ПР=0, то есть конденсатор в замкнутом контуре полностью разряжается.
UC=UC CВ
Определим ее:
Составим характеристическое уравнение:
k2+Rk/L+1/LC=0 – решением уравнения будет
UC=A1e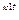 +A2e
+A2e , где k1 и k2 – корни характеристического уравнения
, где k1 и k2 – корни характеристического уравнения
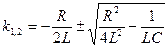
При этом может оказаться три случая:
1) R<2ρ – цепь с малым затуханием
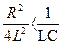
2) R>2ρ – цепь с большим затуханием

3) R=2ρ

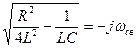
Обозначим 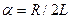 , получим:
, получим:

Если 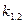 подставить в выражение UC=A1e
подставить в выражение UC=A1e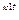 +A2e
+A2e и учесть два закона коммутации, то
и учесть два закона коммутации, то

 - начальная фаза свободных колебаний
- начальная фаза свободных колебаний

Построим график зависимости свободных затуханий от времени переходного процесса:
 Затухающая синусоида
Затухающая синусоида
Количество колебаний, совершаемых свободной составляющей за время переходных процессов равное Q.
21.1 Единичная функция
Единичной функцией называется скачкообразное изменение напряжения от 0 до 1.
Обозначают σ ( ) или 1(t).
) или 1(t).
Физически подключение цепи к источнику постоянного напряжения 1В есть воздействие в виде единичной функции.
σ(t)=1 – во временном виде
σ(p)=1/p – в оперативном виде.
21.2 Импульсная функция
δ(t) (дельта-функция) – есть производная от единичной функции, т.е. δ(t)=

В операторном виде 
Разберем форму дельта-функции. До момента, когда  единичная функция равна нулю
единичная функция равна нулю
σ(t)=0, тогда  =0 то есть δ(t)=0.
=0 то есть δ(t)=0.
В момент, когда  единичная функция скачком изменит свое значение, при этом угол увеличится до 900,
единичная функция скачком изменит свое значение, при этом угол увеличится до 900,  , где
, где  - угол наклона функции.
- угол наклона функции.
Дельта-функция стремится к бесконечности, но через бесконечно малое время  =0, следовательно через
=0, следовательно через  δ(t)
δ(t)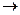 0. Площадь дельта-функции равна единице.
0. Площадь дельта-функции равна единице.
Таким образом импульсной функцией называется сигнал с бесконечно большой амплитудой, бесконечно малой длительностью, и площадью равна единице.
21.3 Переходная и импульсная характеристика цепей
Переходной характеристикой цепи по напряжению  называется закон, по которому изменяется выходное напряжение цепи при единичной функции на входе.
называется закон, по которому изменяется выходное напряжение цепи при единичной функции на входе.
Чтобы определить  , необходимо любым образом рассчитать выходное напряжение при подключении цепи к постоянному напряжению, а затем положить это напряжение равным единице.
, необходимо любым образом рассчитать выходное напряжение при подключении цепи к постоянному напряжению, а затем положить это напряжение равным единице.
 Определить
Определить  -?
-?
При подключении к источнику постоянного напряжения  , если напряжение равно единице, то переходная характеристика
, если напряжение равно единице, то переходная характеристика  .Операторная переходная характеристика
.Операторная переходная характеристика 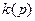 рассчитывается аналогично комплексной передаточной функции.
рассчитывается аналогично комплексной передаточной функции.


| <== предыдущая страница | | | следующая страница ==> |
| Весенний семестр. Одним из основных требований, предъявляемых к установочным элементам, является износостойкость, которая во многом обеспечивает условие долговечности | | | Весенний семестр |
Дата добавления: 2014-02-27; просмотров: 2517; Нарушение авторских прав

Мы поможем в написании ваших работ!