Энергия электростатического поля заряженных проводников в вакууме

Энергия W_e электрического поля в объеме V равна (в СГСЕ)

W_e =

V

Здесь интеграл по всему объему V пространства вне проводников, т. к. внутри проводника Е= 0. Используем связь E = – grad φ и тогда

W_e =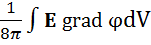

V

Используем известное выражение из векторной алгебры для произведения трех векторов a(bc) = c(ab) – b(ac) и тогда получим

W_e = – +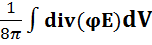

V V

Полагаем, что в пространстве между заряженными проводниками (вне проводников) зарядов нет, следовательно, div Е = 0 и второй интеграл = 0.

Первый интеграл по объему согласно теореме Остроградского-Гаусса преобразуется в интеграл по поверхностям на проводниках и на бесконечно удаленной от проводников поверхности. Но на последней Е= 0 и потенциал φ на бесконечности принимаем равным нулю, φ_∞ = 0.

Тогда, полагая потенциал на каждой поверхности n-ого проводника равным (или просто потенциал проводника) φ_a (a – 1……N – индекс n-ного проводника), а его заряд равным q_а можно записать для W_e:

W_e = ,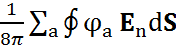

S_a

Здесь интеграл по замкнутой поверхности проводника с индексом «а» S_a.

Так как φ_а = const на поверхности проводника, следовательно, его можно вынести за знак интеграла, а 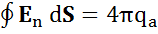и тогда

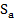
W_e =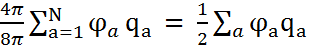

Можно ввести емкость по аналогии

q_a = ,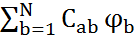

где C_aa – (при b = a) коэффициенты емкости, а C_ab – (при b ≠ a) коэффициенты электростатической индукции.

Если ввести обратное выражение для потенциала через заряд, то

φ_a = ,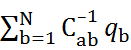

где коэффициенты 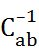составляют обратную матрицу матрице C_ab .

Коэффициенты C_ab = C_ba , 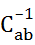= , C_aa > 0 и 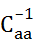> 0 , а при a ≠ b C_ab и 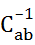< 0 .

Если меем только два проводника (обычный конденсатор), то полагая потенциал одного проводника равным нулю, например φ₁ = 0 , а разность потенциалов φ₁ – φ₂ = U = φ₂ , получим для W_e

W_e = 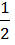C₂₂U². Известное вам выражение для энергии конденсатора имеет вид W_e = 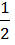CU² . Видно, что C₂₂ = C.

Дата добавления: 2014-02-28; просмотров: 408; Нарушение авторских прав

Мы поможем в написании ваших работ!