
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Примеры вычисления моментов инерции
 1) Момент инерции тонкого кольца (прямого тонкостенного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной плоскости кольца, проходящей через центр кольца:
1) Момент инерции тонкого кольца (прямого тонкостенного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной плоскости кольца, проходящей через центр кольца:
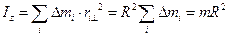 .
.
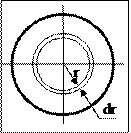 2) Момент инерции диска (сплошного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной к плоскости диска и проходящей через центр диска (сплошного цилиндра).
2) Момент инерции диска (сплошного цилиндра) массы m и радиуса R относительно оси z, перпендикулярной к плоскости диска и проходящей через центр диска (сплошного цилиндра).
Выделим тонкий цилиндр радиусом r и толщиной dr.
Масса этого цилиндра 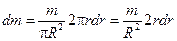 ,
, 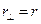 .
.
Поэтому 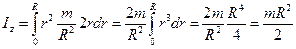 .
.
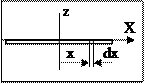 3) Момент инерции тонкого стержня относительно оси z, являющейся срединным перпендикуляром. Масса стержня m, длина L.
3) Момент инерции тонкого стержня относительно оси z, являющейся срединным перпендикуляром. Масса стержня m, длина L.
Выделим на расстоянии x от оси маленькую часть стержня длиной dx.
Масса этой части 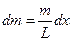 и
и 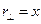 . Поэтому
. Поэтому
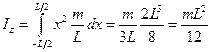 .
.
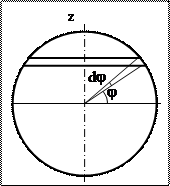 4) Момент инерции тонкостенного шара относительно любой оси симметрии z. Масса шара m, радиус R.
4) Момент инерции тонкостенного шара относительно любой оси симметрии z. Масса шара m, радиус R.
Выделим на поверхности сферы кольцевой сегмент, для которого ось z является осью симметрии. Сегмент опирается на малый центральный угол dj, положение сегмента определяется углом j, отсчитываемым от плоскости экватора, перпендикулярной оси z.
Тогда радиус кольца 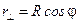 ,
,
его масса 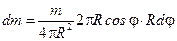 , поэтому
, поэтому
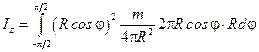 или
или
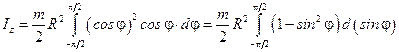 ,
,
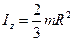 .
.
5) Момент инерции сплошного шара относительно любой оси симметрии z. Масса шара m, радиус шара R.
Представим шар как набор вложенных друг в друга тонкостенных сфер переменного радиуса r и толщиной dr. Масса одной такой сферы 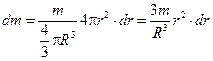 .
.
Момент инерции такой сферы 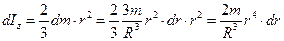 . Поэтому
. Поэтому
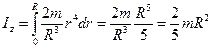 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Твердого тела вокруг неподвижной оси | | | Теорема Гюйгенса-Штейнера |
Дата добавления: 2014-03-04; просмотров: 760; Нарушение авторских прав

Мы поможем в написании ваших работ!