
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Теорема Гюйгенса-Штейнера
Как связаны между собой моменты инерции твердого тела относительно двух параллельных осей?
Рассмотрим две параллельные оси z1 и z2. Введём две системы координат так, чтобы их оси х и у были параллельны друг другу, причем вторая система координат была получена параллельным переносом из первой на вектор 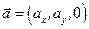 , перпендикулярный осям z1 и z2 . Тогда расстояние между осями будет равно
, перпендикулярный осям z1 и z2 . Тогда расстояние между осями будет равно 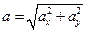 .
.
В этом случае координаты любой i-й малой частицы тела связаны соотношениями : 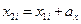 ,
, 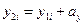 ,
, 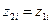 .
.
 Квадрат расстояния от этой частицы до первой оси z1:
Квадрат расстояния от этой частицы до первой оси z1: 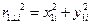
и до второй оси z2 : 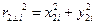 .
.
Вычисляем момент инерции относительно второй оси:
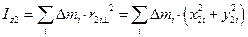 ,
,
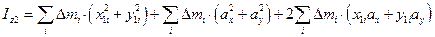 .
.
В этом равенстве
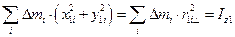 - момент инерции тела относительно оси z1,
- момент инерции тела относительно оси z1,
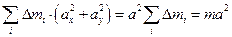 ,
,
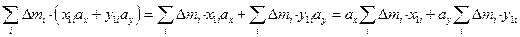 .
.
Учтём, что 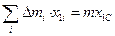 и
и 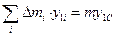 (где x1С и y1С – координаты центра масс тела в 1й системе координат), и получим:
(где x1С и y1С – координаты центра масс тела в 1й системе координат), и получим:
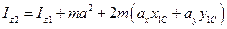 .
.
Если предположить, что ось z1 проходит через центр масс тела, то x1С =0 и y1С =0, поэтому в этом случае выражение упрощается:
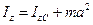 .
.
Это выражение носит название теоремы Гюйгенса-Штейнера: момент инерции твердого тела относительно произвольной оси равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс тела и квадрата расстояния между осями, умноженного на массу тела.
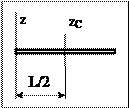 Пример. Момент инерции стрежня относительно оси, проходящей через край стержня, перпендикулярно ему, равен сумме момента инерции относительно срединной оси и массе, умноженный на квадрат половины длины стержня:
Пример. Момент инерции стрежня относительно оси, проходящей через край стержня, перпендикулярно ему, равен сумме момента инерции относительно срединной оси и массе, умноженный на квадрат половины длины стержня:
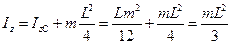 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Примеры вычисления моментов инерции | | | Закон сохранения момента импульса |
Дата добавления: 2014-03-04; просмотров: 548; Нарушение авторских прав

Мы поможем в написании ваших работ!