Лекция 3. Работа в электрическом поле. Потенциал электрического поля. Разность потенциалов

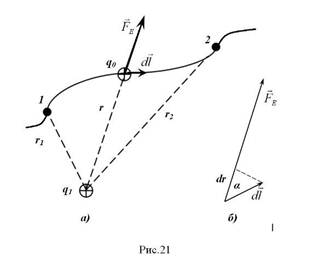1. Работа в электрическом поле. Рассмотрим движение точечного тела с электрическим зарядом q₀ из точки 1 в точку 2 в электрическом поле неподвижного (закрепленного) точечного тела с электрическим зарядом q₁ (рис.21). Для вычисления работы силы 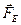при перемещении точечного тела с электрическим зарядом q₀ из т.1 в т.2 напишем формулу для работы силы 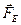при малом перемещении точечного тела с электрическим зарядом q₀:

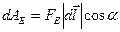(3.1). На рис.21,б малое перемещение 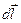и сила 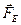изображены в увеличенном виде. Перемещение 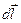должно быть малым настолько, чтобы при таком перемещении силу 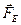можно было считать практически постоянной. Подставим в (3.1) формулу (1.5) и : 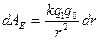(3.2). Знак модуля у электрических зарядов опущен, так как в нашем примере они положительные. Вычислим теперь работу силы 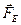на пути 1 → 2:

.

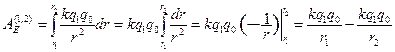Из формулы 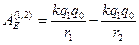(3.3) следует, что работа 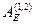не зависит от способа перехода точечного тела с электрическим зарядом q₀ из т.1 в т.2 и определяется расстояниями r₁ и r₂ от точек 1 и 2 до точечного тела с электрическим зарядом q₁ и электрическими зарядами q₁ и q₀. Это значит, что электрическое поле вокруг неподвижного точечного тела с электрическим зарядом q₁ является потенциальным, сила 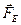– консервативной, а у точечного тела с электрическим зарядом q₀, находящегося в электростатическом поле, есть потенциальная энергия W_E.

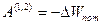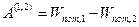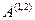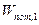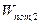В потенциальном поле или (3.4). В этом равенстве – работа консервативной силы, и – потенциальная энергия тела (системы) в первом и втором состояниях. В нашем примере 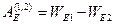(3.5). Из сопоставления (3.3) и (3.5) следует, что в данном случае 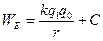(3.6), где С – постоянная. Потенциальную энергию 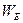принято считать равной нулю при 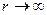. При таком выборе нулевого значения потенциальной энерги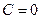и и 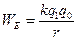(3.7). В этой формуле q₁ и q₀ – электрические заряды точечных тел, а не их модули, поэтому 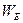- алгебраическая величина.

Рассмотрите самостоятельно движение точечного тела с электрическим зарядом q₀ по прямой, соединяющей точечные тела с электрическими зарядами q₁ и q₀ при различных знаках электрических зарядов и убедитесь в неизменности формул (3.3) и (3.7).

2. Потенциал электрического поля. Разность потенциалов. Потенциалом электрического поля в заданной точке называется физическая величина, равная отношению потенциальной энергии точечного тела с электрическим зарядом q₀, находящегося в этой точке, к этому заряду. 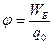(3.8) – математическая запись определения потенциала электрического поля в заданной точке. При перемещении точечного тела с электрическим зарядом q₀ из т.1 в бесконечность в формуле (3.5) 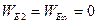и . С учетом этого равенства получаем второе (эквивалентное) определение 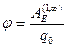(3.9): потенциалом электрического поля в заданной точке называется физическая величина, равная отношению работы, выполненной электрической силой по перемещению точечного тела с электрическим зарядом q₀ из данной точки в бесконечность, к этому заряду. Единицей измерения потенциала электрического поля является 1В (1 Вольт). .

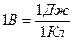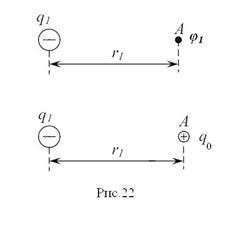Рассмотрим электрическое поле неподвижного точечного тела с электрическим зарядом q₁ и получим формулу для вычисления потенциала электрического поля в заданной точке А. В соответствии с определением (3.8) в точку А нужно поместить точечное тело с электрическим зарядом q₀ (рис.22). Подставим формулу (3.7) в определение (3.8): 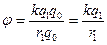. 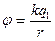(3.9) – формула для вычисления потенциала электрического поля неподвижного точечного тела с электрическим зарядом q₁ в заданной точке этого поля. В этой формуле r – расстояние от точечного тела с электрическим зарядом q₁ до заданной точки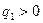. При , при 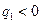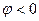, то есть 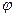- алгебраическая величина. Из формулы (3.9) видно, что потенциал электростатического поля в заданной точке не зависит от модуля и знака электрического заряда q₀ точечного тела, расположенного в этой точке. Этот вывод справедлив для любого электростатического поля. Потенциал электростатического поля в заданной точке – это скалярная характеристика этого поля.

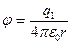– второй вариант формулы (3.9) для вычисления потенциала электрического поля неподвижного точечного тела с электрическим зарядом q₁ в заданной точке поля.

Величина 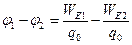(3.10) называется разностью потенциалов электростатического поля. С учетом (3.5) преобразуем равенство (3.10) к виду 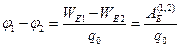. Формула 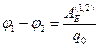(3.11) является математической записью определения разности потенциалов электростатического поля: разностью потенциалов электростатического поля называется физическая величина, равная отношению работы, выполненной электрической силой при перемещении точечного тела с электрическим зарядом из первой точки электростатического поля во вторую, к этому заряду.

Если разность потенциалов известна в каждой точке электростатического поля, то из определения (3.11) 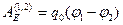(3.12) – формула для вычисления работы электрической силы 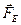при перемещении точечного тела с электрическим зарядом q₀ из точки электростатического поля с потенциалом в точку с потенциалом 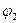. Формулу (3.12) можно преобразовать к виду 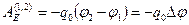(3.13). Работа электрической силы для двух близких точек в электростатическом поле 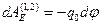(3.14).

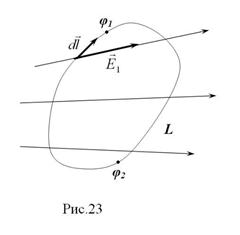
Рассмотрим замкнутый контур L в электростатическом поле. Для точек с потенциалами и 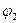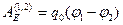, где q₀ – электрический заряд точечного тела, перемещаемого по части контура L. При обходе всего контура, очевидно, 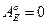, так как 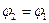. Эту же работу 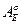при обходе точечного тела с электрическим зарядом q₀ по контуру L можно вычислить иначе: 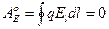(3.15). Из (3.15) 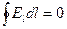(3.16). Величина 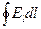называется циркуляцией вектора 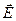по замкнутому контуру L. Циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

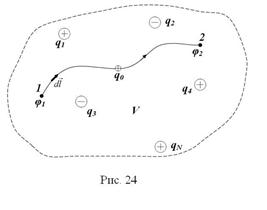
Рассмотрим работу электрической силы при перемещении точечного тела с электрическим зарядом q₀ в электростатическом поле системы точечных тел с электрическими зарядами q₁, q₂, … ,q_N из т.1 этого поля в т.2 (рис.24). В соответствии с принципом суперпозиции 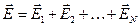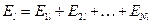(3.17), где 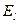– проекция вектора 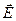на малое перемещение 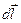. Работа силы 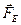при переходе точечного тела с электрическим зарядом q₀ из т.1 в т.2 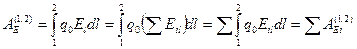(3.18). Работы 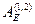и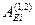вычислим по формуле (3.12):

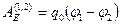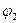(3.19), где и – потенциалы электростатического поля системы тел с электрическими зарядами в точках 1 и 2 этого поля.

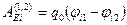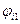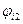(3.20),где и – потенциалы электростатического поля точечного тела с электрическим зарядом 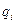в точках 1 и 2, если бы в объеме V было только это точечное тело с номером i в своем неизменном положении в этом объеме. Подставляя (3.19) и (3.20) в (3.18), получаем 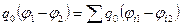. Из этого равенства 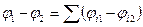. Данное равенство преобразуем к виду 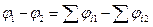(3.21). Из (3.21) следует, что 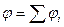(3.22): потенциал электростатического поля системы точечных тел с электрическими зарядами в заданной точке поля равен сумме потенциалов электростатических полей в этой точке, которые были бы при отдельном поочередном расположении каждого из тел при условии, что отдельное расположение каждого тела в объеме V идентично его расположению в этом объеме в системе тел.

3. Связь напряженности электростатического поля с потенциалом.Электростатическое поле можно описать либо с помощью векторной величины 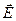, либо с скалярной величины 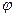. Очевидно, что эти величины должны быть связаны друг с другом.

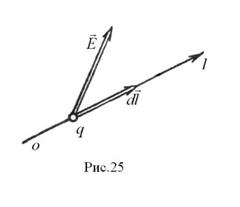Выберем в пространстве, в котором имеется электростатическое поле, произвольную ось оl (рис.25). При перемещении точечного тела с электрическим зарядом q вдоль этой оси на 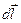электрическая сила выполняет работу 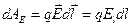(здесь Е_l – проекция 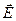на 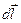). В соответствии с формулой (3.14) 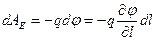(мы написали частную производную, поскольку 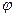, вообще говоря, изменяется не только при перемещении вдоль оси оl, но также и при перемещениях в других направлениях). Приравняв оба выражения для работы, получим соотношение 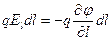, после сокращения на q следует, что 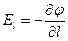(3.23).

Таким образом, проекция вектора 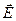на ось оl равна скорости убывания потенциала при перемещении вдоль этой оси.

Рассмотрев направления вдоль координатных осей x, y, z, получим выражения 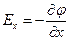, , 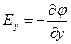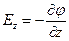(3.24).

Так как 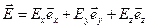, то для вектора 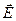получаем выражение .

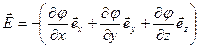Величина, стоящая в скобках, представляет собой градиент функции 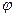. Следовательно, мы приходим к формуле 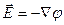(3.25), согласно которой напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком.

С помощью (3.25) можно, зная функцию , найти напряженность поля в каждой точке поля. Можно решить и обратную задачу: зная функцию , найти разность потенциалов между двумя произвольными точками поля. Для этого воспользуемся тем, что работа А_Е, выполняемая силой 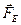поля при перемещении точечного тела с электрическим зарядом q по произвольной траектории из точки 1в точку 2: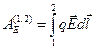. Вместе с тем в соответствии с (3.12) эта работа 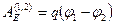. Приравняв оба выражения и сократив на q, придем к соотношению 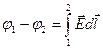(3.26). Интеграл можно брать по любой линии, соединяющей точки 1и 2, ибо работа силы электростатического поля не зависит от пути.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется поверхностью равного потенциала или эквипотенциальной поверхностью. Ее уравнение имеет вид 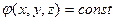. (3.27)

При перемещении по касательной к эквипотенциальной поверхности на отрезок 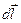потенциал не изменяется (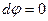). Согласно формуле (3.3) проекция вектора 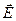на касательную к поверхности равна нулю. Отсюда следует, что вектор 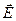направлен по нормали к поверхности. Приняв во внимание, что вектор 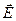направлен по касательной к

линии 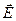, заключаем, что линии напряженности в каждой точке ортогональны к эквипотенциальным поверхностям.

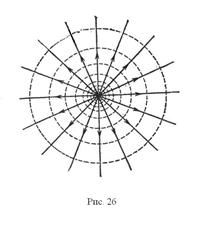
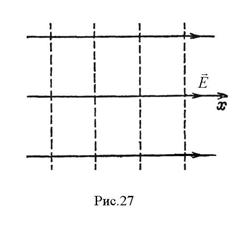Эквипотенциальную поверхность можно провести через любую точку поля. Однако целесообразно проводить поверхности так, чтобы разность потенциалов между соседними поверхностями была всюду одна и та же (например, 1В). Тогда по густоте эквипотенциальных поверхностей можно судить о модуле напряженности поля — там, где поверхности гуще, потенциал изменяется вдоль линии поля быстрее и, следовательно, напряженность поля больше; там, где поверхности реже, напряженность поля меньше.

На рис.26 изображены линии 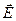(сплошные) и линии пересечения эквипотенциальных поверхностей с плоскостью чертежа (штриховые) для поля точечного тела с электрическим зарядом. На рис.27 изображена аналогичная картина для однородного поля.

Легко сообразить, что потенциал однородного поля с напряженностью 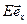имеет вид 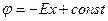(3.28). Константу в этом выражении нельзя выбрать так, чтобы потенциал в бесконечности обращался в нуль. Такой выбор возможен только в том случае, если напряженность поля убывает с расстоянием достаточно быстро для того, чтобы был конечным (1— произвольная точка поля).

Дата добавления: 2014-03-11; просмотров: 906; Нарушение авторских прав

Мы поможем в написании ваших работ!