Структура регрессивной модели

Необходимо учесть ранее накопленный опыт для выдвижения гипотезы о форме связи между целевым параметром Y и входным фактором X_i (i=1.. k), т.е о структуре математической модели.

Выбираем фиксированную точку факторного пространства, т.е. при конкретных значениях факторов, значения выходного параметра равно математическому ожиданию:

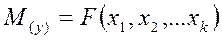(1)

Функция, связывающая мат. ожидание некоторой случайной величины с другими переменными, называется регрессией.

Очень часто мат. ожидание целевого параметра представляют в виде полинома.

У каждого целевого параметра есть своя способность влиять на регрессию – коэффициент регрессии β.

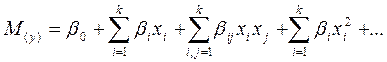(2)

Полиномом 2 можно описать с наперед заданной точностью любую функцию, непрерывную в какой-либо области факторного пространства.

Простейшим видом модели такого типа является линейная регрессионная модель:

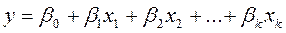(3)

Уравнение (3) записано в случае исключения нелинейных слагаемых в уравнении (2).

Статистическая математика кроме линейной регрессионной модели может быть выражена через степенную регрессионную модель

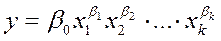(4)

Дата добавления: 2014-03-11; просмотров: 291; Нарушение авторских прав

Мы поможем в написании ваших работ!