
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Функционально полные системы
ЛЕКЦИЯ 13.
Процесс контроля
Заключительный контроль
При текущем контроле используется обратная связь в ходе проведения самих работ для того, чтобы достичь требуемых целей и решить возникающие проблемы прежде, чем это потребует слишком больших затрат.
В рамках заключительного контроля обратная связь используется после того, как работа выполнена.
Хотя заключительный контроль осуществляется слишком поздно, чтобы отреагировать на проблемы в момент их возникновения, он имеет две важные функции.
Одна из них состоит в том, что заключительный контроль дает руководству организации информацию, необходимую для планирования в том случае, если аналогичные работы предполагается проводить в будущем.
Вторая функция заключительного контроля состоит в том, чтобы способствовать мотивации. Если руководство организации связывает мотивационные вознаграждения с достижением определенного уровня результативности, то очевидно, что фактически достигнутую результативность надо измерять точно и объективно.
В процессе контроля есть три этапа: выработка стандартов и критериев, сопоставление с ними реальных результатов и принятие необходимых корректирующих действий.
Опр1: Система логических функций S называется функционально полной (ФПС) (набор, базис), если любая логическая функция может быть выражена формулой над S.
Таким образом, можно говорить, что {И, ИЛИ, НЕ} – Булев базис
Если система Y выражает функции S - ФПС, то Y тоже ФПС и S сводится к Y. Данное утверждение является частным случаем замыкания ФПС.
Опр2: Замыкание ФПС S– это множество ПФ, которые можно получить суперпозицией функций из S. Обозначение: [S].
Ясно, что [S] – есть множество всех ПФ, где S={И, ИЛИ, НЕ}.
Теорема: S, Y- некоторые множества ПФ, тогда
1. SÍ[S]
2. [[S]]=[S]
3. SÍY, следовательно [S]Í[Y]
4. [S]=множество логических функций
5. S- базис и SÍ[Y], значит Y - базис.
Док-во: 1)-4) исходят из определения базиса. 5) SÍ[Y]Þ[S]Í[[Y]](см 3.), [S]Í[Y] (см 1.), т.к. S - базис, то [S]=множество логических функцийÞ(см 4.) [Y]=множество логических функций.
Система S - ФПС в слабом смысле, если любая логическая функция представима в виде суперпозиции функций из S и констант 0 и 1.
Примеры базисов ПФ:
{И, ИЛИ, НЕ} базис Буля
{И, НЕ} конъюнктивный базис ((НЕа) ИЛИ(НЕв)=НЕ(а И в)
{ИЛИ, НЕ} дизъюнктивный базис ((НЕа) И (НЕв)=НЕ(а ИЛИ в)
{И, +, 1} базис Жегалкина (НЕ а=а+1)
{|} базис Шиффера (a|в=НЕ(ав); НЕа =a|в; ав=НЕ(a|в)=(а|в)|(в|а))
{¯} базис Пирса (a¯в=НЕ(аИЛИв); НЕа =a¯в; аИЛИв=НЕ(a¯в)=(а¯в) ¯ (в¯ а))
Отметим, что конъюнктивный базис является минимальным логическим базисом.
Рассмотрим базис Жегалкина. Основные тождества алгебры Ж:
А+в=в+а
А(в+с)=ав+ас
А+а=0
А+1=НЕа
А+0=а
А ИЛИ в=НЕ(НЕа И НЕв)=(а+1)(в+1)+1=а+в+ав.
Теорема: любая ПФ представима полиномом Жегалкина.
Док-во: т.к алгебра Ж имеет базис, а все функции базиса Буля представимы через этот базис и одну и ту же функцию описывают равносильные формулы, то между алгебрами Буля и Жегалкина устанавливается взаимно-однозначное соответствие.
Опр3: Система логических функций называется замкнутым классом, если любая суперпозиция функций из S снова лежит в S, т.е S=[S].
Пример: А={НЕ, ПРЯМОТА} – замкнутый класс, т.к. НЕ(ПРЯМОТА)=НЕ, НЕ(НЕ)=ПРЯМОТА
Примеры замкнутых классов:
1) функции, сохраняющие константы:
S0={f | f(0,0,…,0)=0} ПР: дизъюнкция
S1={f | f(1,1,…,1)=1}; ПР: конъюнкция
2) 

 самодвойственные функции: S*={f | f(x1…xn)= f(x1…xn)};
самодвойственные функции: S*={f | f(x1…xn)= f(x1…xn)};
3) монотонные функции: S£= {f | a£b Þf(a)£f(b)}, где a=(a1…an), b=(b1…bn) , a£b= {"i ai£bi};
4) линейные функции: Sл={f | f=Saixi Ågi},описанные линейным полиномом Жегалкина.
Как же определить, является ли система ПФ базисом?
Теоремы о функциональной полноте
Теорема 1. S - ФПС в слабом смысле, если она содержит хотя бы одну немонотонную или нелинейную функцию.
Теорема 2 (Теорема Поста). S - ФПС тогда и только тогда, когда она содержит:
1) нелинейную функцию,
2) немонотонную функцию,
3) несамодвойственную функцию,
4) функцию, не сохраняющую констант.
Док-во: необходимость. От противного: пусть есть хотя бы одна из перечисленных функций, тогда их замыкания совпадают с самими базисами, т.е. через этот базис невозможно выразить остальные функции, т.е. допущение неверно.
Достаточность. 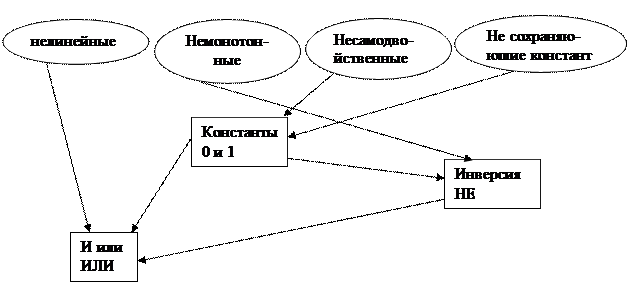
| <== предыдущая страница | | | следующая страница ==> |
| Текущий контроль | | |
Дата добавления: 2014-03-11; просмотров: 538; Нарушение авторских прав

Мы поможем в написании ваших работ!