Проецирование точки

Точка, как математическое понятие, не имеет размеров. Очевидно, если объект проецирования является нульмерным объектом, то говорить о его проецировании бессмысленно.

В геометрии под точкой целесообразно принимать физический объект, имеющий линейные измерения. Условно за точку можно принять шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.

При построении ортогональных проекций точки следует руководствоваться первым инвариантным свойством ортогонального проецирования: ортогональная проекция точки есть точка.

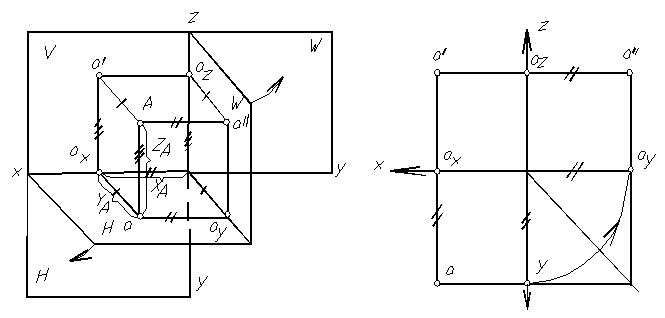
Положение точки в пространстве определяется тремя координатами: X, Y, Z, показывающие величины расстояний, на которые точка удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно определить точки встречи этих прямых с плоскостями проекций и измерить соответству-

Рис. 1.9 Рис. 1.10

ющие величины, которые укажут соответственно значения абсциссы X , ординаты Y и аппликаты Z точки (рис. 1.10).

Проекцией точки является основание перпендикуляра, опущенного из точки на соответствующую плоскость проекций. Горизонтальной проекцией точки а называют прямоугольную проекцию точки на горизонтальной плоскости проекций, фронтальной проекцией а ^/ – соответственно на фронтальной плоскости проекций и профильной а^// – на профильной плоскости проекций.

Прямые Аа, Аa ^/ и Аa ^// называются проецирующими прямыми. При этом прямую Аа, проецирующую точку А на горизонтальную плоскость проекций, называют горизонтально- проецирующей прямой, Аa ^/ и Аa ^// - соответственно: фронтально и профильно-проецирущими прямыми.

Две проецирующие прямые, проходящие через точку А определяют плоскость, которую принято называть проецирующей.

При преобразовании пространственного макета, фронтальная проекция точки А – а ^/ остается на месте, как принадлежащая плоскости, которая не меняет своего положения при рассматриваемом преобразовании. Горизонтальная проекция – а вместе с горизонтальной плоскостью проекции повернется по направлению движения часовой стрелки и расположится на одном перпендикуляре к оси Х с фронтальной проекцией. Профильная проекция - a ^// будет вращаться вместе с профильной плоскостью и к концу преобразования займет положение, указанное на рисунке 1.10. При этом - a ^// будет принадлежать перпендикуляру к оси Z , проведенному из точки а ^/ и будет удалена от оси Z на такое же расстояние, на какое горизонтальная проекция а удалена от оси Х. Поэтому связь между горизонтально и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков аа_y и а_y a ^// и сопрягающей их дуги окружности с центром в точке пересечения осей ( О – начало координат). Отмеченной связью пользуются для нахождения недостающей проекции ( при двух заданных). Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено с помощью прямой, проведенной под углом 45⁰ из начала координат к оси Y ( эту биссектрису называют прямой k – постоянной Монжа). Первый из указанных способов предпочтителен, как более точный.

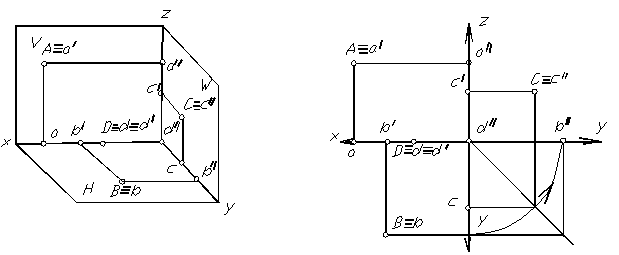
Рис. 1.11 Рис.1.12

Из этого следует:

1. Точка в пространстве удалена:

от горизонтальной плоскости H на величину заданной координаты Z,

от фронтальной плоскости V на величину заданной координаты Y,

от профильной плоскости W на величину координаты .X.

2. Две проекции любой точки принадлежат одному перпендикуляру (одной линии связи):

горизонтальная и фронтальная – перпендикуляру к оси X,

горизонтальная и профильная – перпендикуляру к оси Y,

фронтальная и профильная – перпендикуляру к оси Z.

3. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Из этого следует – по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью проекцию .

Если точка имеет три определенные координаты, то такую точку называют точкой общего положения. Если у точки одна или две координаты имеют нулевое значение, то такую точку называют точкой частного положения.

На рисунке 1.11 дан пространственный чертеж точек частного положения, на рисунке 1.12 – комплексных чертеж (эпюр) этих точек. Точка А принадлежит фронтальной плоскости проекций, точка В – горизонтальной плоскости проекций, точка С – профильной плоскости проекций и точка D – оси абсцисс (Х ).

Дата добавления: 2014-04-16; просмотров: 601; Нарушение авторских прав

Мы поможем в написании ваших работ!