Реологические модели массива

Реологические модели отражают свойство ползучести (течения) горных пород, т.е. их способность деформироваться во времени при постоянном напряжении.

Существуют вязкоупругие и вязкопластические реологические модели. Обе включают в себя вязкий элемент Ньютона в виде поршня в цилиндре с вязкой жидкостью.

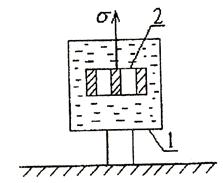
Рис. 7.5. Вязкий элемент Ньютона

1 – цилиндр тс вязкой жидкостью; 2 – поршень с отверстиями

Согласно закону Ньютона в вязком элементе напряжения пропорциональны скорости деформации (скорости смещения слоев вязкой жидкости).

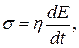(7.10)

где 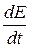- скорость деформации (градиент скорости смещения слоев); 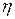- коэффициент вязкости, Па×с.

Одна из наиболее распространенных вязкоупругих моделей, модель Максвелла.

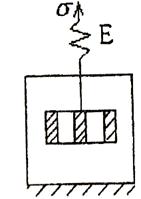
Рис. 7.6. Структурная модель Максвелла

Модель Максвелла состоит из пружины, т.е. упругого элемента и последовательно соединенного с ней вязкого элемента Ньютона. Напряжения, приложенные к структурной модели, вызывают в начальный момент мгновенную упругую деформацию пружины, соответствующую закону Гука. В дальнейшем деформация системы растет с постоянной скоростью в результате поддавливания жидкости через отверстия поршня.

Скорость деформации среды 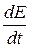складывается из скорости упругой деформации 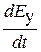и скорости вязкой деформации .

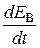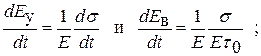(7.11)

отсюда получаем

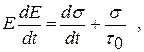(7.12)

где 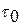– период релаксации напряжения в данном теле, т.е. время, в течении которого напряжения в теле уменьшаются в e = 2,72 раза.

При 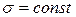процесс деформации принимает процесс ползучести и предыдущее уравнение примет вид

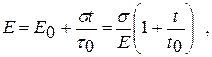(7.13)

где 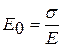– произвольная постоянная, или упругая деформация в начальный момент времени.

Следовательно, рост деформации при постоянном напряжении идет по линейному закону.

Вязкопластические модели учитывают развитие во времени упругих, пластических и вязких деформаций.

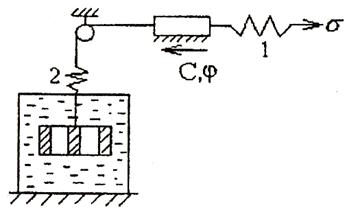
Рис. 7.7. Структурная схема вязкопластической модели Шведова.

Общая деформация такой среды под действием приложенной нагрузки равна

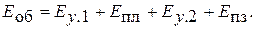(7.14)

Дата добавления: 2014-05-04; просмотров: 331; Нарушение авторских прав

Мы поможем в написании ваших работ!