Проверка математической модели на адекватность

Проверка полученного уравнения регрессии на адекватность дает ответ на вопрос, можно ли использовать полученное линейное уравнение или необходима более сложная модель. Проверка на адекватность представляет собой оценку ошибки аппроксимации изучаемого процесса полученным уравнением регрессии. Проверка на адекватность проводится при помощи критерия Фишера.

Опытное значение критерия Фишера:

,

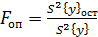где остаточная дисперсия опытов;

общая дисперсия опытов.

Остаточная дисперсия вычисляется по формуле:

,

где – расчетные построчные значения функции отклика;

– опытные построчные средние значения функции отклика;

N – число строк в матрице планирования;

d – число значащих коэффициентов регрессии.

Теоретическое значение критерия Фишера определяется по таблице приложения при числах степеней свободы f₁=N-d; f₂=N’-1.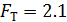

4.1 Остаточная дисперсия:

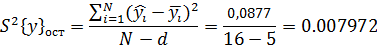
4.2 Общая дисперсия, вычисленная ранее:

4.3 Опытное значение критерия Фишера

Таблица 6. Определение остаточной дисперсии

№	x0	x1	x2	x3	x4	b0x0	b1x1	b2x2	b3x3	b4x4
	+	+	+	+	+	0,936167	0,03167	0,01529	0,01308	0,00827	1,003477	0,86566	0,13781	0,018991596
	+	+	+	+	-	0,936167	0,03167	0,01529	0,01308	-0,00807	0,987137	0,87466	0,11247	0,012649501
	+	+	+	-	+	0,936167	0,03167	0,01529	-0,01108	0,00827	0,979317	0,88633	0,092984	0,008646024
	+	+	+	-	-	0,936167	0,03167	0,01529	-0,01108	-0,00807	0,962977	0,89533	0,067644	0,004575711
	+	+	-	+	+	0,936167	0,03167	-0,01329	0,01308	0,00827	0,974897	0,865	0,109897	0,012077351
	+	+	-	+	-	0,936167	0,03167	-0,01329	0,01308	-0,00807	0,958557	0,92	0,038557	0,001486642
	+	+	-	-	+	0,936167	0,03167	-0,01329	-0,01108	0,00827	0,950737	0,912	0,038737	0,001500555
	+	+	-	-	-	0,936167	0,03167	-0,01329	-0,01108	-0,00807	0,934397	0,937	0,002603	6,77561E-06
	+	-	+	+	+	0,936167	-0,02767	0,01529	0,01308	0,00827	0,944137	0,92666	0,01747	0,000305201
	+	-	+	+	-	0,936167	-0,02767	0,01529	0,01308	-0,00807	0,927797	0,93233	0,004536	2,05753E-05
	+	-	+	-	+	0,936167	-0,02767	0,01529	-0,01108	0,00827	0,919977	0,94433	0,024356	0,000593215
	+	-	+	-	-	0,936167	-0,02767	0,01529	-0,01108	-0,00807	0,903637	0,95366	0,05003	0,002503001
	+	-	-	+	+	0,936167	-0,02767	-0,01329	0,01308	0,00827	0,915557	0,95133	0,035776	0,001279922
	+	-	-	+	-	0,936167	-0,02767	-0,01329	0,01308	-0,00807	0,899217	0,961	0,061783	0,003817139
	+	-	-	-	+	0,936167	-0,02767	-0,01329	-0,01108	0,00827	0,891397	0,97666	0,08527	0,007270973
	+	-	-	-	-	0,936167	-0,02767	-0,01329	-0,01108	-0,00807	0,875057	0,98466	0,10961	0,012014352
∑	0,08773853

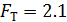> следовательно модель не адекватна и необходимо искать модель более высокого порядка или уменьшать интервал варьирования.

Дата добавления: 2014-07-10; просмотров: 352; Нарушение авторских прав

Мы поможем в написании ваших работ!