Дифференциальное и полное сечение рассеяния

Для количественного описания процесса столкновения или процесса рассеяния частицы на неподвижном центре вводится понятие дифференциального эффективного сечения рассеяния. Пусть в начале координат находится рассеивающий неподвижный центр, а налетающая частица движется, имея прицельный параметр r, и рассеивается на угол c. Частицы движущиеся изначально в пределах площадки

ds=2prdr (2)

рассеиваются в телесный угол

dW=2psincdc (3)

Дифференциальное сечение определяется как модуль отношения ds/dW. Нетрудно получить следующее соотношение

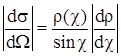(4)

Это соотношение справедливо для классической механики. В квантовой механике решение задачи о рассеянии ищется в виде суммы падающей и рассеяной волн

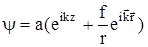(5)

где f - амплитуда рассеяния, зависящая от угла. Для дифференциального сечения имеет место следующее соотношение

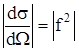(6)

Следует отметить, что в случае, когда рассеивающий центр не обладает сферической симметрией (например рассеивающей частицей является молекула, обладающая дипольным моментом), дифференциальное сечение, вообще говоря, зависит не только от полярного, но и от азимутального угла j. Однако в экспериментах как правило измеряется усредненное по углу j сечение и именно оно представляет практический интерес для анализа газоразрядных процессов, поскольку молекулы газа ориентированы случайным образом относительно потока заряженных частиц.

Полным сечением или просто сечением называется следующая величина

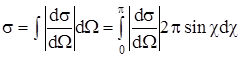(7)

Физический смысл величины s следующий: это площадь круга, попадая в который налетающая частица испытывает рассеяние. Ясно, что величина s будет конечной если сила взаимодействия рассеивающего центра и налетающей частицы обращается в 0 на некотором конечном расстоянии R от силового центра и, очевидно, что для полного сечения будет справедливо следующее соотношение

s=pR² (8)

Если же взаимодействие является дальнодействующим (а в классической механике это практически всегда так и есть) и сила взаимодействия спадает до 0 лишь при R ® ¥, то для полного сечения имеет место проблема расходимости. Действительно, даже если частица летит на большом прицельном расстоянии от центра все равно она испытает рассеяние хотя бы на малый угол.

Едва ли не единственным исключением является т.н. взаимодействие твердых (или еще говорят идеально упругих) шаров, испытывающих рассеяние только лишь при непосредственном контакте. Пусть имеется неподвижный твердый шар радиусом r₂ и налетающий шар с радиусом r₁ . Нетрудно сообразить, что для того чтобы столкновение произошло центр налетающего шара должен попасть в площадку

s = p(r₁ + r₂)². (9)

Вот эта величина и является полным сечением для столкновени двух твердых шаров. Модель твердых шаров используется в газокинетической теории для оценки величины сечений. В частности для случая взаимодействия электрона с атомом можно пренебречь размером электрона и получить, что сечение равно

s = pr₂², (10)

где r₂ - радиус атома, а для случая взаимодействия двух одинаковых атомов r₁ = r₂ или иона с атомом получаем

s = pd², (11)

где d - диаметр атома. Разумеется полученные соотношения могут быть использованы только для грубых оценок, а не точных расчетов. В то же время газокинетические сечения являются характерным масштабом, с которым удобно проводить сравнения. Например когда говорят, что сечение того или иного процесса мало или велико, то имеется в виду, что оно намного меньше или больше, чем соответствующее газокинетическое сечение.

Возможность существенного отличия реального сечения от газокинетического связана, в частности, с квантовомеханическими эффектами. Отметим, что эти эффекты приводят к тому, что в квантовой механике ситуация с расходимостью полного сечения отличается от классической механики. Оказывается s является конечным, если потенциал взаимодействия убывает с расстоянием быстрее, чем 1/r . В противном случае s расходится.

Дата добавления: 2014-07-14; просмотров: 911; Нарушение авторских прав

Мы поможем в написании ваших работ!