МОДЕЛИРОВАНИЕ ЭКОНОМИКИ. ЛАБОРАТОРНАЯ РАБОТА №6 ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ ТАРИФЫ

Как s_тр, так и s являются микроскопическими величинами, характеризующими индивидуальный акт столкновения рассеиваемой и рассеивающей частиц. Для описания движения ансамбля налетающих частиц в среде состояшей из множества рассеивающих частиц вводятся так называемые макроскопические характеристики. В частности, в теории переноса вводится так называемое макроскопическое сечение

S = ns, (14)

где n - плотность рассеивающих частиц, т.е. их число в одном см³. Нетрудно видеть, что величина S имеет размерность см^-1, и, соответственно, величина

l=1/S = 1/ns (15)

имеет размерность см. Эту величину называют длиной свободного пробега и, как мы сейчас покажем, она представляет собой среднее расстояние проходимое частицей от одного столкновения до другого.

Пусть имеется объем V₀ и в нем N₀ частиц, тогда n = N₀/V₀. Вероятность для одной из этих частиц попасть в некоторый объем V внутри V₀ равна V/V₀, вероятность, что ее там нет (1-V/V₀). Соответственно, вероятность того, что в V вообще нет частиц (1-V/V₀)^Nо. С другой стороны вероятность w(х) для налетающей частицы пройти путь x без столкновений равна вероятности того, что в объеме V=sx нет ни одной частицы. Тогда получаем

w(х) = (1-sх/V₀)^Nо = (1- nsх/N₀)^No ~ exp(-nsx) (16)

Вероятность пройти без столкновений путь х + dх

w(х+dх) = exp(-sn(х+dх)) (17)

Следовательно вероятность dР(х) пройти от одного столкновения до другого путь в пределах от х до х+dх равна

dР(х) = w(х) - w(х+dх) = exp(-nsx) (1- exp(-nsdх)) ~

~ еxp(-nsx)(1- 1+nsdх)) = exp(-nsx)nsdх. (18)

Или иначе

dР(х) =exp(-x/l)dх/l (19)

Вычисляем средний пробег

<x> = 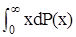= = 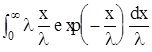l 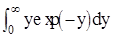=l, (20)

что и требовалось доказать.

Введем еще несколько макроскопических характеристик. Поделив средний пробег на скорость налетающей частицы v получим среднее время между столкновениями.

t = l/v = 1/nsv (21)

Соответственно, величина обратная к t

n = 1/t = v/l = nsv (22)

есть не что иное как среднее число столкновений, испытываемых частицей в единицу времени, или частота столкновений. Отметим, что если скорости налетающих и рассеивающих частиц сравнимы между собой, то в соотношениях (21) и (22) под величиной v следует понимать среднюю относительную скорость их движения. Для ансамбля атомов или молекул, распределение которых по скоростям описывается Максвелловской функцией средняя скорость относительного движения

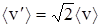, (23)

где

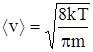(24)

это средняя тепловая скорость молекул. Соответственно, для частоты столкновений молекул друг с другом в модели твердых шаров можно получить следующее соотношение

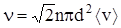. (25)

В более точной модели, учитывающей то, что сечение зависит от относительной скорости частиц, при вычислении частоты столкновений необходимо проводить усреднение сечения

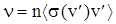. (26)

Все введенные макроскопические характеристики тем или иным образом связаны с микроскопическим полным сечением. Аналогичным образом вводятся макроскопические характеристики, связанные с транспортным сечением. Чтобы отличать эти характеристики от характеристик, связанных с полным сечением, к ним обычно прибавляют определение эффективная. Например

n_эф = ns_трv (23)

это эффективная частота столкновений, а

l_эф = 1/ns_тр (24)

это эффективная длина свободного пробега. Вспоминая физический смысл величины s_тр можно сказать, что l_эф это характерное расстояние пройдя которое частица существенно отклонится от первоначального направления движения. Соответственно

t_эф = 1/ns_трv (25)

это характерное время, по истечении которого частица испытает “эффективное столкновение” и отклонится на большой угол.

Впрочем поскольку полное сечение зачастую расходится и физический смысл имеет только транспортное сечение и связанные с ним величины, то слово эффективная иногда опускается. Если s конечная величина, то вспоминая, что s_тр = s(1-<соsc>) можно получить связь между частотой и эффективной частотой в следующем виде.

n_эф = n(1-<соsc>). (26)

Следует заметить, что поскольку характер взаимодействия может быть различным, то макроскопические характеристики можно определить для каждого вида взаимодействия: например длина свободного пробега до ионизации

l_i = 1/ns_i

или частота упругих столкновений

n_упр = ns_упрv .

Отметим, что сечение неупругих процессов всегда конечная величина, так как очевидно, что частицы, находящиеся на большом расстоянии друг от друга и слабовзаимодействующие, не могут изменить внутреннее состояние друг друга.

МОДЕЛИРОВАНИЕ ЭКОНОМИКИ. ЛАБОРАТОРНАЯ РАБОТА №6 ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ ТАРИФЫ

Интернет-провайдер обслуживает две категории пользователей со следующими функциями спроса на трафик:

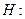
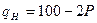
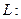
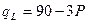
Количество пользователей одинаково, 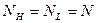. Себестоимость 1Мб трафика для провайдера равна 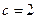. Разработать оптимальную стратегию ценообразования при различных предположениях.

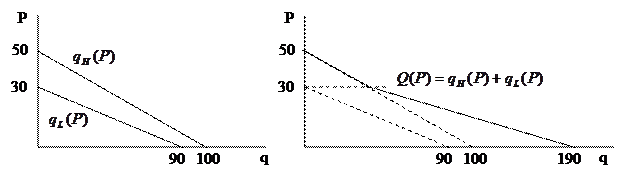1. Предположим, что продавец не может дискриминировать покупателей и устанавливает для всех общую цену за 1 Мб трафика. Найти оптимальную цену.

2. Предположим, компания может использовать линейный тариф, при котором цена за единицу продукции устанавливается на уровне издержек производства и устанавливается фиксированная абонентская плата за предоставление интернет-услуг. Найти оптимальный размер абонентской платы.

3. Теперь ответим на вопрос: оптимально ли устанавливать цены на 1Мб на уровне издержек производства? Для этого необходимо найти оптимальную цену за Мб (Р) и размер абонентской платы (F), максимизирующей прибыль при условии, что обслуживаются все потребители.

4. Теперь рассмотрим случай, когда компания может устанавливать различные тарифные планы, состоящие из комбинации фиксированной платы и платы за 1 Мб с тем, чтобы потребители имели возможность выбрать более подходящий для них план. Найти оптимальные значения Р и F для этих тарифных планов.

Дата добавления: 2014-07-14; просмотров: 341; Нарушение авторских прав

Мы поможем в написании ваших работ!