
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция №4 Тема: «Химическая, нефтеперерабатывающая и деревообрабатывающая промышленность»
Этот метод позволяет строить схемы различного порядка точности. Схемы Рунге-Кутта очень удобны как для расчетов на ЭВМ, так и для «ручных» расчетов. Сейчас они являются наиболее употребительными в практических вычислениях.
Построим семейство схем второго порядка точности и на его примере разберем основные идеи метода. В качестве исходного выражения возьмем ряд Тейлора
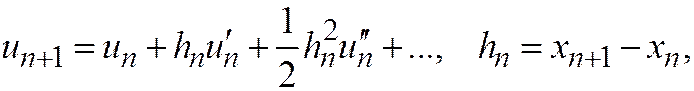 (20.1)
(20.1)
удерживая в нем член О(h2), порядок которого равен предполагаемому порядку точности схемы. Чтобы избежать дифференцирования функции f(x,u), заменим производную 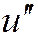 конечной разностью. Так как первая производная
конечной разностью. Так как первая производная 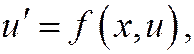 то вторая производная
то вторая производная 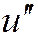 будет равна
будет равна
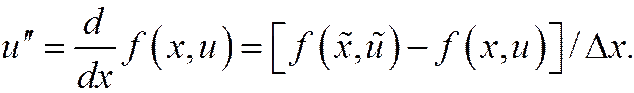
Соответственно выбирая значения 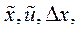 после такой замены второй член в (20.1) можно формально объединить с первым, приведя (20.1) к следующему виду
после такой замены второй член в (20.1) можно формально объединить с первым, приведя (20.1) к следующему виду
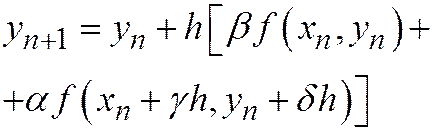 (20.2)
(20.2)
(поскольку эта схема для расчета приближенного решения, мы снова употребляем обозначение уn вместо un). Здесь 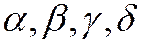 - параметры, значения которых следует определить. Рассматривая правую часть (20.2) как функцию от h, разложим ее в ряд по степеням шага h
- параметры, значения которых следует определить. Рассматривая правую часть (20.2) как функцию от h, разложим ее в ряд по степеням шага h
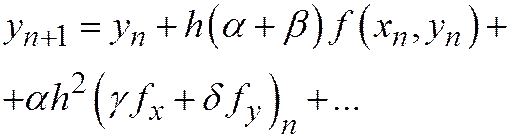 .
.
Выберем параметры 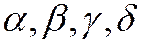 так, чтобы это разложение было возможно более близко к ряду Тейлора (20.1). Очевидно, можно правильно передать два первых члена формулы Тейлора, если положить
так, чтобы это разложение было возможно более близко к ряду Тейлора (20.1). Очевидно, можно правильно передать два первых члена формулы Тейлора, если положить

Действительно 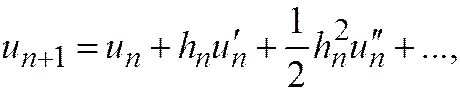 значит при
значит при 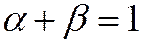
получаем второе слагаемое, а так как 
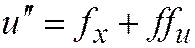 , то при
, то при 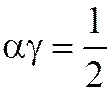 получаем fx и для получения ffu надо положить
получаем fx и для получения ffu надо положить  .
.
Для определения четырех параметров получено только три уравнения, так что один параметр остается свободным. Выражая через 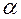 остальные параметры и подставляя их в (20.2), получим однопараметрическое семейство двучленных схем Рунге-Кутта
остальные параметры и подставляя их в (20.2), получим однопараметрическое семейство двучленных схем Рунге-Кутта
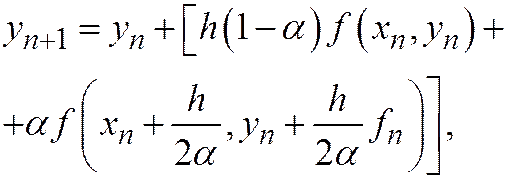 (20.3)
(20.3)
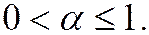
Выбрать параметр 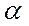 так, чтобы схема (20.3) правильно передавала и третий член формулы Тейлора (20.1), невозможно.
так, чтобы схема (20.3) правильно передавала и третий член формулы Тейлора (20.1), невозможно.
Погрешность этой схемы можно исследовать так же, как было сделано для схемы ломаных. При этом доказывается следующий результат. Если f(x,u) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по схеме (20.3), равномерно сходится к точному решению с погрешностью О(max h2n), т.е. двучленная схема Рунге-Кутта имеет второй порядок точности.
Формула (20.3) имеет неплохую точность и нередко используется в численных расчетах. При этом обычно полагают либо 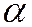 =1, либо
=1, либо 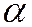 = ½.
= ½.
|
В первом случае получается схема особенно простого вида
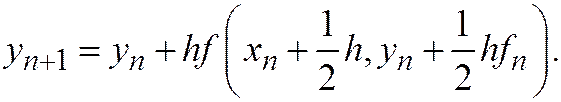 (20.4)
(20.4)
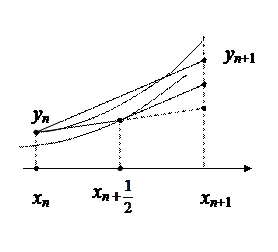
Ее смысл поясняется на рис. 20.1. Сначала делаем половинный шаг по схеме ломаных, находя 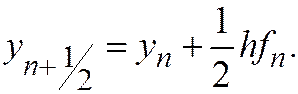 Затем в найденной точке определяем наклон интегральной кривой
Затем в найденной точке определяем наклон интегральной кривой  По этому наклону определяем приращение функции на целом шаге
По этому наклону определяем приращение функции на целом шаге 
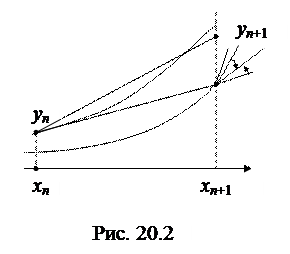
Геометрическая интерпретация второго случая изображена на рис. 20.2
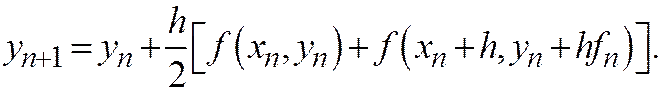
Здесь мы сначала грубо вычисляем по схеме ломаных значение функции 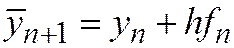 и наклон интегральной кривой
и наклон интегральной кривой 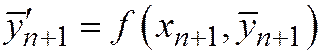 в новой точке. Затем находим средний наклон на шаге h:
в новой точке. Затем находим средний наклон на шаге h: 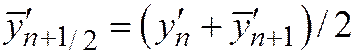 и по нему уточняем значение уn+1. Схемы такого типа называются «предиктор-корректор».
и по нему уточняем значение уn+1. Схемы такого типа называются «предиктор-корректор».
В таблице 20.1 приведен численный расчет по схеме (20.4) того же примера, который рассмотрен на прошлой лекции и приведен в таблице 19.1.
Таблица 20.1
| xn | yn | u(x) | Схема ломанных при h = 0,25 | |
| h = 1 | h = 0,5 | |||
| 0,5 1,0 | - 0,25 | 0,031 0,317 | 0,042 0,350 | 0,016 0,220 |
Таблица 20.1 заполняется следующим образом:
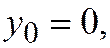 пусть
пусть 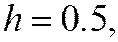 тогда
тогда
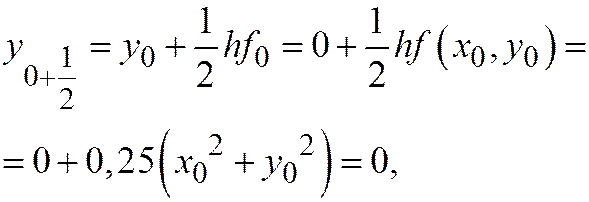
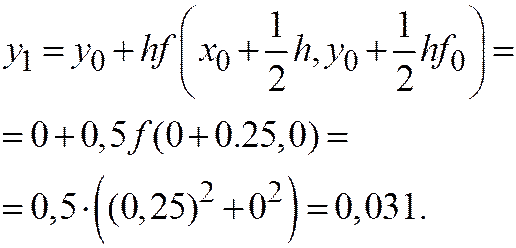
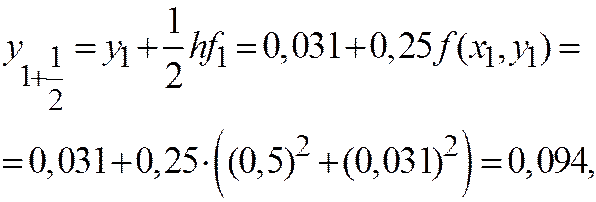
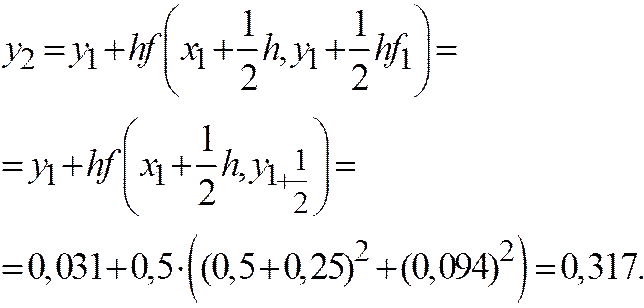
Из таблицы видно, что схема второго порядка точности дает существенно лучшие результаты, чем схема ломаных. Уже расчет на грубой сетке с h = 0,5 можно считать удовлетворительным.
Методом Рунге-Кутта можно строить схемы различного порядка точности. Например, схема ломаных 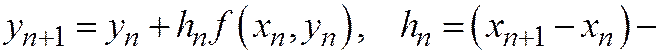 есть схема Рунге-Кутта первого порядка точности. Наиболее употребительны схемы четвертого порядка точности, образующие семейство четырехчленных схем. Приведем без вывода ту из них, которая записана в большинстве стандартных программ ЭВМ
есть схема Рунге-Кутта первого порядка точности. Наиболее употребительны схемы четвертого порядка точности, образующие семейство четырехчленных схем. Приведем без вывода ту из них, которая записана в большинстве стандартных программ ЭВМ
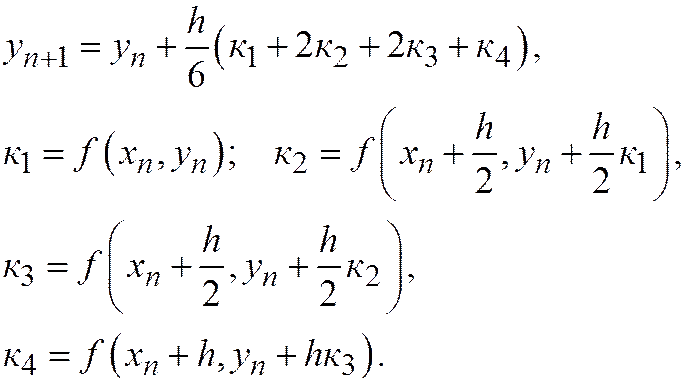 (20.5)
(20.5)
Схемы Рунге-Кутта имеют ряд важных достоинств:
а) все они (кроме схемы ломаных) имеют хорошую точность;
б) они являются явными, т.е. значение уn+1 вычисляется по ранее найденным значениям за определенное число действий по определенным формулам;
в) все схемы допускают расчет с переменным шагом, значит нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае;
г) для начала расчета достаточно выбрать сетку хn и задать значение 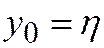 .
.
Далее вычисления идут по одним и тем же формулам. Все эти свойства схем очень ценны при расчетах на ЭВМ.
На случай систем уравнений схемы Рунге-Кутта легко переносятся, как во всех других методах, при помощи формальной замены y, f(x,y) на Y, F(x,y). Нетрудно произвести покомпонентную запись этих схем. Например, для системы двух уравнений
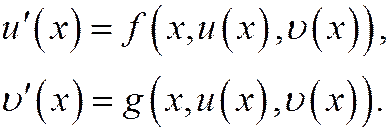
Обозначая через у, z приближенные значения функций u(x), 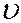 (x), запишем аналогичную (20.5) четырехчленную схему следующим образом
(x), запишем аналогичную (20.5) четырехчленную схему следующим образом
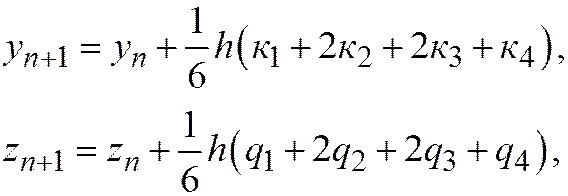
где
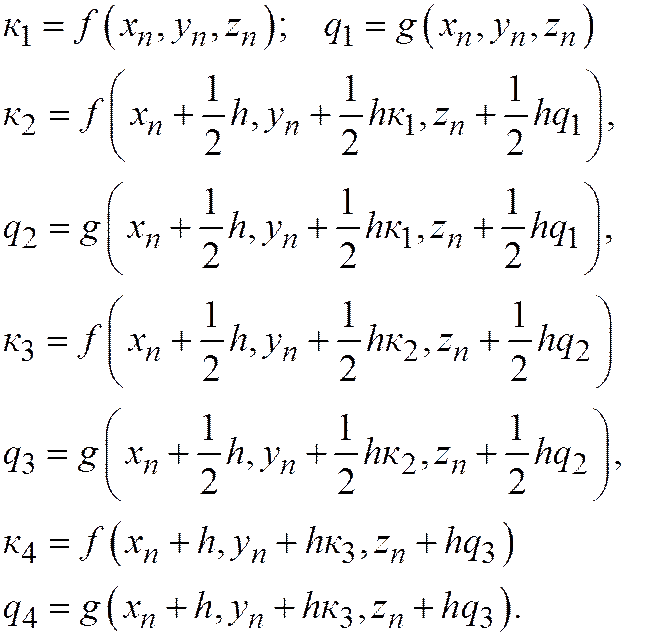
Погрешности (или остаточные члены) различных схем Рунге-Кутта связаны с максимумами модулей соответствующих производных f(x,u) громоздкими выражениями. Например, для схемы Эйлера формула выглядит следующим образом (мы ее c Вами выводили)
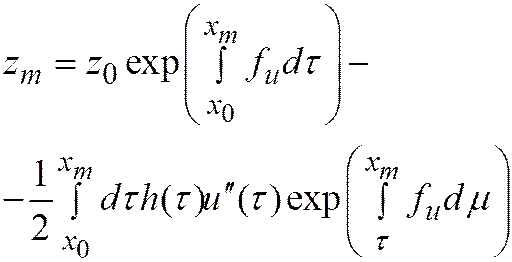 . 20.6)
. 20.6)
Наглядное представление о величине погрешностей можно получить в одном частном случае, когда f = f (x). При этом дифференциальное уравнение сводится к квадратуре, а все схемы численного интегрирования переходят в квадратурные формулы. Действительно, схема 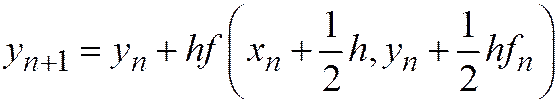 переходит в формулу средних. В самом деле, имеем уравнение
переходит в формулу средних. В самом деле, имеем уравнение 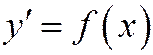 , интегрируем его в пределах от xn от xn+1
, интегрируем его в пределах от xn от xn+1 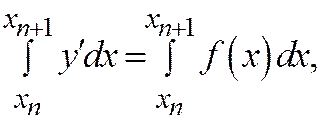 получаем:
получаем:  . Это формула средних.
. Это формула средних.
Схема 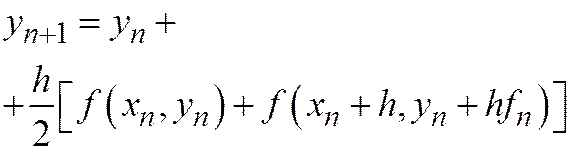 переходит в формулу трапеций. Схема Рунге-Кутта четвертого порядка
переходит в формулу трапеций. Схема Рунге-Кутта четвертого порядка 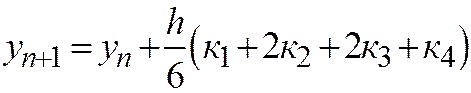 переходит в формулу Симпсона с шагом h/2.
переходит в формулу Симпсона с шагом h/2.
Напомним, что мажоранты остаточных членов этих формул на равномерной сетке с указанными шагами соответственно равны
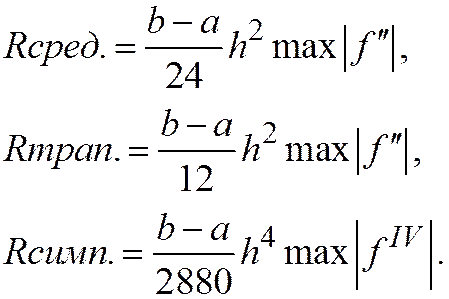 (20.7)
(20.7)
Численные коэффициенты в остаточных членах (20.7) малы; это является одной из причин хорошей точности схем Рунге-Кутта.
Какими из формул Руте-Кутта целесообразно пользоваться в каждом конкретном случае и как выбирать шаг сетки?
Если правая часть дифференциального уравнения непрерывна и ограничена вместе со своими четвертыми производными (и эти производные не слишком велики), то хорошие результаты дает схема четвертого порядка - благодаря очень малому коэффициенту в остаточном члене и быстрому возрастанию точности при уменьшении шага. Если же правая часть не имеет указанных производных, то предельный порядок точности этой схемы не может реализоваться. Тогда не худшие (хотя, по-видимому, и не лучшие) результаты дают схемы меньшего порядка точности, равного порядку имеющихся производных; например, для двукратно непрерывно дифференцируемых правых частей – схемы второго порядка точности.
Шаг сетки следует выбирать настолько малым, чтобы обеспечить требуемую точность расчета; других ограничивающих шаг условий в методе Рунге-Кутта нет. Но выражения остаточных членов типа (20.6) слишком громоздки; поэтому априорными оценками точности для выбора шага в практических расчетах не пользуются. Удобнее делать расчеты со сгущением сетки, давая апостериорную оценку точности.
Встречаются важные задачи, в которых функции являются достаточно гладкими, но настолько быстро меняющимися, что схемы Рунге-Кутта как низкого, так и высокого порядка точности требуют неприемлемо малого шага для получения удовлетворительного результата. Такие задачи требуют использования (а нередко – разработки) специальных методов, ориентированных на данный узкий класс задач.
Лекция №4 Тема: «Химическая, нефтеперерабатывающая и деревообрабатывающая промышленность»
Время 2 часа
Вступление (5 минут)
Основные вопросы:
1.Характеристика химической промышленности. Технология производства изделий из пластмасс (14 минут)
2. Нефтеперерабатывающая промышленность (14 минут)
3.Общая характеристика деревообрабатывающей промышленности (14 минут)
4.Технологии лесозаготовительных и деревообрабатывающих производств.(14 минут)
5.Химическая переработка древесины (14 минут)
Выводы (5 минут)
Основные понятия: химическая технология, химико-технологические системы, химико-технологические процессы, полимеры, пластмассы, лесное хозяйство, лесозаготовка, лесопильная рама, кругопильные станки, ленточные станки, лобзиковые станки, пиролиз, гидролиз.
Литература
Основная:
1.Желібо Є.П., Анопко Д.В., Буслик В.М., Авраменко М.А., Петрик Л. С., Пирч В.П. Основи технологій виробництва в галузях народного господарства: Навч.посібник. – К.: Кондор, 2005. – 716 с.
2.Система технологий. Учеб. пособие /Под ред. П. Д. Дупко – Х.: Бурин кника, 2003. – 336 с.
Дополнительная:
1. Боровский Б.И., Тимченко З.В. Методические указания по изучению дисциплины «Основы отраслевых технологий» - Симферополь, 2000. - 108 с.
2.Боровский Б.И., Мозговой А.И., Тимченко З.В. Развитие технологий производства. - Симферополь, 1996.
3.Экономика предприятия: Учебник /Под ред. С.Ф.Покропивного - К.: КНЭУ, 2003. – 606 с.
г. Симферополь, 2007г
Вступление
Основными тенденциями современного развития химической промышленности является переход к непрерывным, автоматизированным, безотходным, энергосберегающим производствам с широким использованием биотехнологических процессов. Современные химические технологии направлены, в первую очередь, на решение глобальных проблем человечества: сбережение и пополнение продовольственных запасов переработкой непищевого сырья, энергосбережения и предупреждения загрязнения биосфери.
Предприятия химического комплекса относятся к сложным межотраслевых производств, которые определяющий влияют на развитие большинства других масштабных отраслей: горно - химической и металлургической промышленности, энергетики и нефтепереработки, агропромислового комплекса, пищевой, легкой и фармацевтической промышленность.
Научно- технологической базой химической промышленности являются химические технологии и химическое машиностроение.
Предприятия химического комплекса Украины производят свыше 130000 разных химических продуктов и принадлежат к важнейшим отраслям ее производительных сил.
Химическая промышленность обеспечивает другие отрасли полупрод Лесопромышленный комплекс Украины включает лесохозяйственный, деревообрабатывающий, целлюлозно-бумажный, лесохимический подкомплексы.
Лесохозяйственный комплекс состоит из двух подотраслей: лесного хозяйства и лесозаготовительной промышленности.
Лесное хозяйство занимается лесовосстанавлением (лесничество) и лесозаготовкой.
Цель лекции сформировать у студентов представление о химической и нефтехимической промышленности и деревообрабатывающей промышленности, определить особенности и перспективы развития в Украине, охарактеризовать технологию производства изделий из пластмасс, технологию перегонки нефти, технологий лесозаготовки, лесопильного производства, производства фанеры, столярно - мебельного производства, а также определение методов химической переработки древесины, способов используемых в целлюлозно-бумажной промышленности и при производстве бумаги и картона.
Для этого необходимо решить следующие задачи:
- сформировать представление о химической и нефтеперабатывающие отраслях промышленности, рассмотреть основные их технологии;
- определить основные особенности этих отраслей промышленности в Украине.
- сформировать систему знаний о деревообрабатывающей промышленности;
- сформировать представление о технологиях лесозаготовительных и деревообрабатывающих производств;
- развить память и активизировать мышление.
| <== предыдущая страница | | | следующая страница ==> |
| Лекция 2. МЕТОД РУНГЕ-КУТТА РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ | | | Характеристика химической промышленности. Технология производства изделий из пластмасс |
Дата добавления: 2014-07-19; просмотров: 530; Нарушение авторских прав

Мы поможем в написании ваших работ!