Корреляционный и регрессионный анализ

В агрономических исследованиях чаще всего встречаются такие соотношения между переменными, когда каждому значению признака Х соответствует не одно, а множество возможных значений признака У, т.е. их распределение. Такие связи, обнаруживаемые лишь при массовом изучении признаков, в отличии от функциональных (когда каждому значению одной величины соответствует строго определённое значение другой) называются вероятностными, или корреляционными.

Корреляционные связи характеризуются двумя основными показателя- ми – теснотой связи и формой связи. Для измерения тесноты и формы связи используют статистические методы, называемые корреляцией и регрессией.

Зависимость называется корреляционной, если с увеличением средней величины первого признака увеличивается средняя величина второго, или, наоборот, с увеличением средней величины первого признака второй уменьшается. В первом случае корреляция и регрессия – прямая, или положительная, во втором – обратная, или отрицательная (направление корреляции). По форме корреляция и регрессия может быть линейной и криволинейной. Корреляцию и регрессию называют простой,или парной, если исследуется связь между двумя признаками, и множественной, когда изучается зависимость между тремя и более признаками.

Регрессиейназывают изменение результативного признака У (функции) при определённом изменении одного или нескольких факториальных (аргументов). Связь между функцией и аргументом выражается уравнением регрессии, или корреляционным уравнением. При простой регрессии уравнение кратко обозначается У=f(X) и при множественной У=f (X, Z, V…). Для оценки тесноты (силы) связи используют коэффициенты корреляции и корреляционное отношение.

Линейная корреляция – это такая зависимость между двумя признаками Х и У, которая носит линейных характер и выражается уравнением приямой линии У = а+вХ. Это уравнение называется уравнением регрессии У на Х, а соответствующая ему прямая линия – выборочной линией регрессии У на Х. Линейная регрессия – это такая зависимость, когда при любом значении аргумента Х одинаковые приращения его вызывают одинаковые изменения функции У. Когда при одинаковых приращениях аргумента функция имеет неодинаковые изменения, регрессия называется криволинейной.

В агрономии большинство связей криволинейные. Однако некоторые из них близки к линейным и их удобней анализировать как линейные зависимости, вычисляя коэффициент корреляции (r) – числовой показатель простой линейной корреляции, указывающий на тесноту (силу) и направление связи Х с У. Данный показатель рассчитывается по формуле:

.

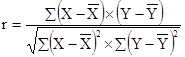Значение коэффициента корреляции лежит в пределах от +1 до -1. Если

r = 0,0 – корреляция отсутствует;

r £ 0,3 – корреляция слабая;

r = 0,3-0,7 – корреляция средняя;

0,7 < r <1,0 – корреляция тесная (сильная);

r = 1,0 – корреляция полная (функциональная зависимость).

Квадрат коэффициента корреляции (r²) называется коэффициентом детерминации и обозначается d_УХ. Он показывает долю (%) тех изменений, которые в данном явлении зависят от изучаемого фактора.

Дата добавления: 2014-07-23; просмотров: 657; Нарушение авторских прав

Мы поможем в написании ваших работ!