Моделирование реологического поведения пищевых материалов

Проводить лабораторные работы на натуральных биотехнологических продуктах с различной структурой от жидкообразной до твердообразной, включая вязко-пластичные, пластичные и упруго-эластичные системы по определению комплекса их реологических характеристик (сдвиговых, компрессионных, поверхностных), не всегда представляется возможным. Дороговизна и малая

стойкость биотехнологических продуктов при хранении вынуждают в исследо­вательской

практике отходить от натуральных материалов и заменять их модельными органическими веществами, которые достаточно полно воспроизводили бы наиболее существенные свойства натурального продукта в определенном технологическом процессе.

Моделирование как метод изучения различных процессов может быть физическим и математическим, основанным на теории подобия. В реологии распространен метод моделей. Существенные реологические свойства могут быть фундаментальными (упругость, пластичность и вязкость) и сложными (комбинация фундаментальных свойств). Совокупность существенных реологических свойств может быть представлена при помощи идеальных тел. Из них три тела рассматриваются в классической механике сплошных сред (твердое тело Гука, пластическое тело Сен-Венана, реальная жидкость - тело Ньютона). Сложные тела можно получить комбинацией соответствующих простых.

В реологии различают два взаимоисключающих понятия: «твёрдое идеально-упругое тело» и «невязкая жидкость». Под первым понимается такое тело, равновесные форма и напряжение которого достигаются мгновенно. Жидкость называется невязкой, т.е. если жидкость не способна создавать и поддерживать напряжения сдвига. Между предельными состояниями тел - идеальноупругими твёрдыми телами и невязкими жидкостями - существует огромное многообразие тел промежуточного характера.

Модели абсолютно твёрдого, упруго деформирующегося твёрдого гуковского тела и истинной ньютоновской жидкости являют собой представление о двух противоположных положениях в реологии. Многочисленные экспериментальные факты не укладываются в эти простейшие концепции и дают в итоге «нестандартную» картину поведения материалов - проявление вязкоупругости реальных тел. Вязкоупругие свойства проявляются, например, в том, что внезапно приложенное и поддерживаемое неизменным напряженное состояние вызывает мгновенную деформацию, сопряженную с упругим откликом, вслед за чем следует процесс вязкого течения, который может быть ограниченным и неограниченным во времени. При этом поведение вещества определяется не только текущим напряженным состоянием, но и всеми прошлыми состояниями, то есть вещество обладает свойством, которое называют эффектом памяти («динамической памятью состояния»). Степень преобладания упругих или вязких свойств определяется продолжительностью внешнего воздействия (числом Деборы).

С понятием вязкоупругости связано понятие механической релаксации - эффекта, проявляющегося в уменьшении во времени напряжения, создавшего в теле деформацию. Механическая релаксация приводит к ряду других эффектов: ползучести, гистерезисным явлениям при деформировании и т. д. Напряжения в жидкости релаксируют от начального значения до нулевого, поскольку напряжения в неподвижной жидкости сохраняться не могут. В твёрдом же теле всегда сохраняются некоторые остаточные (равновесные) напряжения, сколь долго не продолжалась бы релаксация. Это различие также может быть принято для определения различия между твёрдым и жидким телом. Однако оно не всегда столь же очевидно на практике. Релаксация может происходить настолько медленно, что наблюдатель может посчитать её оконченной и зафиксировать некое остаточное напряжение; а тело меж тем будет продолжать релаксировать. Скорость релаксации количественно характеризуется временем релаксациитр. Его значение характеризует скорость приближения состояния тела к равновесному.

В случае, когда напряжение не уменьшается со временем, а поддерживается постоянным, реальные вязкоупругие реологические тела могут проявлять ещё одно свойство - ползучесть.

Ползучесть материалов (последействие) — изменение с течением времени деформации твёрдого тела под воздействием постоянной нагрузки или механического напряжения. Ползучесть материалов экспериментально изучают прежде всего при простых напряженных состояниях: одноосных растяжении, сжатии, а также чистом сдвиге. Условия проведения таких экспериментов определены нормативной документацией (ГОСТами). Ползучесть описывается кривой ползучести, которая представляет собой зависимость деформации от времени при постоянных температуре и приложенной нагрузке (или напряжении).

Следует отметить, что описание поведения тел с помощью моделей становится некорректным, если упругие или вязкие свойства вещества являются нелинейными. Аксиомой реологии можно считать положение о том, что любой реальный материал обладает всеми реологическими свойствами, выраженными в разной степени.

Рассмотрим основные модели, которые могут встретиться при изучении реологических свойств пищевых масс. При этом необходимо указать, что точные математические закономерности получены только для ньютоновских жидкостей, для всех неньютоновских течений получены только приближённые формулы.

Известны три промежуточные модели идеализированных тел:

• идеально-упругое тело (Гука);

• идеально-вязкая жидкость (Ньютона);

• идеально-пластичное тело (Сен-Венана).

Идеально-упругое тело Гука (модель - пружина, рис. 13а). В таком теле энергия, затраченная на деформацию, накапливается и может быть возвращена при разгрузке. Закон Гука описывает поведение кристаллических и аморфных твёрдых тел при малых деформациях, а также жидкостей при изотропном расширении-сжатии.

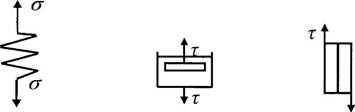
а б в

а) идеально-упругое тело Гука; б) идеально-вязкая жидкость Ньютона; в) идеально-пластичное тело Сен-Венана

Рисунок 13 - Модели идеализированных реологических тел

Идеально-вязкая жидкость Ньютона характеризуется тем, что в ней напряжения пропорциональны скорости деформации. Вязкое течение происходит под действием любых сил, как бы малы они не были; однако скорость деформации снижается при уменьшении сил, а при их исчезновении обращается в ноль. Для таких жидкостей вязкость, являющаяся константой, пропорциональна напряжению сдвига.

Закон Ньютона описывает поведение многих низкомолекулярных жидкостей при сдвиге и продольном течении. Механическая модель ньютоновской жидкости (рис. 13б) представляет собой демпфер (устройство для гашения - демпфирования - колебаний или предотвращения механических колебаний, возникающих в машинах и приборах при их работе), состоящий из поршня, который перемещается в цилиндре с жидкостью. При перемещении поршня жидкость через зазоры между поршнем и цилиндром протекает из одной части цилиндра в другую. При этом сопротивление перемещению поршня пропорционально его скорости.
Идеально пластичное тело Сен-Венана может быть представлено в виде элемента, состоящего из двух прижатых друг к другу пластин (рис. 13в). При относительном перемещении пластин между ними возникает постоянная сила трения, не зависящая от сжимающей их силы. Тело Сен-Венана не начнёт деформироваться до тех пор, пока напряжения сдвига не превысят некоторого критического значения - предела текучести (предельного напряжения сдвига), после чего элемент может двигаться с любой скоростью.

Для того чтобы описать реологическое поведение сложного тела в зависимости от свойств его компонентов, можно комбинировать в различных сочетаниях рассмотренные выше модели простейших идеальных тел, каждое из которых обладает лишь одним физико-механическим свойством. Эти элементы могут быть скомбинированы параллельно или последовательно.

Основными сложными моделями являются: упруго-пластичное тело;

вязкоупругие тела Кельвина - Фойга и Максвелла; вязко-пластические тела Бингама, Шведова и Шведова - Бингама.

Модель упруго-пластического тела (рис. 14а) получается при последовательном соединении упругого элемента Гука с модулем упругости G и пластического элемента Сен-Венана с пределом текучести 0_т. При О < О_т происходит упругая деформация материала, а при О = От - пластическое течение.

а б в

а) модель упруго-пластического тела; б) модель вязкоупругого тела Кельвина - Фойгта; в) модель вязкоупругого релаксирующего тела Максвелла

Рисунок 14 - Сложные модели реологических тел

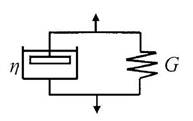
Вязко-упругое тело Кельвина - Фойгта представлено механической моделью, полученной при параллельном соединении упругого элемента Гука с модулем упругости G и вязкого элемента Ньютона с вязкостью h (рис. 14б). Под действием растягивающего усилия пружина удлиняется, а поршень будет

85

двигаться в жидкости. Это движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пружины наступает не сразу. Когда нагрузка устранена, пружина сжимается до первоначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.

Для написаний математической модели тела Кельвина - Фойгта используют то обстоятельство, что при параллельном соединении элементов деформация сложного тела gm равна деформации каждого элемента, а напряжение суммарного элемента ©кф равно сумме напряжений в отдельных элементах ©г и ©н. Окончательная математическая модель тела Кельвина - Фойгта выглядит следующим образом:

© = G-g+ T]-f,

где G - модуль упругости при сдвиге, Па; g- угловая деформация; h - ньютоновская вязкость, Па-с.

Модель тела Кельвина - Фойгта отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после её снятия.

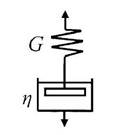
Механическая модель вязко-упругого релаксирующего тела Максвелла (рис. 16в) представляет собой последовательное соединение элементов Гука с модулем упругости G и Ньютона с вязкостью h На оба элемента действует одинаковое напряжение.

Тело Максвелла ведёт себя как упругое или вязкое в зависимости от отношения времени релаксации материала к длительности эксперимента. Если под действием мгновенного усилия пружина растягивается, а затем сразу нагрузка снята, то поршень не успевает двигаться и система ведёт себя как упругое тело. Однако, с другой стороны, если поддерживать растяжение пружины постоянным, она постепенно релаксирует, перемещая поршень вверх, и система ведёт себя как ньютоновская жидкость.

Реологическое уравнение тела Максвелла имеет вид:

g' = ©/G +©/h,

где © - напряжение, Па;

g' - скорость деформации.

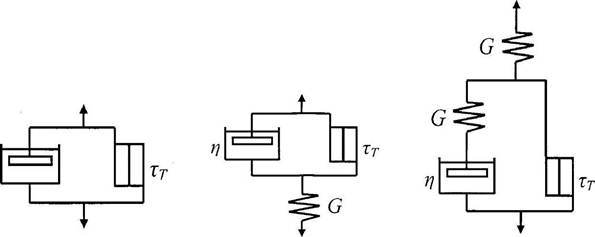
а б в

а) модель вязкопластичного тела Шведова - Бингама;

б)модель вязко-пластичного тела Бингама; в)модель вязко-пластичного тела Шведова Рисунок 15 - Сложные модели реологических вязко-пластичных тел

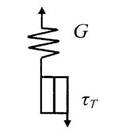
Двухэлементная механическая модель вязко-пластичного тела Шведова - Бингама (рис. 15а) состоит из соединённых параллельно элементов Ньютона с вязкостью h и Сен-Венана с пределом текучести 0т. Если 0 < 0т, то система ведёт себя как абсолютно твёрдое недеформированное тело. Реологическое уравнение этого тела имеет вид:

g' = (0- 0т)/^

В природе имеются материалы, которые в первом приближении можно рассматривать как тело Сен-Венана. Они начинают течь, когда напряжение сдвига достигает предельного значения. Если нет вязкого сопротивления, то скорость течения материала станет сколь угодно большой. Это показывает, что такие материалы могут только в первом приближении рассматриваться как тела Сен- Венана. Во втором приближении они должны обладать вязкостью. Всё это приводит к постулированию идеального тела Бингама, сочетающего упругость, вязкость и пластичность.

Механическая модель Бингама (рис. 15б) состоит из элементов Гука с модулем упругости G, Ньютона с вязкостью h и Сен-Венана с пределом текучести 0т. Элементы Ньютона и Сен-Венана соединены взаимно параллельно, а вместе - последовательно с элементом Гука. Под действием напряжения 0 < 0т модель

Бингама имеет только упругую деформацию. Реологическое уравнение этой модели при О>От имеет вид:

g' = О/G +(О- 0r)/h.

Механическая модель Шведова состоит из элементов Гука с модулем упругости Gr, Сен-Венана с пределом текучести От и Максвелла с модулем упругости Gм и вязкостью rj (рис. 15в). В 80-х годах 19 века Ф.Н. Шведов изучил релаксационные процессы в коллоидных растворах и впервые обнаружил у них упругость и вязкость. Модель этого тела отличается от модели Бингама тем, что параллельно модели Сен-Венана присоединена модель Максвелла, а у модели Бингама - элемент Ньютона. При О < От деформация модели Шведова происходит только благодаря элементу Гука. При О > От деформируются все элементы модели. Реологическое уравнение модели Шведова в дифференциальной форме имеет вид:

g' = О■ (1/Gr + Шм) + (О- От)/г.

Стремление исследователей более точно отобразить поведение пищевых материалов под нагрузкой привело к созданию сложных моделей, что значительно увеличило трудоемкость расчетов. Модели, имеющие малое число элементов, редко дают удовлетворительную сходимость опытных данных с рассчитанными по уравнениям. В тоже время увеличение количества элементов сверх четырёх не приводит к существенному качественному изменению модели, так как модели, содержащие до четырёх элементов включительно, исчерпывают всё разнообразие механического поведения данного материала.

Моделирование деформационного поведения пищевых материалов можно проводить не только на основе механических моделей, но и электрических. При этом напряжение сопоставляют с э.д.с. электрической цепи, скорость деформации - с электрическим током, модуль упругости - с обратной величиной ёмкости, а вязкость - с сопротивлением. Последовательное соединение элементов механиче­ской модели эквивалентно параллельному соединению элементов электрической цепи, а параллельное в механической модели - последовательному соединению в электрической. Электрическое моделирование позволяет применять моделирующие ЭВМ при изучении упруго-вязко-пластичных свойств пищевых материалов, а также при расчёте процессов их переработки.

Добиться качественных, а тем более количественных соотношений натуры и модели, меняя число и последовательность соединения элементов, затруднительно. Кроме того, метод моделей уводит от изучения молекулярных взаимодействий в объекте, подменяя это феноменологическими способами. Подобие модели и образца имеет место при подобии условий однозначности и равенстве определяющих критериев. При моделировании процессов вынужденного движения вязко-пластичных или пластично-вязких систем должны быть соблюдены условия гидродинамического подобия. В настоящее время разработан ряд приемов упрошенного физического моделирования, успешно применяемых в практике экспериментов. Одним из них является замена реальных рабочих сред модельными средами. Этот метод широко используют при градуировке приборов водой, касторовым маслом, сахарным раствором. В качестве модельных материалов пищевых сред экспериментаторы используют гра­фитную массу, мелко измельчённую увлажнённую бумажную массу, бетонитовую глину, иловую и торфяную грязь.

Для исследований указанные модельные материалы представляют собой хорошие заменители натурального продукта, обеспечивая идентичные с биотехнологическими продуктами изменения свойств в зависимости от одинаковых переменных параметров. Подобные замены обусловлены высокой стоимостью как самих биотехнологических сред, так и некоторых модельных материалов.

Таким образом, для приобретения практических навыков по определению реологических (структурно-механических) характеристик биотехнологических сред с различной структурой (жидкообразные, вязко-пластичные, твердообразные - пластичные, упруго-эластичные) можно использовать отдельные дисперсные системы с различной концентрацией твердой фазы. Графическая и математическая обработка полученного экспериментального материала с одним, двумя и тремя переменными позволит закрепить приобретенные на практических занятиях данные по выбору вида уравнения и определению эмпирических коэффициентов с различной точностью вычисления.

Дата добавления: 2014-02-26; просмотров: 1394; Нарушение авторских прав

Мы поможем в написании ваших работ!