Экономия числа разрядов можно определить по формуле

log₂ (1/0.628) = 0,67 разряда

Рассмотренный пример позволяет сделать вывод, что при одинаковом качестве в системе передачи на основе ДИКМ можно использовать на 2/3 разряда меньше, чем в системе с обычной ИКМ.

Кодеры и декодеры ДИКМ могут быть выполнены множеством способов в зависимости от разделения функций обработки сигнала между аналоговыми и цифровыми цепями. В одном крайнем случае функции дифференцирования (формирования разностного сигнала) и интегрирования могут быть реализованы посредством аналоговых цепей, в то время как в другом крайнем случае вся обработка сигналов может быть выполнена цифровым способом, а на вход поступают отсчеты в форме обычного ИКМ сигнала.

В системах ДИКМ с аналоговым дифференцированием и интегрированием аналого-цифровому преобразованию подвергается разностный сигнал, а цифро-аналоговому в цепи обратной связи – непосредственно кодовая комбинация разностного сигнала, имеющая ограниченный диапазон. Для интегрирования используются аналоговые суммирующие и запоминающие устройства.

Находят применение системы с ДИКМ, где интегрирование выполняется в цифровой форме. Кодовая комбинация разностного сигнала вместо непосредственного преобразования снова в аналоговую форму в цепи обратной связи подвергается суммированию и накапливается в регистре для получения цифрового представления предыдущего входного отсчета. Затем для получения из цепи обратной связи аналогового сигнала, применяемого для вычитания, используется цифро-аналоговый преобразователь на полный динамический диапазон сигнала.

В связи с достижениями в технологии интегральных микросхем с большой степенью интеграции (БИС) все большее применение находят системы ДИКМ, где вся обработка сигнала выполняется при помощи цифровых логических схем. Аналого-цифровой преобразователь формирует кодовые комбинации, соответствующие отсчетам с полным амплитудным диапазоном (как в обычной ИКМ), которые затем сравниваются с кодовыми комбинациями предыдущего отсчета, полученными цифровым способом. Отметим, что в этом случае аналого-цифровой преобразователь должен формировать кодовые комбинации во всем динамическом диапазоне входных сигналов, в то время как в предыдущих случаях обрабатываются только разностные сигналы.

Декодеры во всех трех рассмотренных вариантах реализуются точно так хе, как цепи обратной связи соответствующих кодеров. Это связано с тем, что в цепи обратной связи формируется аппроксимация входного сигнала (задержанного на один период дискретизации). Если в тракте передачи ДИКМ сигнала не происходят ошибки, то сигнал на выходе декодера (перед фильтрацией) идентичен сигнал, в цепи обратной связи. Таким образом, чем точнее сигнал в цепи обратной связи повторяет входной сигнал, тем точнее сигнал на выходе декодера повторяет входной сигнал.

Дифференциальная импульсно-кодовая модуляция как система с линейным предсказанием. С более общей точки зрения ДИКМ-кодер представляет собой особого рода линейный предсказатель, когда значения сигнала формируются как взвешенная сумма предшествующих отсчетов сигнала

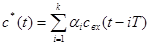, ( 1 )

где с^*(t) – предсказанное значение сигнала в момент времени t; с_вх(t - iT) – отсчет сигнала в момент t – iT, предшествовавший моменту t на i тактовых интервалов; a_i – коэффициенты предсказания, показывающие с каким весом учитываются отсчеты сигналов.

Сигнал в цепи обратной связи кодера ДИКМ представляет предсказание первого порядка значения следующего отсчета, а разность между значениями отсчетов является ошибкой предсказания. В случае предсказания по одному отсчету

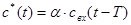. ( 2 ) Разностный сигнал

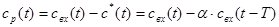. ( 3 )

Дисперсия разностного сигнала

s_р² = s_с² + a ²s_с² – 2R(T)s_c²·a, ( 4 )

где R(T) – значение нормированной функции корреляции сигнала, характеризующей статистическую связь между его значениями, сдвинутыми на интервал дискретизации Т; s_с² – дисперсия сигнала.

Система передачи на основе ДИКМ тем эффективнее, чем меньше значения разностного сигнала. Определим то значение коэффициента предсказания a, при котором дисперсия s_р² минимальна. Взяв производную ds_р² / da , определяем, что a_опт = R(T). В этом случае

s_р² = s_с²[1 – R²(T)] . ( 5 )

При любом отличном от нуля значения R(T) имеет место неравенство вида s_р²< s_с².

Разновидностью разностных методов передачи является ДИКМ, при которой коэффициент предсказания a=1. Физически это означает, что в качестве предсказанного значения сигнала в i –й тактовый момент принимается отсчет сигнала в предыдущий (i – 1)-й момент. В этом случае дисперсия разностного сигнала

s_р²_ДИКМ = 2s_с²[1 – R(T)]. ( 6 ) Дисперсия s_р²_ДИКМ < s_с² при R(T)> 0,5.

Оценим отношение сигнал-шум в разностных системах, считая, что основным источником ошибки является шум квантования. Это справедливо в тех случаях, когда отсутствует перегрузка по крутизне, т.е. когда наибольшая крутизна сигнала s меньше предельно достижимой крутизны его копии s_пред которая равна

s_пред = çc_р ê_макс / Т = d N / T = d N F_д,

где | с_р |_макс – максимальное значение разностного сигнала, связанное с s_р соотношением: | с_р |_макс = k_рs_р, здесь k_р – пик -фактор разностного сигнала;d - шаг квантования и N – общее число шагов квантования для максимального значения разностного сигнала.

В случае оптимального предсказания для ИКМ отношение сигнал-шум будет равно

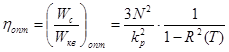, ( 7 )

здесь W_c – мощность сигнала и W_кв – мощность шумов квантования и для ДИКМ

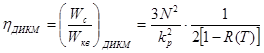. ( 8 )

Отношение W_c / W_кв оказывается тем выше, чем больше корреляция между отсчетами сигнала. Сравнение разностных систем и ИКМ показывает, что при равенстве частот дискретизации и значений пик-фактора показывает, что

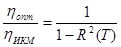и 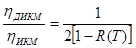, ( 9 ) здесь h_ИКМ – отношение сигнал-шум квантования для обычной ИКМ. При отсут-

ствии корреляции между отсчетами сигнала система с оптимальным предсказанием не тиеет преимуществ перед ИКМ, а ДИКМ обеспечивает меньшее отношение сигнал-шум в 2 раза худшее, чем при ИКМ. При R(T) = 0,5 отношения сигнал-шум при ИКМ и ДИКМ равны. При R(T)> 0,5 ДИКМ имеет преимущество перед ИКМ.

Следовательно, разностная система с оптимальным предсказанием оказывается более эффективной, чем ДИКМ. Однако для реализации оптимального предсказания необходимо знать корреляционную функцию сигнала. Кроме того, предсказатель, построенный в расчете на передачу сигнала одного вида, окажется неэффективным для передачи других сигналов. При ДИКМ не используются никакие априорные сведения о сигнале, и перестройка предсказателя при передаче различных сигналов не требуется.

Теперь выясним, при передаче каких сигналов разностные системы имеют преимущества перед ИКМ и какой получается при этом выигрыш при переходе от ИКМ к разностным методам. Для ответа на эти вопросы необходимо знать корреляционные функции кодируемых сигналов. Допустим, что передаваемый сигнал имеет равномерный спектр в пределах от 0 до w_макс. Такому спектру соответствует нормированная корреляционная функция вида

R(t ) = [sin(w_максt) / (w_максt ).

При частоте дискретизации w _д = 2w_макс корреляционная функция R(t )=0 и применение разностных методов для кодирования таких сигналов нецелесообразно. Величина R(t)> 0 характерна для сигналов, энергетический спектр которых имеет подъем в области низких частот. Для речевого сигнала R(t) приближенно описывается формулой

R(t)=е^{-1140| t |} cos 2980t. ( 10 ) Для телефонного сигнала при частоте дискретизации f_д = 8 кГц согласно (10) получаем R(T)= 0.8/ Подставив это значение в ((9), находим, что выигрыш в отношении сигнал-шум по сравнению с ИКМ при использовании оптимального предсказания составляет примерно 3 раза (менее 5дБ) и при ДИКМ 2,5 раза или около 4дБ, что соответствует экономии 0,67 разряда (рассмотренного ранее примера). Такой выигрыш вряд ли окупает усложнение аппаратуры при передаче телефонных сигналов.

При передаче сигналов звукового вещания, имеющих ту же корреляционную функцию, f_д = 32 кГц. Аналогичные расчеты показывают, что в этом случае выигрыш от применения разностных методов составляет более 15 дБ. Это позволяет уменьшить число разрядов в кодовой комбинации на два-три.

Еще больше оказывается выигрыш при передаче видеосигналов, основная энергия которых сосредоточена в области нижних частот. Доказано, что применение ДИКМ для передачи телевизионных сигналов позволяет с учетом особенностей восприятия видеосигналов уменьшить число разрядов в кодовой комбинации с семи-девяти до четырех-пяти.

Наибольшим искажениям квантования при ДИКМ подвергаются разностные сигналы малой величины. Для уменьшения этих искажений можно применить неравномерное квантование, при котором шаг квантования возрастает по мереувеличения значения разностного сигнала. Такой метод разностного кодирования называется адаптивной дифференциальной импульсно-кодовой модуляцией (АДИКМ), поскольку при этом происходит адаптация величины шага квантования к параметрам кодируемого сигнала.

Дата добавления: 2014-08-04; просмотров: 498; Нарушение авторских прав

Мы поможем в написании ваших работ!