Жесткие и мягкие модели

Рассмотрим механическую систему, состоящую из пружины, закрепленной с одного конца, и груза массой m, прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием x от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (F = − kx) после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:

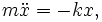
где 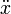означает вторую производную от x по времени: .

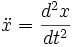Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором».

По формальной классификации эта модель линейная, детерминированная, динамическая, сосредоточенная, непрерывная. В процессе ее построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т.д.), которые в реальности могут не выполняться.

По отношению к реальности это, чаще всего, упрощенная, поскольку опущены некоторые существенные универсальные особенности (например, рассеяние энергии за счет трения). В некотором приближении (пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на её поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведет к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.

При уточнении модели сложность ее математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).

Модель гармонического осциллятора можно применять к объектам, далеким от механики - ее содержательный статус может быть другим (например, при приложении этой модели к биологическим популяциям).

Гармонический осциллятор — пример так называемой «жесткой» модели. Она получена в результате сильной идеализации реальной физической системы. Для решения вопроса о ее применимости необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Иными словами, нужно исследовать «мягкую» модель, получающуюся малым возмущением «жесткой». Она может задаваться, например, следующим уравнением:

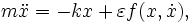
Здесь 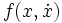— некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения, — некоторый малый параметр. Явный вид функции f нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, результатом решения уравнения гармонического осциллятора могут быть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.

Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

4.2 Классификация математических моделей в зависимости от оператора модели

Любая математическая модель может рассматриваться как некоторый оператор – алгоритм или совокупность уравнений. Наиболее распространенный в математическом моделировании вид оператора – функция. Конкретное задание функции связано с построением математической модели системы – на выбор функции накладываются ограничения, вытекающие из содержательной постановки задачи.

Классификационные признаки при классификации в зависимости от оператора:

- «вид зависимости выходных параметров от значений входных параметров» - линейные или нелинейные модели;

- «вид функциональной зависимости» - алгебраические, дифференциальные (обыкновенные, в частных производных), интегродифференциальные и др. уравнения или системы уравнений.

Линейные и нелинейные модели

Линейность или нелинейность анализируемого процесса оказывает решающее влияние на вид модели, метод программирования.

В основу разработки линейной модели положена гипотеза линейного представления реального нелинейного мира.

Линейная модель - оператор обеспечивает линейную зависимость выходных параметров от входных - линейное соотношение (прямая пропорциональная зависимость) между двумя числовыми переменными.

Модель описывается линейной функцией вида у = кх + в.

Линейная функция нескольких переменных y = a₀ + a₁x₁ +…a_nx_n.

Если задача многомерна – система уравнений.

В линейной модели объекта его параметры связаны линейно - при изменении какого-либо параметра линейное соотношение модели предсказывает линейное изменение зависящего от него выходного параметра, при изменении двух и более параметров - сложение их влияний, линейная модель обладает свойством суперпозиции. Общая реакция системы на входные реакции равна сумме реакций на каждую входную.

Множества входов X, состояний Z и выходов Y – линейные пространства, операторы переходов входов в состояния α и состояний в выходы β – линейные операторы (одновременно однородны и аддитивны).

Использование такой зависимости позволяет описывать многие процессы в реальных системах (это и закон Ньютона и закон Гука в механике, и закон Ома в электротехнике).

Геометрический образ линейной функции, каков бы ни был ее физический смысл, в зависимости от числа независимых переменных — прямая, плоскость. На одинаковые приращения независимой переменной линейная функция (то есть независимо от значения независимой переменной) откликается одинаковыми приращениями. Это означает, что линейная зависимость не обладает избирательностью. Она не может описывать ни резонансных всплесков, ни насыщения, ни колебаний — ничего, кроме равномерного неуклонного роста или столь же равномерного и столь же неуклонного убывания.

В более общем случае, если не учитывается воздействие случайных факторов, а малые изменения входных воздействий приводят к такого же порядка малым изменениям выходного воздействия и состояниям системы, модель можно представить в виде векторного дифференциального уравнения

dy/dt = F(x(t), v(t), g(t) t),

где F – вектор-функция закона функционирования системы; – x, v, h, y - векторы входных, внутренних, управляющих и выходных воздействий соответственно.

В случае линейности систем, когда переменные обладают свойством однородности и аддитивности, вид уравнений упрощается, что позволяет решать их аналитическими или численными (приближенными) методами. Благодаря простоте линейные модели широко применяются, хотя большинство процессов – нелинейно.

Линейность – свойство системы, которое позволяет делать выводы о поведении системы для всего класса входных воздействий, основываясь на том, как она реагирует лишь на некоторые из них. Общая реакция системы на входные воздействия является суммой отдельных реакций.

Основное свойство линейных систем – выполнение принципа суперпозиции решений: линейной комбинации произвольных входных сигналов ставится в соответствие та же линейная комбинация сигналов на выходе из системы: любая линейная комбинация решений также является решением задачи, т.е. если известны решения Y₁при Х₁ и Y ₂ при Х₂, то решение для выходных параметров при Х =Х₁ + Х₂ есть Y= Y₁ +Y₂.

Пусть на одном интервале t₀t заданы два фрагмента Х_t0t' и Х_t0t'' различных входных процессов Х_Т' и Х_Т'', а в момент времени t₀ - два различных состояния z' (t₀) и z'' (t₀). Введем в рассмотрение фрагменты Х_t0t = Х_t0t' + Х_t0t'' и кХ_t0t , а также состояния z (t₀) = z' (t₀) + z'' (t₀) и к z (t₀).

По отношению к операциям умножения и сложения операторы могут быть однородны и аддитивны.

Операторы α и β однородны, если

α (t₀t, к z (t₀), кХ_t0t) = к α (t₀t, z (t₀), Х_t0t);

β (t₀t, к z (t₀), кХ_t0t) = к β (t₀t, z (t₀), Х_t0t).

Операторы α и β аддитивны, если

α (t₀t, z (t₀), Х_t0t) = α (t₀t, z' (t₀), Х'_t0t) + α (t₀t, z'' (t₀), Х''_t0t);

β (t₀t, z (t₀), Х_t0t) = β (t₀t, z' (t₀), Х'_t0t) + β (t₀t, z'' (t₀), Х''_t0t).

Принцип суперпозиции предполагает

[x (t) = x₁ (t) + x₂ (t)] → [y (t) = y₁ (t) + y₂ (t)],

где x₁ (t) и x₂ (t) - некоторые входные воздействия, а y₁ (t) и y₂ (t) - выходные отклики на каждый из них в отдельности.

Конечное состояние системы определяется как сумма состояний, в которые перешла бы система под воздействием фрагментов входных воздействий.

Линейные системы дают возможность разложения величин z (t) и y (t) на составляющие, изучение которых можно проводить независимо друг от друга.

О качественных свойствах общего случая можно судить по свойствам частного – различие между решениями носит только количественный характер. Или: в случае линейных моделей отклик системы на изменение каких-либо условий пропорционален величине этого изменения.

Линейной моделью представляются простые объекты, она полезна в начале цепочки моделей, последовательно приближающихся к модели с требуемой адекватностью. Линейная модель часто позволяет сразу получить оценку порядка значений выходных переменных.

Нелинейная модель не подчиняется принципу суперпозиции, знание о поведении части системы еще не гарантирует знания поведения всей системы, а ее отклик на изменение каких-либо условий может качественно зависеть от величины этого изменения.

Нелинейность характеристик объекта означает невозможность разделения системы и исследования ее по частям. Действительно, для линейных систем справедлив принцип суперпозиции, т.е. если

R = kV, где V — воздействие, R — реакция, k — коэффициент пропорциональности, и

R₁ = kV₁ R₂ = kV₂, то для суммарного воздействия V₃ = V₁ + V₂ будет справедливо R₃ = k(V₁ + V₂) = kV₁ + kV₂ = R₁ + R₂, т.е. суммарная реакция R₃ будет равна сумме реакций на отдельные воздействия.

Если же реакция на воздействие нелинейна, например, R = kV²,

то принцип суперпозиции перестает выполняться и R₃ = k(V₁ + V₂)² ≠ kV₁ + kV₂

Таким образом, мы уже не можем заменить изучение реакции системы на сложное воздействие R₃ изучением ее реакций на более простые воздействия R₁ и R₂.

Иногда нелинейную задачу удается свести к последовательности линейных. Линеаризацией нелинейной задачи можно получить линейную модель для достаточно корректной оценки воздействия на систему малых возмущений.

То, что точно схватывает и передает характерные особенности одного класса нелинейных функций, ничего не говорит даже о простейших особенностях типичного представителя другого класса. Геометрический образ нелинейной функции — кривая на плоскости, искривленная поверхность. На одинаковые приращения независимой переменной одна и та же нелинейная функция откликается по-разному в зависимости от того, какому значению независимой переменной придается приращение.

Почти полным безразличием к изменению одних и повышенной чувствительностью к изменению других значений независимой переменной нелинейные функции резко отличается от линейных. Именно здесь и проходит демаркационная линия между миром нелинейных и миром линейных явлений.

В какой бы области естествознания ни возникала нелинейность явлений, она глубоко «функциональна». В физике нелинейность — это учет различного рода взаимодействий, обратных влияний и тонких эффектов, не учитываемых в линейной постановке. В химии нелинейность отражает обратные связи в скрытых механизмах реакций. В биологии нелинейность имеет эволюционный смысл: только сильная нелинейность позволяет биологическим системам охватить громадный диапазон жизненно значимых малых воздействий среды. Те, которые не сумели этого сделать - вымерли, не выдержав борьбы за существование. На их могилах можно было бы написать: «Они были слишком линейными для этого мира»

Вопрос о возможности и целесообразности перехода от нелинейности к линейности решается в каждой задаче конкретно на рациональном уровне.

Большинство реальных процессов нелинейны, а линейные их модели отвечают весьма частным случаям и, как правило, служат первым приближением к реальности.

Нелинейные уравнения можно разделить на два подкласса: алгебраические, в которых над переменными производятся только действия сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем, и трансцендентные, в которые входят другие функции от переменных (показательные, тригонометрические и др.). В любом случае сложность модели существенно зависит от числа уравнений и вида входящих в них функций. Обычно наиболее просто решаются алгебраические уравнения 1-й степени (линейные), наиболее сложно – трансцендентные.

Пример – закон Гука о линейной зависимости перемещения от растягивающей силы F = - кx. Упругость означает существование однозначной монотонно возрастающей функции, связывающей напряжение s = F/S (S - площадь поперечного сечения) и деформацию ε = x/l (x – относительное перемещение концов, l – длина образца): s = f (ε), f (0) = 0. Функция f в общем случае нелинейная. Нелинейными упругими свойствами обладают, например, высокоэластичные резиновые шнуры – ели такой шнур растянуть в десять раз (ε = 0,9), а затем отпустить, он восстановит свою длину. Если длинные металические проволоки подвергать малым деформациям (ε = 0,001), нелинейность не обнаруживается. При растяжении металлического стержня по мере возрастания растягивающего напряжения s деформация ε сначала растет по линейному закону. Это означает, что при таких ε первый член разложения функции s = f (ε) (полагая ее аналитической) в степенной ряд s = ε ∂f /∂ε +½! ε²∂²f /∂ε² + ... значительно превосходит все остальные. Тогда s = Еε (Е – модуль упругости материала при его одноосном сжатии). Нелинейный закон – параболическая зависимость

s = Аε - Вε².

Применение иерархического подхода позволяет на определенном этапе моделирования принимать упрощающие предположения, например, о линейности моделей.

Линейные модели занимают определенную нишу в исследованиях – любая линейная теория ограничена в определенных пространственных и временных рамках при малых интенсивностях воздействий на систему. Например, в строительстве не учитывают кривизну Земли, в космической технике не прибегают к теории относительности при несоизмеримых скоростях.

Методы исследования линейных систем очень развиты и обоснованное применение линейной модели для нелинейной системы часто оказывается весьма эффективным.

Если нелинейность является принципиальной, то применение линейных систем не дадут даже качественной картины процесса.

Например, закон тяготения изначально нелинейный (квадратичная зависимость силы взаимодействия между массами), и потому основанные на нем модели также нелинейны. Нелинейность может быть также обусловлена геометрией явления, изменением состояния (изменение жесткости пружины при исследовании колебательного процесса).

Источником нелинейности могут быть различные причины. Обычно принято считать, что при малых (не всегда) отклонениях системы от положения равновесия соотношения между перемещениями или скоростями ее элементов и возникающими силами линейны.

Например, силы трения между поверхностями (поверхности разделены смазочным материалом жидкостью или газом) линейно зависят от скорости перемещения поверхностей, с увеличением скорости эта зависимость становится нелинейной – вязкое трение зависит от квадрата скорости (турбулентное трение).

Обыкновенные дифференциальные модели

Одна из основных задач классической механики - задача прогнозирования движения различных тел и сред – решается на основе математической модели механического движения, которая представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта. С помощью дифференциальных моделей решается большинство задач механики, гидродинамики, электродинамики и др.

Дифференциальное уравнение – уравнение, содержащее неизвестную функцию одного или нескольких переменных, независимые переменные и производные неизвестной функции по независимым переменным.

Обыкновенное дифференциальное уравнение – уравнение, в котором неизвестной является функция от одного независимого переменного, причем, в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков:

F[x, y(x), y’(x), …, y⁽ⁿ⁾(x)] = 0.

Общее решение: y = y(x, C₁,…, C_n), при любом наборе С – частное решение.

Задача Коши (задача с начальными условиями) – задача о нахождении частного решения, которое удовлетворяет n частным условиям y(x₀) = y₀, y’(x₀) = y’₀,…, y^(n-1)(x₀) = y^(n-1) ₀.

Система обыкновенных дифференциальных уравнений для r неизвестных функций имеет вид

F_i[x, y₁, y₂, …,y_r, y’₁, y’₂,…, y’_r,…, yⁿ₁, yⁿ₂, …, yⁿ_r] = 0 , i = 1,…, r.

Линейное обыкновенное дифференциальное уравнение – линейно относительно искомой функции, независимого переменного и ее производной, т.е. уравнение вида

y⁽ⁿ⁾ + a₁(x)y^(n-1) + … + a_n-1(x)y¹ + a_n(x)y = f(x),

y(x) – искомая функция, a_i(x), f(x) – заданные функции.

Задача прогнозирования движения (задача математического анализа) решается интегрированием дифференциальных уравнений движения при заданных начальных условиях (задача Коши) - пассивный расчет траектории движения объекта. Усложнение задачи – определить, какими должны быть начальные скорости объекта, чтобы из одного заданного положения он переместился в другое заданное – здесь уже присутствует элемент управления движением. Дальнейшее усложнение – траектория движения из одного положения в другое должна обладать определенным экстремальным свойством, например, минимальное время движения (задача о брахистохроне).

Законы механики – описание движения системы точек или твердого тела могут быть сведены к задаче нахождения решений ОДУ. Анализ устойчивости движения, химические реакции, теория колебаний, теория оптимального управления представляют собой динамические системы и могут быть формализованы ОДУ.

Процесс составления дифференциального уравнения по условию задачи (физической, технической) состоит в выражении на математическом языке связи между переменными величинами и их бесконечно малыми приращениями.

Построение обыкновенных дифференциальных моделей зависит от законов в конкретной предметной области.

Большинство дифференциальных уравнений не может быть проинтегрировано в замкнутой форме (даже если известно, что такое решение имеется), т.е. не удается представить решение в виде аналитической зависимости, использующей конечное число операций над элементарными функциями (решение в виде бесконечного ряда далеко не всегда позволяет исследовать необходимые свойства).

Приемы и методы, которые позволили бы, не решая самих дифференциальных уравнений, получать необходимые сведения о тех или иных свойствах решений, предоставляет качественная теория дифференциальных уравнений.

В основе этой теории лежат общие теоремы о существовании и единственности решений, о непрерывной зависимости решений от начальных параметров. Численному интегрированию дифференциальных уравнений обязательно должно предшествовать обращение к теоремам существования и единственности.

4.3 Классификация математических моделей в зависимости от параметров модели

Непрерывные и дискретные модели

Процесс функционирования системы может протекать непрерывно или дискретно. Решение о дискретности или непрерывности модели принимается на этапе постановки задачи также на рациональном уровне.

Непрерывная система функционирует в непрерывном времени (интервал ее функционирования T = [t₀, t_k] представляет собой отрезок оси действительных чисел, заданный началом t₀ и концом t_k), непрерывно изменяется состояние системы (непрерывны операторы α и β). Малые изменения входных воздействий приводят к такого же порядка малым изменениям состояния системы и выходных воздействий.

Модель непрерывная, если она описывает поведение системы для всех моментов времени из некоторого промежутка.

Модель S = gt²/2, 0 < t < 100 непрерывна на промежутке времени (0; 100).

Непрерывные модели применяются при изучении систем, связанных с непрерывными процессами, которые описываются с помощью систем дифференциальных уравнений, задающих скорость изменения переменных системы во времени. Непрерывные модели можно описать с помощью конечно-разностных уравнений, которые в пределе переходят в соответствующие дифференциальные уравнения.

Дискретная система функционирует в дискретном временном пространстве и определяется дискретными состояниями - изменения ее состояния происходят лишь в дискретные моменты времени (дискретный интервал функционирования).

Дискретными могут быть системы, для которых дискретным является или только время, или только состояния. Это широкий и практически важный класс систем – в него входят все дискретные (цифровые, измерительные, управляющие и вычислительные, в том числе ЭВМ) устройства.

Дискретность временного пространства означает, что явления, сопровождающие изменения состояния системы, могут происходить лишь в моменты времени, образующие некоторое дискретное множество, в котором моменты времени можно пронумеровать. В частности, переходы системы из одного состояния в другое могут осуществляться в целочисленные моменты времени. Общий случай сводится к этому частному введением целочисленной нумерации моментов возможных изменений состояний.

Если рассматривать только t - 0, 1, 2, ..., 10 (с), то модель S₁ = gt²/2, или числовая последовательность S₀ = 0, S = g/2, S₂ = 2g, S₃ = 9g/2, ..., S₁₀= 50g, может служить дискретной моделью движения свободно падающего тела.

Непрерывная система может рассматриваться как дискретная. Это достигается путем учета ее состояния лишь в отдельные моменты времени и округления их значений до целых единиц.

Системы с дискретными состояниями характеризуются тем, что в любой момент времени можно однозначно определить, в каком именно состоянии находится система. Для такой идентификации обязательно нужно знать тот признак, который отличает одно состояние системы от другого. Например, при исследовании систем массового обслуживания в качестве такого признака обычно используют число заявок в системе. Соответственно, изменение числа заявок в системе интерпретируется как переход системы в новое состояние.

Если же не удается подобрать такой признак, либо его текущее значение невозможно зафиксировать, то систему относят к классу систем с непрерывным множеством состояний.

Смена состояний может происходить либо в фиксированные моменты времени, множество которых дискретно (например, поступление новых заявок на обслуживание), либо непрерывно (изменение температуры тела при нагревании). В соответствии с этим различают системы с дискретным временем переходов (смены состояний) и системы с непрерывным временем переходов (точнее, «живущие» в непрерывном времени).

Дискретными могут быть системы с дискретным вмешательством случая – эти системы почти всегда ведут себя как непрерывные и только в дискретные моменты времени испытывают случайные воздействия. По условиям перехода из одного состояния в другое системы могут быть детерминированными или стохастическими.

Изучением свойств непрерывного характера занимается классическая математика. В дискретной математике отказываются от основополагающих понятий классической математики – предела и непрерывности.

Использование классической или дискретной математики зависит от задач исследований – какая модель явления рассматривается – дискретная или непрерывная. Основные разделы дискретной математики: математическая логика, вычислительная математика (численное интегрирование), теория графов (задачи анализа структур, экономические задачи, электротехнические задачи – трассировка), теория кодирования (хранение, обработка, передача информации), теория функциональных систем (описание функционирования сложных систем по функционированию их компонент, правила построения сложных управляющих систем).

Детерминированные и неопределенные модели

Закономерности, описывающие процессы и явления объективного мира, можно условно разделить на две группы: однозначно определенные (детерминированные) и находящиеся в условиях неопределенности.

В зависимости от способа задания параметров, исходной информации, начальных условий и способа нахождения характеристик системы, математические модели можно подразделить на два больших класса: детерминированные и неопределенные (вероятностные, стохастические).

В детерминированных моделях все исходные данные, ограничения и целевая функция (т.е. некоторое соотношение, количественно характеризующее поставленную перед системой цель) задаются в виде конкретных чисел, векторов или числовых функций.

В детерминированных моделях используются различные классические методы математики: дифференциальные, линейные, разностные и интегральные уравнения, операторы для сведения к алгебраическим моделям и др. При совместном рассмотрении этих соотношений состояния системы в заданный момент времени однозначно определяются через параметры системы, входную информацию и начальные условия.

По степени математической абстракции детерминированные модели можно разделить на сложные и упрощенные.

Сложные модели описывают все причинные связи какой-то реальной системы и позволяют точно прогнозировать поведение системы в зависимости от изменения переменных (или параметров).

Упрощенные модели описывают только существенные зависимости (идеализированные модели).

Между этими двумя моделями существует ряд моделей, отличающихся степенью детализации. На практике чаще всего применяются упрощенные модели с разной степенью детализации. При этом считается, что имеются существенные и несущественные факторы: существенные учитываются, несущественные отбрасываются. Между принятыми в модели факторами и результирующими показателями устанавливается жесткая детерминированная связь. Широкое распространение идеализированных моделей вызвано их простотой и возможностью логического обоснования.

Детерминированные системы – системы, процессы в которых взаимосвязаны так, можно проследить цепь причин и следствий.

К детерминированным относятся те закономерности, которые по заданным с определенной точностью характеристикам входных воздействий позволяют установить вполне определенный (детерминированный) отклик (реакцию) выходных воздействий исследуемого объекта.

В статическом режиме детерминированные системы описываются алгебраическими уравнениями, в динамическом режиме – дифференциальными уравнениями.

Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае модель недетерминированная, стохастическая (вероятностная).

Приведенные выше физические модели — детерминированные. Если в модели S(p) = g(p)t2/2, 0 < t < 100 мы учли бы случайный параметр — порыв ветра с силой р при падении тела, например, так: S = gt2/2, 0 < t < 100, то мы получили бы стохастическую модель (уже не свободного) падения.

При решении одних задач случайные составляющие практически не влияют на результат и в модели не учитываются. В других задачах решение может быть получено только при учете случайных составляющих или различных неопределенностей, и соответствующие математические методы закладываются в модель.

Достаточность детерминированной модели или необходимость учета неопределенностей иногда очевидна, иногда переход к модели, учитывающей неопределенность, происходит вследствие неудовлетворенности результатами, полученными на детерминированной модели.

Неопределенность понимается в том смысле, что соответствующие характеристики системы находятся в условиях приближения и неполноты информации. В «чистом виде» неопределенных процессов нет - описание неопределенности может быть разным в зависимости от количества и качества имеющейся информации (имеется не вся необходимая информация, элементы могут быть описаны по аналогам, что не всегда соответствует целям исследований). Характеристики системы зависят от большого количества различных факторов (некоторые из них могут быть вообще неизвестны), выбор для моделирования существенных факторов, влияющие на систему, может иметь неоднозначный характер (как объективный, так и субъективный).

В зависимости от типа неопределенности – методы описания неопределенных данных, включая вероятностную, нечеткую и интервальную модели, - каждая из них имеет свои методы анализа и область применения.

Математически неопределенность может быть описана стохастически, статистически, с позиций нечетких множеств.

Стохастическое описание используется тогда, когда неопределенные параметры носят вероятностный (случайный) характер. При этом необходимо, чтобы был определен закон распределения таких случайных параметров.

В стохастической системесостояние и выход – случайные величины, операторы перехода и выхода не определяют конкретные значения состояния и выхода, как в детерминированном случае, а лишь устанавливают вероятности их реализации.

Статистическое описание является частным случаем стохастического – заданы только выборочные оценки каких-либо характеристик случайной величины или наборы некоторых случайных параметров.

Нечеткая модель основана на понятии нечеткого множества (нечеткая переменная и ее функция принадлежности, задающая степень принадлежности конкретного значения величины х некоторому множеству s).

При описании с позиций нечетких множеств неопределенный параметр задается некоторым множеством возможных его значений, определяющих степень принадлежности объекту (например, при выделении элементов из внешней среды). Нечеткое множество описывает систему с нечеткими, размытыми границами. Обычно функция принадлежности задается экспертным путем на основе информации об источниках неопределенности переменной х.

Интервальная модель – неопределенность параметра х описывается его возможными значениями в виде [x] = [x_min; x_max]. Внутри интервала не задается никакой вероятностной меры – все значения внутр интервала предполагаются равновозможными (не путать с равновероятными).

Любому реальному процессу присущи случайные флюктуации (отклонения от средних значений). Однако выбор детерминированной или вероятностной математической модели зависит от того, учитываются ли случайные факторы. Выделение детерминированных моделей в отдельный класс объясняется широким их применением и разнообразием математических методов решения детерминированных задач.

Если хотя бы один параметр модели или ограничительная функция имеет в качестве своих значений случайный вектор или случайную величину, то это случайная (стохастическая) модель. В этом случае под однозначностью определения характеристик моделируемого процесса понимается однозначное определение распределений вероятностей для характеристик процесса при заданных распределениях вероятностей для начальных условий и возмущений.

Стохастический характер модели связан с наличием в объекте и среде различных неконтролируемых, но существенных факторов, которые можно моделировать статистически. Состояние системы в этом случае Y=F(X, U, E(t)), где E(t) – случайный процесс, моделирующий имеющуюся неопределенность объекта и среды. Эта неопределенность может быть связана как с быстрым изменением параметров объекта, так и с помехами, накладывающимися на измеряемые значения сигналов на входе и выходе объекта.

Стохастический объект и его модель ведут себя неоднозначно в одинаковых ситуациях, что моделируется случайным вектором E(t), статистические свойства которого должны быть заданы. В простейшем случае Y=F(X, U)+E(t).

Примером стохастического объекта является любой биологический организм, который в одинаковых условиях ведет себя по-разному. В этом случае Y описывает поведение объекта, которое строго зависит от внешних условий, а все отклонения от этого регулярного поведения образуют «случайную помеху» E(i).

Переход от детерминированной модели к стохастической осуществляется таким образом, чтобы она отражала в себе случайный характер данных и самой модели. Способ перехода выбирается в зависимости от сведений об изучаемой модели: уверенности в правильности и надежности данных и модели. При этом возможно, что эти сведения ошибочны.

В общем случае для стохастических объектов оператор является случайным (например коэффициенты линейного дифференциального уравнения, весовые функции и т.д.).

В зависимости от учета в модели случайностей при работе и управлении объектом моделирования непрерывности или дискретности процесса рассматривают дискретно-детерминированные, дискретно-детерминированные, непрервно-детерминированные, дискретно-стохастические, непрерывно-стохастические модели.

Статические и динамические модели

Существенным признаком классификации моделей является их возможность описывать изменения параметров объекта во времени.

Статичный или динамичный характер системы (что отображается в модели) определяется в зависимости от целей моделирования. При построении модели основным является сравнение времени существенных изменений внешних воздействий и соответствующих характерных временных переходов объекта в новое равновесное состояние с окружающей средой и между элементами внутри системы.

В статической модели можно выделить важнейшие свойства и параметры (или сочетания), определяющие качество системы, не зависящие от времени (надежность, стоимость, долговечность и др.). В статической модели объект сохраняет состояние равновесия: параметры остаются постоянными при постоянных внешних воздействиях.

Модель называется статической, если среди параметров, участвующих в описании модели, нет временного параметра. Статическая модель в каждый момент времени дает лишь «фотографию» системы, ее срез.

Закон Ньютона F = ma — это статическая модель движущейся с ускорением а материальной точки массой т. Эта модель не учитывает изменение ускорения от одной точки к другой.

При таком подходе можно ставить оптимизационные задачи по критерию, выраженному этой функцией. В случае линейной целевой функции, линейных неравенств, линейной математической модели задачи технико-экономического содержания (например, распределение ресурсов) решаются как задачи линейного программирования.

Если изменения параметров во времени происходят столь медленно, что ними можно пренебречь, то такую модель называют квазистатической.

Модель динамическая, если среди параметров модели есть временной параметр, т. е. она отображает систему (процессы в системе) во времени.

В динамической модели от времени зависят независимые переменные (параметр процесса), неизвестные функции (фазовые переменные), характеризующие состояние системы (перемещения, скорости, ускорения элементов системы, силы и моменты, давление и расход жидкости в трубопроводе, напряжение и сила тока в электрической сети и др.).

Модель S = gt^z/2 — динамическая модель пути при свободном падении тела. Динамическая модель типа закона Ньютона: F(t) = a(t)m(t). Еще лучшей формой динамической модели Ньютона является: F(t) = s"(t)m(t).

Динамические системы могут быть с дискретными состояниями (множество состояний конечно или счетно) или с непрерывным множеством состояний.

В детерминированных системах новое состояние зависит только от времени и текущего состояния системы. Если имеются условия, определяющие переход системы в новое состояние, то для детерминированной системы можно однозначно указать, в какое именно состояние она перейдет.

Для стохастической системы можно указать лишь множество возможных состояний перехода и, в некоторых случаях, - вероятностные характеристики перехода в каждое из этих состояний.

Основная форма динамической математической модели - дифференциальные уравнения.

Стационарные и нестационарные модели

Стационарные системы – такие системы, свойства которых не изменяются во времени.

Реакция стационарной системы на любой заданный тип возмущения зависит только от интервала времени между моментом начала действия входного возмущения и данным моментом времени, т.е. свойство стационарности означает, что процесс преобразования входных сигналов инвариантен относительно сдвига, как от текущего времени, так и от момента приложения входного сигнала. Реакция нестационарной системы зависит как от текущего времени, так и от момента приложения входного сигнала. В этом случае при сдвиге входного сигнала во времени (без изменения его формы) выходные сигналы не только сдвигаются во времени, но и изменяют свою форму.

Примеры стационарных моделей.

При ламинарном течении жидкости (скорость течения невелика) в длинной трубе постоянного сечения на достаточно большом удалении от входа частицы жидкости движутся параллельно оси трубы, и профиль скоростей частиц в сечении остается с течением времени неизменным – параметры модели не зависят от времени.

Термодинамическое равновесие обшивки самолета при полете в плотных слоях атмосферы. Обшивка, получая тепловую энергию от воздушного потока, одновременно излучает ее в окружающее пространство, в соответствии с законом Стефана-Больцмана тем больше, чем выше ее температура (ε_Т = σ Т⁴, ε_Т – интегральная излучательная способность – энергия излучения с единицы поверхности в единицу времени, σ – постоянная).

В общем случае состояние системы z (t) и выход системы y (t) являются функциями не только z (t₀), и Х_t0t, но и самого интервала t₀t:

z (t) = α (t₀t, z (t₀), Х_t0t); у (t) = β (t₀t, z (t₀), Х_t0t).

При одних и тех же значениях z (t₀), и Х_t0t, перемещая по оси времени интервал t₀t, можно получить различные значения z (t) и y (t).

Введем в рассмотрение оператор сдвига Ñ^t, применение которого к произвольной величине приводит к ее сдвигу вдоль оси времени на интервал t.

Система называется стационарной, если для операторов перехода и выхода выполняются условия:

z (Ñ^tt) = α (Ñ^t t₀t, Ñ^t z (t₀), Ñ^t Х_t0t) = Ñ^t z (t);

у (Ñ^tt) = β (Ñ^t t₀t, Ñ^t z (t₀), Ñ^t Х_t0t) = Ñ^t у (t).

На рисунке 3.1 представлено второе из условий, согласно которому должно выполняться равенство у (Ñ^tt) = Ñ^t у (t).

Для стационарной системы модель функционирования можно записать в виде, независимом от t₀t:

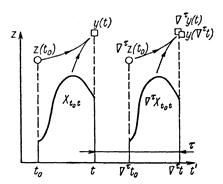z (t) = α (z (t₀), Х_t0t); у (t) = β (z (t₀), Х_t0t).

Стационарные модели применяются для описания различных потоков (жидкости, газа, тепла) в случае постоянства условий на входе и выходе потока.

В нестационарной модели время – одно из существенных переменных. Например, движение жидкости в трубе при изменении параметров на входе (изменение скорости при истечении жидкости из сосуда).

Стационарные математические модели описывают системы, в которых протекают так называемые установившиеся процессы – процессы, в которых интересующие нас параметры постоянны во времени.

К установившимся (стационарным) относят и периодические процессы, в которых некоторые выходные параметры остаются неизменными.

Например, математическая модель маятника является стационарной по отношению к независящим от времени периоду и полуразмаху колебаний, хотя материальная точка перемещается во времени относительно положения равновесия.

Частным случаем стационарных моделей являются модели статические, которые включают описание связей между основными переменными процесса в установившихся режимах (в равновесном состоянии без изменения во времени).

Например, математическое описание статики химико-технологического процесса состоит обычно из трех видов уравнений: материального и теплового балансов, термодинамического равновесия системы (характеристика движущей силы) и скоростей протекания процессов (химических реакций, тепло- и массопередачи и т.п.).

Для расчетов медленных процессов или процессов, протекающих с небольшими отклонениями от стабильных условий, принимается допущение, позволяющее считать процесс установившимся.

Подобное допущение принимается, например, для расчета теплового баланса турбины при половинной, трехчетвертной или полной нагрузке или для решения методами линейного программирования задачи смешения материалов.

Стационарные математические модели (кроме статических) обычно состоят из дифференциальных уравнений, статические – из уравнений алгебраических.

Дата добавления: 2014-08-04; просмотров: 599; Нарушение авторских прав

Мы поможем в написании ваших работ!