
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сравнение средних
Вряд ли можно встретить исследования в сфере управления, где бы не потребовалось обнаружить и доказать изменение или, напротив, стабильность значения какой-либо переменной под влиянием тех или иных факторов. Однако далеко не всегда можно увидеть оценку статистической значимости этого изменения или стабильности. В то же время выполнить такой анализс помощью любой статистической программы, как правило, содержащей процедуру “анализ средних” не представляет никаких затруднений.
Ниже после краткого теоретического введения будет приведен ряд примеров, которые покажут практическую важность статистической оценки различия средних.
Гипотезы, построенные на основе анализа средних, проверяются на различном уровне обоснованности, начиная с простого сопоставления и заканчивая детальной проверкой статистической значимости различий. Основой сравнения средних является понятие доверительного интервала для разности средних, который при статистически значимом их различии не должен включать в себя нуль.
В первом приближении это означает, что доверительные интервалы для сравниваемых средних не должны перекрываться. А поскольку программы статистического анализа позволяют находить доверительные интервалы и строить ящичковые диаграммы Тьюки, то уже по ним можно визуально приближенно оценить уровень значимости различия средних. Так, из ящичковых диаграмм, представляющих распределение численности занятых в экономике по однородной выборке регионов Центрального федерального округа (без г. Москвы, Московской и Воронежской областей) в 2000 и 2008 гг. (рис. 1.4), хорошо видно, что хотя медианы распределений этого показателя заметно различаются, это отличие не выходит за пределы междуквартильного разброса («ящичка»).
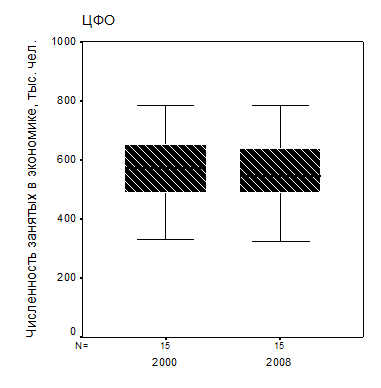
|
| Рис. 1.4. Распределение численности занятых в экономике по однородной выборке регионов Центрального федерального округа (без г. Москвы, Московской и Воронежской областей) в 2000 и 2008 гг. |
При более строгом подходе к сравнению средних необходимо различать по крайней мере три типовых случая. Проверяются следующие статистические гипотезы:
1. Различаются ли средние некоторой переменной, вычисленные в разных подгруппах наблюдений (t-критерий для независимых выборок);
2. Различаются ли средние двух переменных, вычисленные для одной группы наблюдений (t-критерий для парных выборок);
3. Отличается ли среднее отдельной переменной от некоторой заданной величины (одновыборочный t-критерий).
Из теории статистики известно, что любая статистическая гипотеза есть утверждение или предположение о параметрах генеральной совокупности. Обычно вначале выдвигают нулевую гипотезу (отсутствие различий, эффекта и т.п.) с тем, чтобы попытаться ее отвергнуть с учетом имеющейся информации (достаточно общий подход; примерно то же мы наблюдаем, например, в юриспруденции, где принята так называемая “презумпция невиновности”). При решении первой задачи (различаются ли средние некоторой переменной, вычисленные в двух подгруппах наблюдений) нулевая гипотеза формулируется так:
H0: m1 = m2, (1.1)
где m1 и m2 – генеральные средние двух подвыборок, т.е. два выборочных средних получены из совокупностей с одинаковыми средними. Предполагается, что переменная имеет нормальное распределение, причем не обязательно с равными дисперсиями в подвыборках. Рассчитывается t-критерий, равный отношению разности средних к оценке ее стандартной ошибки (напомним, что стандартная ошибка среднего равна среднеквадратическому отклонению, иначе называемому стандартным отклонением, деленному на квадратный корень из объема выборки:
s[ 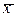 ] = s/
] = s/ 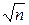 ).
).
Формулы несколько отличаются в зависимости от того, объединяются или нет дисперсии подвыборок:
при объединении дисперсий, т.е. в случае их равенства (в статистическом смысле)
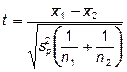 , (1.2)
, (1.2)
где объединенная дисперсия
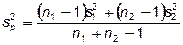 ; (1.3)
; (1.3)
при “раздельных” дисперсиях (равенства дисперсий не предполагается)
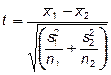 , (1.4)
, (1.4)
Здесь 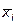 – среднее группы i;
– среднее группы i; 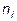 – число наблюдений в группе i;
– число наблюдений в группе i; 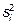 – выборочная дисперсия в группе i. Формулы (1.2)-(1.4) – для двустороннего критерия; чтобы получить вероятности одностороннего критерия, следует полученное значение р-уровня разделить на 2.
– выборочная дисперсия в группе i. Формулы (1.2)-(1.4) – для двустороннего критерия; чтобы получить вероятности одностороннего критерия, следует полученное значение р-уровня разделить на 2.
В качестве примера применения t-критерия для независимых выборок сравним средние для переменной “Уровень экономической активности мужского населения в 2009 г., %” для регионов Центрального Нечерноземья (ЦР) и Центрального Черноземья (ЦЧ) – см. табл. 1.1.
Таблица 1.1
Групповые статистики переменной “Уровень экономической активности мужского населения в 2009 г., %”
| Код | N | Среднее | Стд. отклонение | Стд. ошибка среднего | |
| Уровень экономической активности мужчин в 2009 г., % | ЦР | 72,808 | 2,8366 | 0,8189 | |
| ЦЧ | 70,640 | 1,5076 | 0,6742 |
Из данных табл. 1.1 следует, что средние по регионам ЦР и ЦЧ заметно отличаются: при m1=78,808 и m2=70,640 их разность составляет m1-m2=2,168. Сумма стандартных ошибок средних равна 0,8189+0,6742=1,4934, что меньше разности средних, однако эту величину следует увеличить примерно вдвое, чтобы выйти на уровень статистической значимости 5% (коэффициент доверия составляет величину около 2 для доверительной вероятности 0,95), что составит 2´1,4934=2,9862. Разность средних находится между этими двумя значениями, следовательно, можно рассчитывать на статистическую значимость различий этих двух экономико-географических районов по анализируемой переменной “Уровень экономической активности мужского населения” на уровне надежности меньше 95%, но больше 67% (этой величине соответствует коэффициент доверия 1). Точного решения мы в данном случае дать не можем, это лишь грубая “прикидка”. Точный расчет дает обращение к процедуре “Compare Means” программы SPSS Base (табл. 1.2): величина t-критерия для независимых выборок значима на уровне 0,021 в предположении равенства дисперсий и на уровне 0,103 в предположении их неравенства.
Таблица 1.2
Групповые статистики переменной “Уровень экономической активности мужского населения в 2009 г., %”
| Критерий равенства дисперсий Ливиня | t-критерий равенства средних | ||||||||
| F | Знч. | t | Ст. св. | Знч. (2-сторон) | Средняя разность | Стд. ошибка разности | 95% доверительный интервал разности | ||
| нижняя граница | верхняя граница | ||||||||
| Предпола-гается равенство дисперсий | 7,204 | 0,017 | 1,597 | 0,131 | 2,168 | 1,3578 | -0,7257 | 5,0624 | |
| Равенство дисперсий не предпо-лагается | 2,044 | 13,680 | 0,061 | 2,168 | 1,0607 | -0,1117 | 4,4484 |
Остается нерешенным – какое из предположений справедливо? Ответ на этот вопрос дает обращение к критерию равенства дисперсий Ливиня. Он применяется для того, чтобы определить, различается ли разброс переменной в сравниваемых подвыборках. Нулевая гипотеза в данном случае следующая: дисперсии двух совокупностей равны. Если вычисленный уровень значимости меньше 0,05 или даже 0,01, то для средних следует использовать t-критерий с раздельными дисперсиями.
Поскольку при величине статистики F=7,204 критерий Ливиня показывает значимость 0,017 (табл. 1.2), гипотезу о равенстве дисперсий следует отвергнуть. В этом случае мы должны принять следующее решение: различие средних значимо лишь на уровне 0,061. Это означает, что надежность вывода о том, что уровень экономической активности мужского населения в регионах Центральной России в среднем больше по сравнению с аналогичным показателем в регионах Центрального Черноземья, составляет менее 94%, и эту гипотезу следует отклонить.
Аналогичный вывод можно сделать, оценив стандартную ошибку разности средних. Согласно табл. 1.2, эта величина равна 1,0607, а 95%-й интервал составляет (-0,1117; 4,4484) и включает в себя нуль. Отсюда заключаем, что разность средних на традиционно принимаемом уровне значимости 0,05 не является статистически значимой.
Часто исследователь сталкивается несколько с иной ситуацией, когда на одной и той же выборке наблюдается две переменные, измеряющие один и тот же признак, но относящиеся, например, к разным моментам времени. В этих случаях для сравнения средних используется t-критерий для парных выборок. Пары наблюдаемых значений могут возникать по крайней мере тремя способами. Во-первых, можно делать два измерения у одного статистического объекта (сравниваются средние для двух переменных). Во-вторых, можно измерять одну и ту же переменную дважды – до и после какого либо воздействия. В-третьих, можно измерять одну и ту же случайную величину (признак) в парной выборке, т.е. у пар статистических объектов, выбранных из-за их сходства по отношению к цели измерений, благодаря чему достигается возможность контроля над внешними факторами.
Теория статистических выводов здесь проста: поскольку выборка одна и известны сравниваемые пары, то вычисляются разности di для каждой статистической единицы (наблюдения), а затем к этой случайной величине применяют обычный t-критерий для обнаружения значимости отличия среднего значения 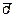 от нуля. Расчетная формула для t-критерия может быть представлена так:
от нуля. Расчетная формула для t-критерия может быть представлена так:
t = 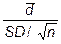 , (1.5)
, (1.5)
где SD – стандартное отклонение разностей; n – объем выборки.
Приведем пример анализа средних в парных выборках, продолжив предыдущий анализ уровень экономической активности населения в регионах ЦФО. Уровень экономической активности населения является “фоном” для многих социальных явлений, и в этой связи представляет интерес сравнить его значение в 2009 г. со значениями в предшествующий период.
В табл. 1.3, полученной с помощью процедуры “Compare Means” программы SPSS Base, представлены статистики парных выборок для двух переменных – “Уровень экономической активности населения в регионах ЦФОв 2009 г., %” и “Уровень экономической активности населения в регионах ЦФОв 2000 г., %” В выборку включены все регионы ЦФО, включая г. Москву.
Таблица 1.3
Статистики парных выборок переменных “Уровень экономической активности населения в регионах ЦФОв 2009 г., %” и “Уровень экономической активности населения в регионах ЦФОв 2000 г., %”
| Среднее | N | Стд. отклонение | Стд. ошибка среднего | ||
| Пара 1 | Уровень экономической активности населения в регионах ЦФОв 2000 г. | 64,961 | 2,2791 | 0,5372 | |
| Уровень экономической активности населения в регионах ЦФОв 2009 г. | 66,972 | 2,9233 | 0,6890 |
Если исходные данные рассматривать как независимые выборки, тогда различие средних 64,961-66,972=-2,011 будет, скорее всего, статистически незначимым, поскольку удвоенная сумма стандартных ошибок средних, составляющая 2´(0,5372+0,6890)=2,4524, больше разности средних. Однако зависимость выборок усиливает значимость различия средних. Действительно, из табл. 1.4 “Критерий парных выборок” видно, что значимость парной разности гораздо выше – менее 0,0005. (Обратим внимание на то, что и здесь доверительный интервал разности не включает в себя нуль.)
Таблица 1.4
Критерий парных выборок (переменные “Уровень экономической активности населения в регионах ЦФОв 2000 и 2009 гг., %”)
| Парные разности | t | Ст. св. | Знч. (2-сторон) | |||||
| Среднее | Стд. отклоне-ние | Стд. ошибка среднего | 95% доверительный интервал разности | |||||
| нижняя граница | верхняя граница | |||||||
| Уровень экономической активности населения в ЦФО в 2000 и 2009 гг. | -2,011 | 1,9596 | 0,4619 | -2,986 | -1,037 | -4,354 | 0,000 |
Заметим, что критерий парных выборок значительно чувствительнее t-критерия для независимых выборок. Это и понятно, поскольку при вычислении критерия парных выборок использована дополнительная информация. При этом чем больше корреляция между переменными (в рассматриваемом случае коэффициент линейной корреляции R=0,743), тем эффективнее парные выборки по сравнении с независимыми. Вывод информации о силе этой связи предусмотрен процедурой “Compare Means” программы SPSS Base (см. табл. 1.5).
Таблица 1.5
Корреляции парных выборок (переменные “Уровень экономической активности населения ЦФОв 2000 и 2009 гг., %”)
| N | Корреляция | Знч. | ||
| Пара 1 | Уровень экономической активности населения ЦФОв 2000 и 2009 гг. | 0,743 | 0,000 |
Как следует из табл. 1.5, выборочный коэффициент корреляции, равный 0,743, значим на уровне не хуже 0,0005, отвечает сильной связи рассматриваемых показателей по регионам ЦФО. Отчасти поэтому столь существенной оказалась статистическая значимость различия средних. В содержательном плане этот результат может быть проинтерпретирован как заметный рост экономической активности населения в регионах ЦФОв 2009 г. по отношению к уровню 2000 года.
Третий типовой случай – одновыборочный t-критерий – отвечает на вопрос: отличается ли среднее отдельной переменной от некоторой заданной величины? В теоретическом плане это самый простой вариант статистического вывода. Формулируется нулевая гипотеза:
H0: m - а = 0, (1.6)
где а – некоторое заданное значение измеряемой случайной величины. Эта разность играет роль величины 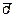 в формуле (1.5) для парного t-критерия. Для расчета t-критерия используется формула вида (1.5), где вместо SD (стандартного отклонения разностей) фигурирует sx – выборочное стандартное отклонение переменной:
в формуле (1.5) для парного t-критерия. Для расчета t-критерия используется формула вида (1.5), где вместо SD (стандартного отклонения разностей) фигурирует sx – выборочное стандартное отклонение переменной:
t = 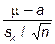 . (1.7)
. (1.7)
В формуле (1.7) n – объем выборки.
Продолжим рассмотренный ранее пример для иллюстрации этого типа сравнения средних. Уровень экономической активности населения в 2009 году в среднем по России составил 67,8% (так называемое “тестовое значение”). Сравним с этим тестовым значением аналогичный показатель по ЦФО. Как и ранее, воспользуемся процедурой “Compare Means” программы SPSS Base.
В табл. 1.6 приведены одновыборочные статистики переменной “Уровень экономической активности населения в регионах ЦФОв 2009 г.”, а в табл. 1.7 – одновыборочный критерий для этой переменной.
Таблица 1.6
Одновыборочные статистики переменной “Уровень экономической активности населения в регионах ЦФОв 2009 г., %”
| N | Среднее | Стд. отклонение | Стд. ошибка среднего | |
| Уровень экономической активности населения в регионах ЦФОв 2009 г., % | 66,972 | 2,9233 | 0,6890 |
Как следует из табл. 1.6 и 1.7, средняя величина анализируемого показателя меньше российского “стандарта”, но ненамного, всего на 0,8% (67,0 против 67,8%). Этого различия недостаточно, чтобы отвергнуть нулевую гипотезу о равенстве уровня экономической активности населения в 2009 г. в среднем по стране и по регионам ЦФО. Этот вывод подтверждает и очевидный факт включению нуля в 95%-й доверительный интервал (-2,281; 0,626) для средней разности между значениями переменной и “тестового значения”.
Таблица 1.7
Одновыборочный критерий для переменной “Уровень экономической активности населения в регионах ЦФОв 2009 г., %”
| Тестовое значение = 67,8 | ||||||
| t | Ст. св. | Знч. (2-сторон) | Средняя разность | 95% доверительный интервал разности | ||
| нижняя граница | верхняя граница | |||||
| Уровень экономической активности населения в регионах ЦФОв 2009 г., % | -0,201 | 0,246 | -0,828 | -2,281 | 0,626 |
В заключение рассмотрим проблему сравнения средних двух подвыборок не по одной, а одновременно по нескольким переменным. В этом случае используются те же приемы, но при расчете уровня статистической значимости необходимо провести корректировку Бонферрони, т.е. умножить вероятность каждого критерия на общее число сравнений. Корректировку следует проводить до того, как будет вычислен доверительный интервал, т.е., задавая уровень значимости a, следует разделить его значение на число сравнений. Так, если принимается “стандартное” значение a=0,05 и число сравнений 5, то при вычислении доверительных интервалов задается уровень 0,05/5=0,01, т.е. не 95%-й, а 99%-й интервал.
| <== предыдущая страница | | | следующая страница ==> |
| Предметный указатель | | | ПОВЫШЕНИЕ ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА – ОБЪЕКТИВНЫЙ ЭКОНОМИЧЕСКИЙ ЗАКОН ОБЩЕСТВЕННОГО РАЗВИТИЯ |
Дата добавления: 0000-00-00; просмотров: 627; Нарушение авторских прав

Мы поможем в написании ваших работ!