Однокомпонентные гетерогенные системы. Уравнение Клапейрона - Клаузиуса

Однокомпонентная гетерогенная система состоит из индивидуального вещества, которое может существовать в различных агрегатных состояниях или полиморфных модификациях.

Рассмотрим равновесный процесс перехода вещества из фазы 1 в фазу 2. В условиях равновесия молярная энергия Гиббса вещества в первой и второй фазах равны:

G₁ = G₂ (4.5)

Изменение температуры и давления вызовет изменение энергии Гиббса в каждой фазе [см. (2.53)]:

dG₁ = - S₁dT + V₁dP (4.6)

dG₂ = - S₂dT + V₂dP, (4.7)

где V₁, V₂ – молярные объёмы, а S_1, S₂ – молярные энтропии вещества в соответствующих фазах. При равновесии между фазами dG₁=dG₂.

Следовательно,

(S₂ – S₁)dT = (V₂ - V₁)dP, (4.8)

откуда

. (4.9)

Изменение энтропии при температуре фазового перехода

, (4.10)

где ΔН_Ф.П. молярная теплота фазового перехода.

При подстановке (4.10) в уравнение (4.9) получим уравнение

Клапейрона - Клаузиуса:

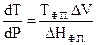(4.11)

Уравнение Клапейрона – Клаузиуса характеризует зависимость температуры фазового перехода от внешнего давления в однокомпонентной системе. В данной форме уравнение применимо к любому двухфазному равновесному переходу.

Для процесса плавления dТ/dР – изменение температуры плавления при изменении давления на единицу. Поскольку плавление всегда сопровождается поглощением тепла, то знак производной dТ/dР зависит от знака ΔV= V_ж – V_тв, то есть изменения объёма при плавлении (следует помнить, что при определении изменения объёма всегда вычитают из конечного значения параметра – начальное). Чаще всего, V_ж > V_тв, поэтому с увеличением давления температура плавления вещества повышается. Реже наблюдается обратная закономерность: ΔV < 0 и с ростом давления температура плавления понижается. Таких веществ не много. Это, например, вода ( при давлениях ниже 2200 атм), висмут и некоторые другие.

Для процесса испарения жидкости уравнению Клапейрона - Клаузиуса можно придать другой вид. Часто можно пренебречь объемом жидкой фазы по сравнению с объемом пара и считать DV=V_п. Например, при 273,15 К для воды V_п = 22400 см³, а V_ж = 18 см³. Если насыщенный пар подчиняется уравнению состояния идеальных газов, то V_п = RT/P (для 1 моля идеального газа) и из (4.11) получим

или

(4.12)

Уравнение (4.12) тоже называется уравнением Клапейрона-Клаузиуса.

Здесь следует снова обратить внимание на то, что под знаком логарифма оказывается величина, имеющая размерность. Не приводя здесь преобразований этой величины в безразмерную, отметим только, что для соблюдения правил применения математического аппарата к вычислениям физических параметров, будем считать, что под знаком логарифма и в этом случае (как и в предыдущем разделе курса, например см. (2.77) и далее) мы подставим относительное давление, то есть давление, отнесённое к Р⁰ – стандартному давлению. Если давление выражено в атмосферах, то Р⁰ = 1 атм.

Для равновесия кристаллы ↔ пар, зависимость давления насыщенного пара вещества, равновесного с кристаллами, от температуры выражается аналогичным уравнением. Тогда вместо DН_исп. следует записать DН_возг. –молярная теплота возгонки, Т – температура возгонки (или сублимации).

Проинтегрируем уравнение (4.12) в пределах от состояния 1 до состояния 2, считая DН_исп. величиной постоянной (не зависящей от температуры):

(4.13)

Или неопределенный интеграл:

(4.14)

Физический смысл постоянной интегрирования В: , где DS_исп. - изменение энтропии при образовании 1 моля пара.

Зависимость линейна, угловой коэффициент ее составляет - DН_исп./2,3R. Для фазовых превращений конденсированных фаз (например, вода↔лед) или полиморфных превращений (например, S_ромб↔S_{монокл.}) температурный коэффициент dP/dT характеризует возникающее давление при изменении температуры на 1 градус. Уравнения Клапейрона-Клаузиуса широко используются при расчете фазовых равновесий.

Пример.

На вершине горы атмосферное давление Р = 634 мм рт. ст. При какой температуре закипит вода в этих условиях? Известно, что теплота испарения воды DН_исп. = 40587 Дж/моль, и при Р₁= 760 мм рт. ст. температура кипения воды Т₁=373 К. Подставив эти данные в уравнение (4.13), рассчитаем Т₂. При заданных условиях вода закипит при Т=368 К, или при 95°С.

Дата добавления: 2014-10-02; просмотров: 574; Нарушение авторских прав

Мы поможем в написании ваших работ!