
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Закон сохранения момента количества движения
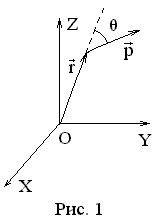 Полный момент количества движения замкнутой системы материальных точек остается.
Полный момент количества движения замкнутой системы материальных точек остается. 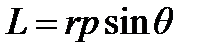 .
. 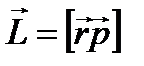 .
.

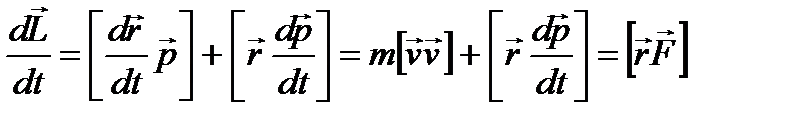 .
.
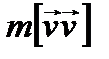 равно нулю по определению векторного произведения
равно нулю по определению векторного произведения
моментом силы и обозначается 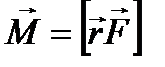 .
.
Таким образом, уравнение, описывающее изменение момента импульса со временем имеет вид:
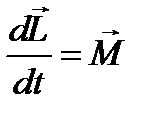
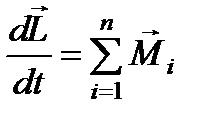 , где
, где 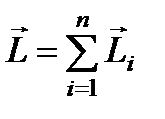 - полный момент импульса системы.
- полный момент импульса системы.
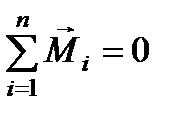 ,
, 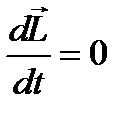 ,
, 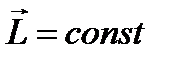 .
.
5.Основной закон вращательного движения твердого тела.
разобьем тело на малые элементы 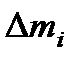 , которые можно считать материальными точками. Тогда для полного момента импульса
, которые можно считать материальными точками. Тогда для полного момента импульса 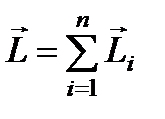 и полного момента сил
и полного момента сил 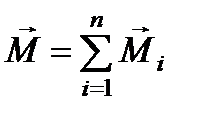 имеем
имеем 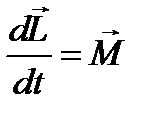
6.Вынужденная прецессия гироскопа.
Вынужденная прецессия гироскопа
При кратковременном воздействии на гироскоп 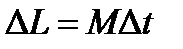 мало по сравнению с
мало по сравнению с 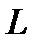 в силу большой угловой скорости вращения вокруг собственной оси. То есть имеет место устойчи-вость движения свободного гироскопа.
в силу большой угловой скорости вращения вокруг собственной оси. То есть имеет место устойчи-вость движения свободного гироскопа.
|
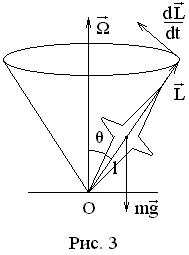
Рассмотрим движение гироскопа с одной неподвижной точкой в поле тяжести (рис. 3).
Будем считать, что 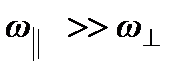 (приближенная теория гироскопа). В этом случае момент импульса гироскопа направлен вдоль его оси и равен
(приближенная теория гироскопа). В этом случае момент импульса гироскопа направлен вдоль его оси и равен 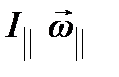 . Основной закон вращательного движения имеет вид:
. Основной закон вращательного движения имеет вид:
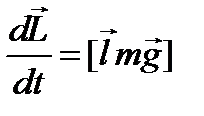 . С другой стороны можно считать, что
. С другой стороны можно считать, что 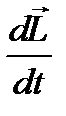
является “скоростью движения” конца вектора 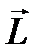 . Тогда по аналогии с формулой
. Тогда по аналогии с формулой 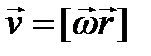 можно записать, что
можно записать, что
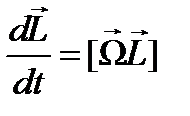 . Отсюда
. Отсюда 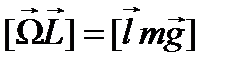 или
или 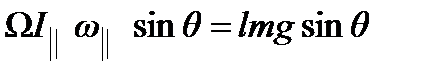 . Отсюда находим
. Отсюда находим
 .
.
8.Гармонические колебания материальной точки. Уравнение осциллятора.
Гармоническое колебание материальной точки – координата точки изменяется по гармони-ческому закону
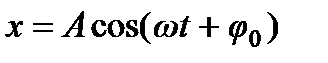 .
.
Здесь 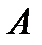 - амплитуда колебания,
- амплитуда колебания, 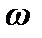 - круговая (циклическая) частота,
- круговая (циклическая) частота, 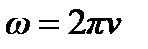 ,
, 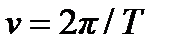 - частота,
- частота, 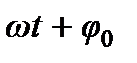 - фаза колебания,
- фаза колебания, 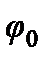 - начальная фаза.
- начальная фаза.
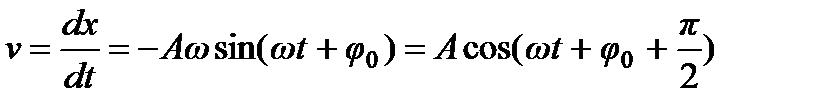 .
.
Ускорение колебательного движения:
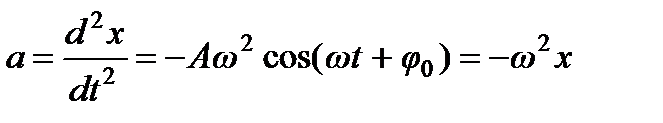 .
.
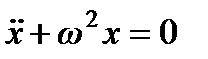 , Уравнение осциллятора
, Уравнение осциллятора
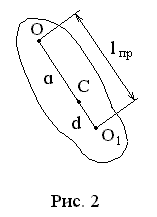
9.Физический маятник. Приведенная длина физического маятника.
Физический маятник – тело, закрепленное на оси, расположенной выше центра масс.
Приведенная длина физического маятника – это длина математического маятника с тем же периодом колебаний, что и у физического. Приравнивая выражения для периодов, получим
|
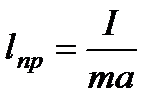 .
.
Обозначим через 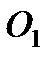 точку, лежащую на продолжении отрезка
точку, лежащую на продолжении отрезка 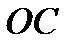 и отстоящую от точки подвеса на расстоянии
и отстоящую от точки подвеса на расстоянии 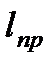 . Точка
. Точка 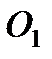 называется центром качаний физического маятника. Можно показать, что физический маятник обладает следующим важным свойством: если физический маятник подвесить за центр качаний, то период его колебаний не изменится.
называется центром качаний физического маятника. Можно показать, что физический маятник обладает следующим важным свойством: если физический маятник подвесить за центр качаний, то период его колебаний не изменится.
10.Затухающие колебания.
не совершив В любой колебательной системе со временем происходит затухание колебаний, обусловлен-ное потерей энергии под действием неконсервативных сил. Рассмотрим затухание колеба-ний материальной точки под действием силы вязкого трения (лекция 10)
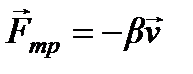 .
.
В этом случае 2-ой закон Ньютона для материальной точки под действием возвращающей сил и силы трения в проекции на ось 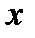 можно представить в виде
можно представить в виде
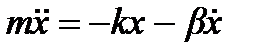 . (1)
. (1)
Коэффициент 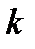 необязательно должен иметь смысл коэффициента жесткости. Он может описывать возвращающую силу любой природы.
необязательно должен иметь смысл коэффициента жесткости. Он может описывать возвращающую силу любой природы.
Можно показать, что при условии 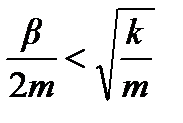 решение уравнения (1) имеет вид
решение уравнения (1) имеет вид
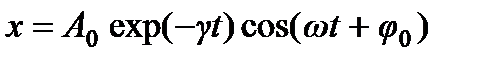 ,
,
где 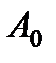 - начальная амплитуда колебаний,
- начальная амплитуда колебаний, 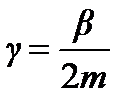 - коэффициент затухания,
- коэффициент затухания, 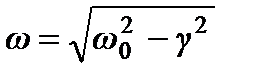 - частота затухающих колебаний,
- частота затухающих колебаний, 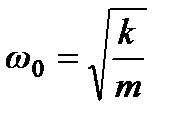 - собственная частота.
- собственная частота.
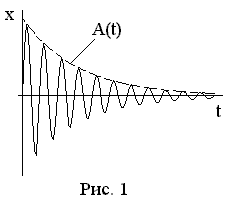
Функция 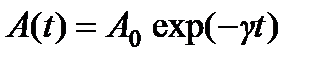 представляет собой амплитуду затухающих колебаний (рис. 1). Для характеристики скорости затухания колебаний вводится логарифмический декремент затухания
представляет собой амплитуду затухающих колебаний (рис. 1). Для характеристики скорости затухания колебаний вводится логарифмический декремент затухания
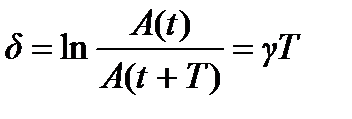 .
.
Затухающие колебания существуют при выполнении условия 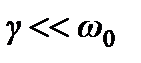 . При
. При 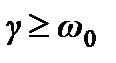 имеет место апериодический процесс, при котором точка возвращается в положение равновесия, ни одного колебания.
имеет место апериодический процесс, при котором точка возвращается в положение равновесия, ни одного колебания.
11. Вынужденные колебания и явление резонанса.
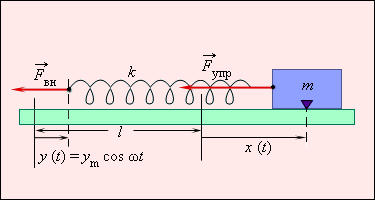
Внешняя сила 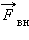 приложена к свободному концу пружины. Она заставляет свободный конец пружины перемещаться по закону
приложена к свободному концу пружины. Она заставляет свободный конец пружины перемещаться по закону
| y = ym cos ωt. |
где ym – амплитуда колебаний, ω – круговая частота.
Второй закон Ньютона для тела массой m принимает вид :
| ma = –kx + kym cos ωt. |
уравнение вынужденных колебаний
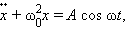
явление резонанса
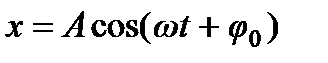 .
.
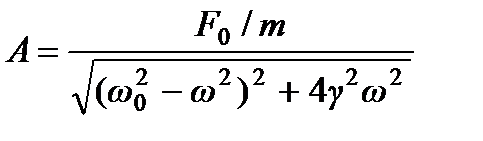 ,
, 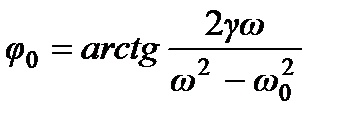 .
.
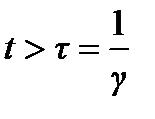
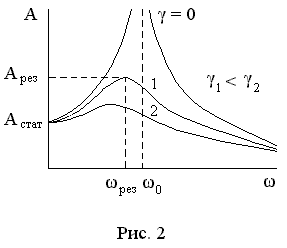
На рис. приведена зависимость амплитуды вынужденных колебаний 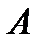 от частоты вынуждающей силы
от частоты вынуждающей силы 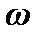 . Амплитуда имеет максимальное значение при
. Амплитуда имеет максимальное значение при
 .
.
Это явление резонанса вынужденных колеба-ний
12. Волны в упругих средах. Уравнение плоской волны.
Волна – процесс распространения колебаний в пространстве.
В волне в упругой среде (газ, жидкость, твердое тело) происходят колебания малых частиц среды.
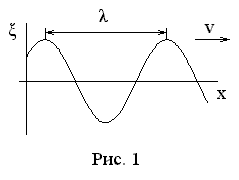
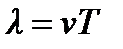 , где
, где 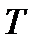 - период колебаний частиц.
- период колебаний частиц.
Уравнением волны называют зависимость
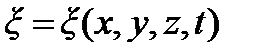 .
.
Получим уравнение плоской волны. Пусть в плоскости 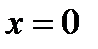 колебания частиц происходят по закону
колебания частиц происходят по закону 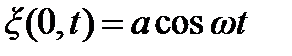 , где
, где 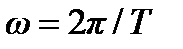 . Через время
. Через время 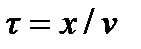 фаза колебаний в точке
фаза колебаний в точке 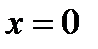 достигнет точки
достигнет точки 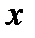 . Следовательно для смещений в точке
. Следовательно для смещений в точке 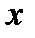 получим
получим
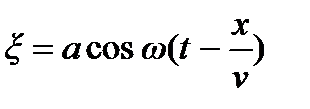 .
.
Это соотношение называется уравнением плоской волны. Для записи уравнения волны удобно ввести волновое число - 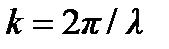 . Тогда
. Тогда 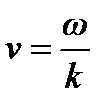 и выражение для
и выражение для 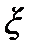 принимает вид:
принимает вид:
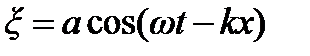 .
.
13. Стоячие волны.
Стоячие волны.
При наличии границ в упругой среде могут возникать колебания особого вида – стоячие волны. Они, например, возникают в натянутой струне с закрепленными концами. Для получения уравнения стоячей волны рассмотрим две одинаковые волны, распростра-няющиеся в противоположных направлениях:
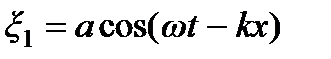 ,
, 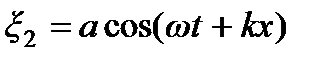 .
.
По принципу суперпозиции для суммарного возмущения имеем
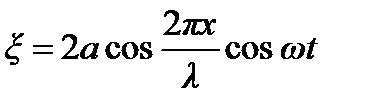 .
.
14. Звуковые волны в газе. Эффект Доплера в акустике.
В газах могут распространяться только продольные волны.
Скорость звука в газе.
Значение скорости звука в газе определяется упругими свойствами этого газа. Скорость звука можно вычислить, используя выражение для скорости волны в упругом стержне 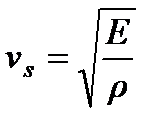 ,
,
Эффект Доплера – изменение частоты при движении источника звука относительно наблюдателя.
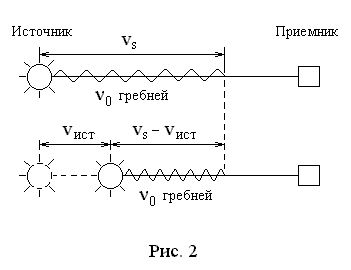
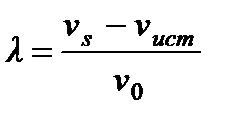 ,
, 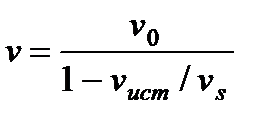 . (2)
. (2)
( 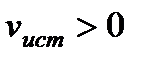 )
)
( 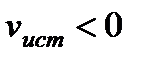 )
)
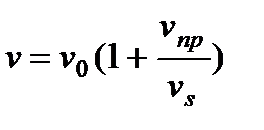 .
. 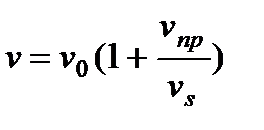 .
.
15. Принципы относительности Галилея и Эйнштейна.
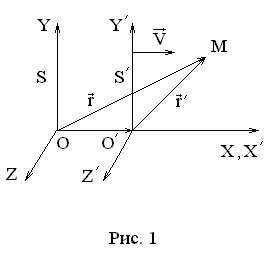
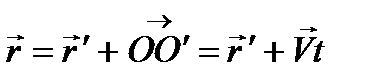 ,
, 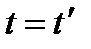 .
.
Принцип относительности Галилея (
Уравнения Ньютона для материальной точки, а также для системы материальных точек одинаковы во все инерциальных системах отсчета (инвариантны относительно преобразований Галилея).
Принцип относительности Эйнштейна.
Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчета относятся эти изменения.
16. Основные положения специальной теории относительности.
Принцип относительности, постулат о постоянстве скорости света и преобразования Лоренца легли в основу специальной теории относительности Эйнштейна (1905 г.), описывающей движение тел при скоростях, сравнимых со скоростью света. Специальной она называется потому, что справедлива только в инерциальных системах отсчета. Для случая произвольных систем отсчета Эйнштейном в дальнейшем была создана общая теория относительности, или релятивистская теория гравитации.
17. Преобразования Лоренца. Законы релятивистской механики.
Преобразования Лоренца:
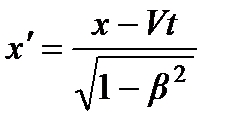 ,
, 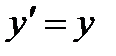 ,
, 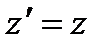 ,
, 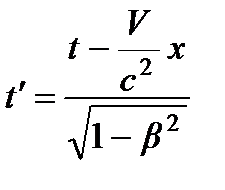 ,
, 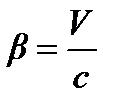 .
.
Преобразования Лоренца оставляют неизменной величину
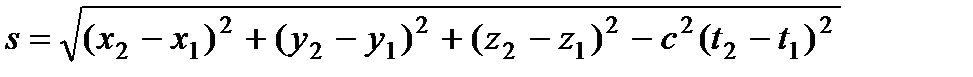 ,
,
называемую интервалом. Ее можно рассматривать как расстояние между двумя точками в четырехмерном пространстве (пространство Минковского) с координатами
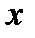 ,
, 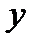 ,
, 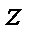 ,
, 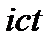 , где
, где 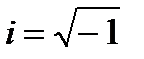 .
.
Для двух инерциальных систем отсчета 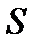 и
и 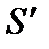 , аналогичных тем, что мы рассмотрели в предыдущей лекции, с помощью преобразований Лоренца можно получить формулу сложе-ния скоростей в релятивистской механике:
, аналогичных тем, что мы рассмотрели в предыдущей лекции, с помощью преобразований Лоренца можно получить формулу сложе-ния скоростей в релятивистской механике:
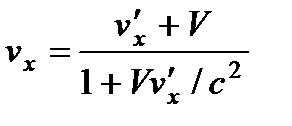 ,
,  ,
, 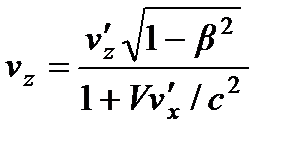 .
.
При 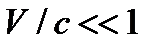 эти выражения переходят в классическую формулу сложения (лекция 1). В случае
эти выражения переходят в классическую формулу сложения (лекция 1). В случае 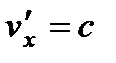 получаем
получаем 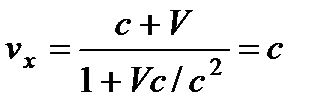 . Этот результат является выражением постулата о постоянстве скорости света во всех инерциальных системах отсчета.
. Этот результат является выражением постулата о постоянстве скорости света во всех инерциальных системах отсчета.
18. Неинерциальные системы отсчета. Центробежная сила и сила Кориолиса.
Движение тел в неинерциальных системах отсчета.
Пусть ускорение материальной точки равно 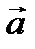 в инерциальной системе отсчета
в инерциальной системе отсчета 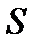 и равно
и равно 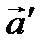 в неинерциальной системе
в неинерциальной системе 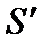 . Рассмотрим разность этих ускорений
. Рассмотрим разность этих ускорений
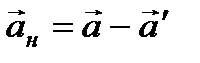 .
.
Для поступательного движения системы 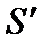 величина
величина 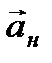 равна ускорению системы
равна ускорению системы 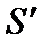 относительно
относительно 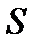 .
.
В инерциальной системе 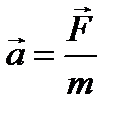 , где
, где 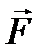 - сила, действующая на материальную точку со стороны некоторого тела. Тогда ускорение
- сила, действующая на материальную точку со стороны некоторого тела. Тогда ускорение 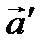 можно представить в виде
можно представить в виде
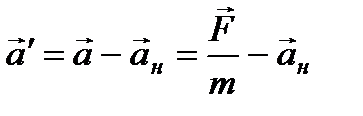 .
.
Умножая это уравнение на массу 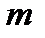 , получим
, получим
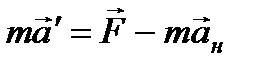 .
.
Для того, чтобы сохранить вид 2-го закона Ньютона в неинерциальной системе отсчета, удобно ввести силу инерции
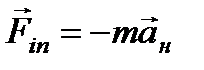 .
.
Тогда 2-ой закон Ньютона в неинерциальной системе можно представить в виде
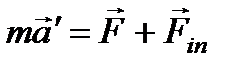 .
.
Сила инерции не является силой по определению, данному в лекции 3. Это некоторое формальное понятие, удобное для описания движения в неинерциальных системах. Однако, как будет видно из дальнейшего рассмотрения, ее проявления являются совершенно реальными.
|
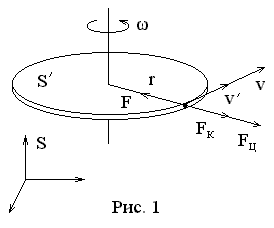
В случае вращательного движения системы 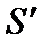 так просто ввести силу инерции уже не удается, так как в этом случае разные точки
так просто ввести силу инерции уже не удается, так как в этом случае разные точки 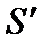 движутся с разным ускорением. Рассмотрим силы инерции во вращающейся системе на простом примере. Будем считать, что система
движутся с разным ускорением. Рассмотрим силы инерции во вращающейся системе на простом примере. Будем считать, что система 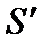 представляет собой равномерно вращающийся с угловой скоростью
представляет собой равномерно вращающийся с угловой скоростью 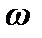 плоский диск радиуса
плоский диск радиуса 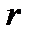 (рис. 1). Пусть материальная точка массы
(рис. 1). Пусть материальная точка массы 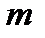 движется по краю диска со скоростью
движется по краю диска со скоростью 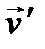 относительно диска. Скорость точки относительно
относительно диска. Скорость точки относительно 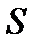 равна
равна
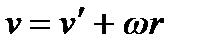 .
.
Ускорение относительно инерциальной системы
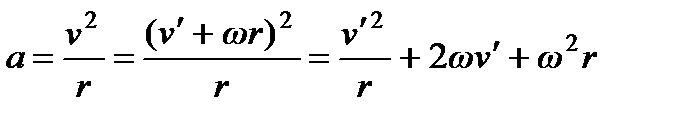 .
.
В неинерциальной системе 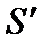
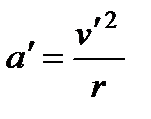 ,
,  .
.
Как следует из опыта, реальная сила, действующая на материальную точку со стороны других тел, не зависит от системы отсчета, то есть 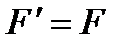 . Тогда последнее уравнение можно переписать в виде
. Тогда последнее уравнение можно переписать в виде
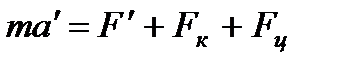 .
.
Здесь 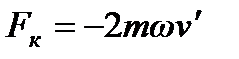 - сила Кориолиса,
- сила Кориолиса, 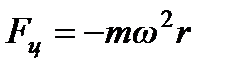 - центробежная сила. Знак минус означает, что в данном случае обе силы направлены в сторону от центра диска. Как видно из этих выражений, во вращающейся системе сила Кориолиса возникает только в случае дви-жения материальной точки в этой системе (
- центробежная сила. Знак минус означает, что в данном случае обе силы направлены в сторону от центра диска. Как видно из этих выражений, во вращающейся системе сила Кориолиса возникает только в случае дви-жения материальной точки в этой системе ( 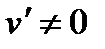 ).
).
19. Закон всемирного тяготения. Законы Кеплера.
| <== предыдущая страница | | | следующая страница ==> |
| Закон сохранения энергии в механике | | | Закон всемирного тяготения Ньютона |
Дата добавления: 2014-11-06; просмотров: 752; Нарушение авторских прав

Мы поможем в написании ваших работ!