Исходные символы языка логики предикатов

Исходные символы языка логики предикатов делятся на шесть групп:

1. V - множество предметных переменных,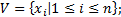

2. С - множество предметных констант,

3. S-множество логических связок, 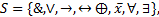здесь 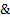- символ конъюнкции или логического умножения, 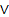-дизъюнкция или логическое сложение, ® символ импликации или логического следования, « - символ эквивалентности, 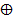– исключающее ИЛИ, 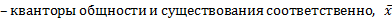- логическое отрицание;

4. F-множество функциональных символов, 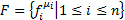, 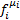– 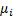-местная функция;

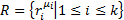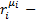
5. R-множество предикатных символов, , 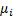- местный предикатный символ.

6. множество вспомогательных символов {, (, ) }.

В языке логики предикатов определяется понятие предметной области D, такой, что 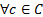с есть наименование объекта в предметной области D; предметные переменные 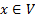«пробега.т» весь диапазон возможных значений из D. Установление связи между элементами языка логики предикатов и предметной областью D производится с помощью функции интерпретации I.

Функциональные символы из множества F суть операции над некоторыми операндами, определенными над предметной областью D.

Предикатные символы есть отношения, определенные также в предметной области D.

Сигнатурой языка логики предикатов называется объединение множеств переменных, функциональных и предикатных символов, которое обозначается как

Здесь

, .

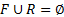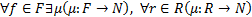Сигнатура называется функциональной, если R 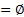и предикатной, если .

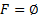Таким образом, отображение ставит в соответствие каждому функциональному символу и каждому предикатному символу натуральное число, являющееся местностью этого функционального или предикатного символа, т.е. определяет число аргументов функционального или предикатного символа. Например, 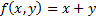определяет двухместный функциональный символ, а выражение 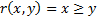– двухместный предикатный символ.

Мощностью сигнатуры 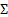называется мощность множества .

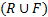Алгебраической системой сигнатуры 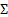, называется упорядоченная пара, содержащая непустое множество D (предметную область) и объекты сигнатуры 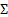,обозначается 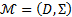, если каждому n-местному предикатному (функциональному) символу из 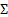сопоставлен n-местный предикат (функция) той же местности на D, а каждой предметной константе из 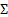сопоставлен некоторый элемент из D. Если сигнатура не содержит функциональных символов, то алгебраическая система называется моделью.

Множество D называется несущим множеством алгебраической системы.

Пусть 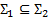, тогда модель 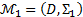называется обеднением модели 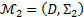. Соответственно, 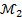есть обогащение 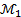, если интерпретация всех символов сигнатуры 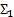совпадает с интерпретацией этих символов в сигнатуре .

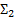При необходимости в модели, может указываться конкретная функция интерпретации для каждого предикатного символа сигнатуры.

Кроме перечисленных исходных символов в логике предикатов рассматриваются еще две категории выражений: термы и формулы.

Индуктивное определение терма:

Термы являются аргументами предикатных символов. Понятие терма сигнатуры 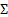определяется индуктивно:

· всякая предметная переменная 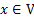и всякая константа 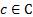являются термом;

· если 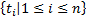– термы, а 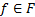– функциональный символ местности n сигнатуры 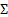, то выражение вида f(t_1,t_2,…,t_n ) –тоже терм

· других термов нет.

Терм называется постоянным (основным, замкнутым), если он не содержит переменных, и параметрическим - в противном случае.

Например, переменные 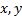и константы 2, е, p- термы, выражения 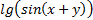– тоже термы.

Индуктивное определение формулы:

· предикатный символ ,где 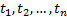термы сигнатуры 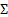, есть атомная формула или атом;

· если 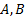– формулы, то ;

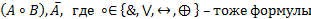· если 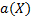– формула, то выражения 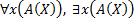– формулы. Здесь 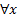и 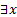называются кванторными приставками, х - переменная кванторной приставки, 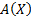– область действия кванторной приставки; в этих случаях говорят, что переменная х входит в формулу связанно, или что имеет место связанное вхождение переменной х;

· других формул нет.

Формула 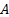называется постоянной или предложением, если она не содержит свободных вхождений переменных. В противном случае формула называется параметрической или условием.

Одна и та же переменная может входить в формулу как связанно, так и свободно. Например,

1. в формулу 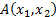обе переменные входят свободно.

2. в формулу 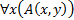переменная x входит связано, а переменная 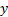– свободно.

3. В формуле 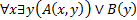переменные x и y входят связанно в первое логическое слагаемое. В формулу 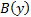переменная 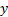входит свободно

Множество формул образует язык логики предикатов PrL.

Дата добавления: 2014-11-08; просмотров: 493; Нарушение авторских прав

Мы поможем в написании ваших работ!