Общезначимые эквивалентности логики предикатов

Логика предикатов изучает свойства операций над предикатами и формул, образованных с помощью этих операций. При этом имеются в виду только такие свойства, которые не зависят от природы элементарных предикатов, входящих в формулы. Поэтому символы элементарных предикатов, входящих в формулы, могут обозначать любые предикаты от соответствующих переменных. Говорят, что символы предикатов, входящих в формулы, являются предикатными переменными в отличие от предметных переменных, от которых эти предикаты зависят. Например, формула 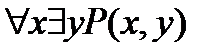содержит один двуместный предикатный символ. При замещении его конкретным предикатом 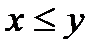, определенным на множестве действительных чисел R, получаем истинное предложение: Для всякого действительного числа х существует большее его действительное число у. При замещении Р предикатом (x>y), определенным также на R, получим истинное предложение: Для всякого действительного числа х существует меньшее его действительное число у.

Главным рабочим инструментом в логике предикатов является понятие эквивалентности формул, которое определяется следующим образом. Формулы А и В эквивалентны, если

множества их свободных переменных совпадают;

при любом замещении входящих в формулы А и В предикатных символов постоянными предикатами эти формулы переходят либо в один и тот же предикат, либо в предложения, имеющие одинаковые таблицы истинности. Разумеется, все вхождения одноименных предикатных символов в А и В должны заменяться одним и тем же предикатом.

Формулы А и В называются равносильными, если их истинностные таблицы совпадают во всех моделях, обозначается А~В. Отношение равносильности есть эквивалентность. Оно разбивает множество формул логики предикатов на классы равносильных формул. Все равносильности языка логики высказываний справедливы также для логики предикатов. Но в логике предикатов появляются новые равносильности, содержащие кванторы. Пусть х, у - переменные, не обязательно разные, А(х,у), В(х), С(х) - формулы, Е - формула, не содержащая свободных вхождений переменной х. Тогда справедливы общезначимые эквивалентности логики предикатов.

Общезначимые эквивалентности:

Замена связанной переменной :

╞ "xB(x) « "yB(y);

╞ $xB(x) « $yB(y).

Перестановка одноименных кванторов:

╞ "x"y A(x,y) « "y"x A(x,y);

╞ $x$yA(x,y) «$y$x A(x,y).

Пронесение отрицания через кванторы:

╞ Ø"xC(x) «$x(ØC(x));

╞ Ø$xC(x) «"x(ØC(x)).

Введение отрицания в формулу:

╞ "xC(x) « Ø($x(ØC(x)));

╞ $xC(x) « Ø("x(ØC(x))).

Дистрибутивность квантора общности относительно конъюнкции:

╞ "xB(x) & "xC(x) «"x(B(x)&C(x)),

╞ E & "xC(x) «"x(E&C(x)).

Дистрибутивность квантора существования относительно дизъюнкции:

╞ $xB(x) Ú$xB(x) « $x(B(x) Ú C(x)),

╞ (E Ú $xC(x)) «$x(E Ú B(x)).

Дистрибутивность квантора существования относительно конъюнкции:

╞ E & $xC(x) «$x(E & C(x)).

Дистрибутивность квантора общности относительно дизъюнкции:

╞ E Ú"xC(x) «"x(E Ú C(x)).

Общезначимые импликации логики предикатов

Правило пронесения квантора существования через конъюнкцию:

╞ ($х (А(х) & В(х)) ®$хА(х) & $хВ(х)).

Правило пронесения квантора общности через дизъюнкцию

╞ ("хА(х) Ú"хВ(х) ®"х(А(х) Ú В(х))).

Смена квантора:

╞ ("х В(х) ®$х В(х));

Перестановка разноименных кванторов:

╞ ($х"у А(х,у)®"у$х А(х,у)).

Приведем пример доказательства общезначимой импликации 4.

Доказательство от противного.

Пусть неверно, что ╞ ($х"у А(х,у)® "у$х А(х,у)). Это возможно, если найдется такая модель, в которой формула $х"у А(х,у) будет истинна, а формула "у$х А(х,у) - ложна. Пусть в предметной области найдется такое значение х=х0, что I["у А(х0,у) ]=1, т.е. "уI[А(х0,у)]=1.

Из предположения о ложности заключения импликации получаем: в предметной области найдется такое значение у=у0, при котором I[$хА(х,у0)] =0, т.е. "х I[А(х,у0)] =0. Следовательно, I[A(x0,y0)]=0. В то же время из предположения об истинности посылки импликации имеем I[A(x0,y0)]=1.

Получение противоречия означает, что предположение о ложности рассматриваемой импликации неверно. Следовательно, общезначимость импликации 4 доказана.

Дата добавления: 2014-11-08; просмотров: 518; Нарушение авторских прав

Мы поможем в написании ваших работ!