
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА: «РЕКУРСИИ»
1.Понятие рекурсии
Рекурсия – это способ определения процесса (или объекта) «в терминах самого себя», в терминах некоторого более простого случая этого же процесса (объекта). Рекурсивные определения используются во многих областях науки, особенно в математике. В математике рекурсией называется способ описания функций или процессов через самих себя. Примером рекурсивно описываемой функции является факториальная функция:
0! = 1;
для всех n>0 n!=n*(n-1)!,
которая для 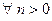 определяется рекуррентным соотношением через значения факториала от (n-1); в свою очередь, (n-1)! Определяется через (n-2)! и т.д. до сведения к значению 0!, которое определено явно и равно единице. Любое рекурсивное описание должно содержать явное определение функции для некоторых (начальных значений аргумента) аргументов, к которому сводится процесс вычисления значения функции в общем случае. Число промежуточных вычислений этой же функции в процессе вычисления ее значения для заданных аргументов (аргумента) – это глубина рекурсии. Для факториальной функции глубина рекурсии при любом значении аргумента очевидна, например, при вычислении 3! Рекурсия имеет глубину в 3 уровня. Однако обычно глубина рекурсии не является столь очевидной даже при простейших описаниях. Примером может служить рекурсивное определение биноминальных коэффициентов или сочетаний
определяется рекуррентным соотношением через значения факториала от (n-1); в свою очередь, (n-1)! Определяется через (n-2)! и т.д. до сведения к значению 0!, которое определено явно и равно единице. Любое рекурсивное описание должно содержать явное определение функции для некоторых (начальных значений аргумента) аргументов, к которому сводится процесс вычисления значения функции в общем случае. Число промежуточных вычислений этой же функции в процессе вычисления ее значения для заданных аргументов (аргумента) – это глубина рекурсии. Для факториальной функции глубина рекурсии при любом значении аргумента очевидна, например, при вычислении 3! Рекурсия имеет глубину в 3 уровня. Однако обычно глубина рекурсии не является столь очевидной даже при простейших описаниях. Примером может служить рекурсивное определение биноминальных коэффициентов или сочетаний 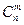 :
:
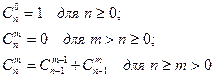
Здесь уже не очевидно, какая глубина рекурсии будет достигнута при конкретных вычислениях. Однако в общем случае можно утверждать, что указанные рекурсивные вычисления требуют конечной глубины рекурсии.
Рекурсивные определения часто используются и в информатике. Например, описание синтаксиса формальных языков с помощью форм Бэкуса-Наура (БНФ-нотаций). В языках программирования рекурсия используется как способ описания подпрограмм (прежде всего функций), содержащих прямо или косвенно обращение к себе самой. Для исполнения таких подпрограмм требуется особая организация вычислительного процесса, так как при рекурсивных вычислениях необходимо сохранение информации об иерархии связей и локальных переменных всех рекурсивных вызовов, чтобы по окончании цепочки рекурсивных вызовов можно было восстановить каждое предшествующее прерванное состояние подпрограммы. Почти все системы рекурсивного программирования основываются на идее стека. Стеком является структура памяти магазинного типа LIFO (Last In First Out) – «последним пришел – первым ушел».
Рекурсия вошла в программирование в значительной степени благодаря системам обработки списков и языкам функционального программирования, где использование рекурсии естественно в силу рекурсивной природы реализуемого вычислительного процесса и рекурсивной структуры обрабатываемых данных. Проникновение рекурсивных методов в практику традиционного (императивного) программирования началось с языка Алгол, допускающего рекурсивные обращения к процедурам. Дальнейшая практика рекурсивных вычислений показала, что разумное применение рекурсии является эффективным методом программирования, существенно упрощает запись многих сложных алгоритмов, в ряде случаев оказывается незаменимым средством. Область практического применения рекурсии – это сложные задачи численного анализа, алгоритмы трансляции, операции над списками, алгоритмы последовательных испытаний и многое другое.
2. Техника построения рекурсивных алгоритмов
В общем случае для правильной организации рекурсивных алгоритмов необходимо выполнение двух условий:
Ø должно быть найдено представление общей задачи в терминах «более простой» задачи того же класса, которое определит последовательность рекурсивных вызовов;
Ø рекурсивные вычисления не должны создавать бесконечную цепочку вызовов; для этого, во-первых, алгоритм должен включать хотя бы одно предписание, в котором при определенных условиях вычисление производится непосредственно, без рекурсивного вызова (терминальную ситуацию), а во-вторых, рекурсивные построения, в конце концов, должны сводиться к этим простым терминальным случаям.
В общем виде рекурсивное описание подпрограммы должно иметь одну из следующих структур или некоторую эквивалентную форму:
| if <условие> then <терминальная ситуация> else <рекурсивные вызовы> | while <условие> do begin <рекурсивные вызовы> end; <терминальная ситуация> |
Существует два разных стиля построения рекурсивных алгоритмов, называемые восходящей и нисходящей рекурсией. Нисходящая рекурсия последовательно разбивает данную задачу на более простые задачи, пока не доходит до терминальной ситуации. Только после этого она начинает строить ответ, а промежуточные результаты передаются обратно вызывающим функциям.
Пример 1. Вычисление факториала.
{Нисходящая рекурсия}
program Factorial;
var n:byte;
function Fact(n:byte):longint;
begin {Fact}
if n=0 then fact:=1 {терминальная ветвь}
else fact:=n*fact(n-1) {рекурсивная ветвь}
end; {Fact}
begin {Factorial}
write(‘Введите n’);
readln(n);
writeln(‘Факториал’,n:2,’=’,fact(n))
end. {Factorial}
Вызов, например, fact(5) означает, что функция fact вызывает себя раз за разом: fact(4), fact(3), … до тех пор, пока не будет достигнута терминальная ситуация. При каждом вызове текущие вычисления «откладываются», локальные переменные и адрес возврата сохраняются в стеке. Терминальная ситуация fact:=1 достигается при n=0. По достижении терминальной ситуации рекурсивный спуск заканчивается, начинается рекурсивный возврат изо всех вызванных на данный момент копий функции: начинает строиться ответ: n*fact(n-1), сохраненные локальные параметры выбираются из стека в обратной последовательности, а получаемые промежуточные результаты: 1*1, 2*1, 3*2*1, 4*3*2*1, 5*4*3*2*1 – передаются вызывающими функциями. Латинское recurrere означает «возвращение назад».
В восходящей рекурсии ответ строится на каждой стадии рекурсивного вызова, получаемые промежуточные результаты вычисляются перед рекурсивным вызовом и передаются в виде дополнительного рабочего параметра подпрограммы до тех пор, пока не будет достигнута терминальная ситуация. К этому моменту ответ уже готов и нужно только передать его вызывающей функции верхнего уровня.
Пример 2. Вычисление факториала.
{Восходящая рекурсия}
program Factorial;
var n:byte;
function Fact(n:byte,w:longint):longint;
begin {Fact}
if n=0 then fact:=w {терминальная ветвь}
else fact:=fact(n-1,n*w) {рекурсивная ветвь}
end;{Fact}
begin {Factorial}
write(‘Введите n’);
readln(n);
writeln(‘Факториал’,n:2,’=’,fact(n,1))
end. {Factorial}
Здесь w – рабочий параметр, применяемый для формирования результата. При первом вызове функции этот параметр надо инициализировать (придать ему начальное значение – 1), далее при каждом рекурсивном вызове, например, при вычислении 5!, он принимает последовательно значения: 5*1, 4*5*1, 3*4*5*1, 2*3*4*5*1, 1*2*3*4*5*1.
Сравнивая нисходящий и восходящий варианты рекурсивного определения факториала, видим: результат вычисляется в разном порядке. Поскольку умножение коммутативно, это не влияет на окончательный ответ. Однако есть классы задач, при решении которых программисту требуется сознательно управлять ходом работы рекурсивных процедур и функций. Такими, в частности, являются задачи, использующие списковые и древовидные структуры данных. Например, при разработке трансляторов применяются так называемые атрибутированные деревья разбора, работа с которыми требует от программиста умения направлять ход рекурсии: одни действия можно выполнить только на спуске, другие – только на возврате. Поэтому понимание рекурсивного механизма и умение управлять им – это необходимые качества квалифицированного программиста.
В следующем примере показана рекурсивная процедура с выполнением действий как до, так и после рекурсивного вызова (с выполнением действий как на рекурсивном спуске, так и на рекурсивном возврате).
Пример 3. Счет от n до 1 на рекурсивном спуске и от 1 до n на рекурсивном возврате. При этом видно, как заполняется и освобождается стек.
{Выполнения рекурсивных действий}
{до и после рекурсивного вызова }
program Stack;
var n:integer;
procedure recursion(i:integer);
begin {Recursion}
writeln(i:30); {Вывод на рекурсивном спуске}
if i>1 then recursion(i-1);
writeln(i:3); {Вывод на рекурсивном возврате}
end; {Recursion}
begin {Strak}
write(‘Введите n:’);
readln(n);
writeln;
writeln(‘Рекурсия:’);
recursion(n)
end. {Stack}
В процедуре Recursion операция writeln(i:30) выполняется перед рекурсивным вызовом, после чего writeln(i:3) освобождает стек. Поскольку рекурсия выполняется от n до 1, вывод по writeln(i:30) выполняется в обратной последовательности: n, n-1,…, 1, а вывод по writeln(i:3) – в прямой: 1, 2, …, n (согласно принципу LIFO – «последним пришел, первым обслужен»).
Возможная глубина рекурсивных вычислений определяется размером используемого стека. Насколько велик стек, можно установить с помощью бесконечной рекурсии. Причем использование директивы {$S+} при переполнении стека приведет к прерыванию программы с выдачей сообщения «Error 202: stack overflow error» («Ошибка 202: переполнение стека»).
Пример 4. Определение размера стека.
{Программа проверки размера стека}
program Stack test;
{$S+} {Включить контроль переполнения стека}
procedure proc(i:integer);
begin {proc}
if i mod 1024=0 then writeln(i:6);
proc(i+1)
end; {proc}
begin {Stack_test}
proc(1)
end. {Stack_test}
Стек связан с другой структурой памяти – с динамической областью. С помощью директивы {$M} можно управлять размером стека.
| <== предыдущая страница | | | следующая страница ==> |
| ПО ГРАЖДАНСКОМУ ПРОЦЕССУ | | | Формы рекурсий |
Дата добавления: 2014-11-15; просмотров: 532; Нарушение авторских прав

Мы поможем в написании ваших работ!