ПРИТЯЖЕНИЕ МОЛЕКУЛ В КОНДЕНСИРОВАННЫХ ТЕЛАХ

Проведем (мысленно) через конденсированное тело две параллельные (например, горизонтальные) плоскости, находящиеся друг от друга на расстоянии чуть большем, чем диаметр молекулы. Все молекулы, центры которых находятся выше (в соответствии с рисунком) верхней проведенной плоскости, притягиваются ко всем молекулам, центры которых находятся ниже нижней проведенной плоскости.

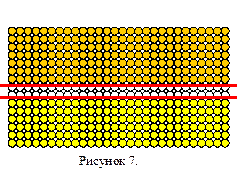
Молекулы между плоскостями сжаты в вертикальном направлении. Поскольку мы можем выбрать ориентацию этих двух плоскостей произвольно, то это означает, что проведенное рассуждение относится к любому направлению (а не только к вертикальному). То есть в любом месте внутри конденсированного тела и в любом направлении существует напряжение сжатия в конденсированном веществе – его и называют внутренним (собственным) давлением в конденсированных телах.

В качестве примера конструкции с внутренним сжимающим давлением можно упомянуть Останкинскую телебашню. Внутри неё натянуты тросы, которые стягивают разные части башни изнутри и не дают башне развалиться при внешних усилиях, создаваемых в основном ветровой нагрузкой.

В модели В-д-В это внутреннее давление зависит от концентрации молекул. Ему соответствует слагаемое a/V² в суммарном давлении.

(P_внешн.+a/V²)(V-b)=RT.

Поскольку мы рассматриваем только конденсированное состояние вещества, а плотность конденсированного вещества при изменении внешних условий меняется мало, то мы будем считать, что величина внутреннего давления остается постоянной при изменении внешнего давления и при изменении температуры вещества.

Как ведут себя молекулы при низкой температуре? Или «Стоп машина!»

При низкой (но не очень, чтобы не проявлялись квантовые эффекты!) температуре кинетическая энергия поступательного и вращательного движения каждой молекулы по величине значительно меньше, чем максимальная глубина потенциальной «ямы», обусловленной взаимодействием двух молекул. Находясь в такой «яме», молекула, имеющая среднюю тепловую кинетическую энергию, не может из нее выбраться. Это так называемое конденсированное состояние вещества. Собираясь вместе, молекулы располагаются так, что каждая из них попадает в несколько потенциальных «ям», созданных ее ближайшими соседками. Быстрый рост потенциальной энергии взаимодействия с уменьшением расстояния между молекулами ограничивает сближение молекул, хотя притяжение к более удаленным молекулам сохраняется. Это можно интерпретировать так, что молекулы имеют некие «размеры» и соответствующий объем, «внутрь» которого другим молекулам «вход закрыт».[4] В этом месте следует напомнить, что большинство молекул не являются сферически симметричными и потенциальная энергия их взаимодействия зависит как от расстояния между молекулами, так и от взаимной ориентации молекул. Это обстоятельство указывает на то, что при низких температурах молекулы не только располагаются в определенных местах в пространстве, но и определенным образом ориентированы по отношению друг к другу. Если взаимная упорядоченность расположения (а в некоторых случаях и ориентации) молекул прослеживаются на расстояниях, значительно превышающих размеры одной молекулы (или атома для простых веществ), (10³ – 10⁶ диаметров молекул) то говорят, что молекулы (или атомы) образуют кристаллическую решетку и вещество находится в кристаллическом состоянии. Если же строгой упорядоченности в расположении молекул нет или она простирается на небольшие расстояния в 10 – 100 диаметров молекул, то говорят, что вещество аморфно.

Столкновения молекул (шариков) друг с другом создают динамическое давление, которое сдерживает вещество от сжатия.

Итак, механическое движение каждой молекулы в составе конденсированного вещества мы рассматриваем, как движение «зверя, запертого в клетке», стенки которой стремятся (под действием внутреннего и внешнего давления) сблизиться. Молекула, ударяясь о стенки собственной клетки, препятствует их сближению. Расстояние от стенки до стенки этой клетки равно: Х + D. Размах колебаний (Х) центра молекулы в составе конденсированного тела обычно гораздо меньше диаметра D молекулы.

Сталкиваясь со стенкой, молекула передает ей импульс 2mV. Давление, которое молекула оказывает на стенки, перпендикулярные выбранному направлению Х, будет вычисляться так же, как оно вычислялось для газа.

P = mV_х²/(ХD²).

Если перейти к средней кинетической энергии, и учесть, что молекула имеет три степени свободы для перемещений, то получится формула, аналогичная формуле для газов:

2/3Е_{кин ср.} 1/(ХD²) = P_int + P_ext

2/3Е_{кин ср.} = (ХD²) (P_int+P_ext) = kT.

Уравнение для большого числа молекул N будет таким:

6. N × (ХD²) × (P_int+P_ext) = RTМ/μ

7. (Х/D)×N D³×(P_int+P_ext) = RTМ/μ

Суммарное давление (внешнее + внутреннее), температура и параметр Х (средний зазор между молекулами) связаны в едином уравнении. Уравнение в форме (7) содержит относительное удлинение (X/D). Если увеличивать внешнее давление при постоянной температуре, то параметр Х (или X/D) уменьшается – это соответствует сжатию вещества. Если при постоянной температуре растягивать вещество, то есть прикладывать к нему отрицательное внешнее давление, то параметр Х увеличивается. Кстати, суммарное давление (P_int+P_ext) при этом все равно остается положительным ([5]). Наконец, если при фиксированном внешнем давлении увеличивать температуру, то параметр Х увеличивается. Уменьшение температуры приводит, соответственно, к уменьшению Х – средних зазоров между молекулами.

Объем конденсированного тела при нулевой температуре V₀, когда можно считать, что зазоров между молекулами нет, равен примерно ND³. При отличной от нуля температуре суммарный объем тела равен примерно N(Х+D)³. Изменение объема равно:

ΔV ≈ 3 (Х/D) ND³ = 3 (Х/D) V₀

В применении к одному молю молекул вещества (М/μ = 1) уравнение «для конденсированного состояния» можно переписать так:

(P_int+P_ext) (V – V₀)/3 = RT.

Это соотношение очень похоже на уравнение В-д-В! Однако есть и существенные отличия:

а) в конденсированном состоянии при низких температурах, когда

V₀>> (V – V₀), нужно вместо (V – V₀), брать объем втрое меньший.

б) величина Pint, добавляющаяся к внешнему давлению Pext, зависит от объема, но при не слишком высоких температурах (много меньших, чем критическая) и при малых внешних давлениях этой зависимостью можно пренебречь, и считать внутреннее давление практически постоянной величиной.

Дата добавления: 2014-11-20; просмотров: 248; Нарушение авторских прав

Мы поможем в написании ваших работ!