Моделирование производственной сферы

Для решения задач по теме «Моделирование производственной сферы» необходимо помнить следующие основные выводы из теоретического материала:

Математическое описание ресурсно-технологических возможностей национальной экономики:

X = (x_i) обозначает вектор затрат ресурсов, i Î М, М = {1, ..., m};

Y = (у_j) — вектор объемов производства, j Î N, N = {1, ..., n}.

Все виды ресурсов можно разбить на два подмножества:

M₁ — воспроизводимые ресурсы (они же продукты), i₁ Î М₁, M₁Ì N;

M₂ — невоспроизводимые ресурсы, i₂ Î М₂. При этом объемы невоспроизводимых ресурсов в каждый данный момент ограничены: Х₂ ≤ R .

Технологическая допустимость пар векторов (X, У) означает возможность получить из затрачиваемых (используемых) ингредиентов вектора X вектор продукции Y. Совокупность всевозможных допустимых технологий (X,Y) образует технологическое множество национальной экономики Z.

Множество производственных возможностей национальной экономики может быть представлено в виде:

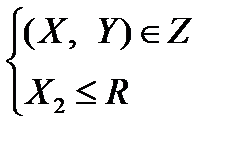
Производственная функция

y_j = f_j(X_j), X_j = (x_1j, ..., x_mj)

характеризует максимально возможный объем выпуска продукта j в зависимости от использования разнообразных ресурсов. Каждой точке X⁰_j соответствует единственный максимальный выпуск y⁰_j.

Различаются два основных типа производственных функций: производственные функции с взаимозаменяемыми ресурсами и производственные функции с взаимодополняемыми ресурсами.

Предположение о взаимозаменяемости ресурсов в производственной функции у_j= f_j(X_j) означает, что один и тот же объем выпуска продукции может быть получен при разных комбинациях ресурсов. Множество точек, удовлетворяющих уравнению постоянного выпуска f(X) = q, называется изоквантой.

Основные характеристики технологии, отображаемой в производственных функциях с взаимозаменяемыми ресурсами:

а) Средняя эффективность ресурса

б) Предельная эффективность ресурса

в) Предельная норма эквивалентной взаимозамены двух ресурсов (h и l) в точке Х⁰:

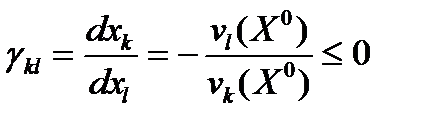
Комбинации ресурсов, для которых предельные нормы эквивалентной замены одинаковы, образуют в пространстве ресурсов кривые, называемые изоклиналями..

г) Эластичность выпуска от затрат различных ресурсов.

Коэффициент эластичности δ_i показывает предельное отношение относительного прироста производства к относительному приросту затрат i-го ресурса:

- в точке X⁰,

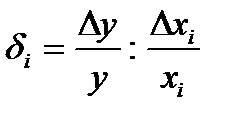- для некоторых интервалов изменения компонент вектора X.

Типовые производственные функции:

1. Однородные производственные функции.

Функция у = f(X) называется однородной n-й степени, если выполняется следующее соотношение:

2. Степенная (мультипликативная) производственная функция:

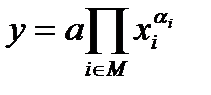
3. Функция с постоянной эластичностью замены ресурсов:

Производственная функция с взаимодополняемыми ресурсами может быть выражена следующим образом:

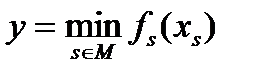
где f_s(x_s) - объем производства, который может быть получен при использовании s-ro ресурса в количестве x_s при условии, что другие ресурсы имеются в достаточном количестве. Максимальный объем производства определяется узким местом, т.е. количеством такого ресурса, который обеспечивает наименьший объем производства.

Изокванты данной функции в пространстве двух ресурсов представляют собой прямые углы.

Функции производственных затрат характеризуют зависимости затрат ресурсов от объемов производства:

x_s =φ_s(y), (sÎM)

φ_s(y) — это минимальное количество ресурса s, которое нужно затратить для выпуска продукта в количестве у. Основными характеристиками функций производственных затрат являются:

· cредние затраты: q_s = x_s/y;

· предельные затраты h_s которые характеризуют прирост затрат ресурса s при увеличении выпуска продукции на "малую единицу": h_s = dx_s/dy.

Типовые функции производственных затрат:

I. Линейная однородная:

x = ay; a > 0

II. Линейная неоднородная функция:

x = ay +b, где а > 0 и b > 0.

III. Нелинейная функция возрастающей эффективности затрат:

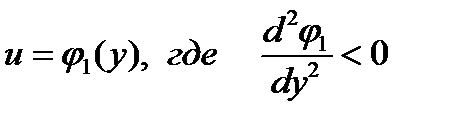
IV. Нелинейная функция падающей эффективности затрат:

Дата добавления: 2014-11-24; просмотров: 328; Нарушение авторских прав

Мы поможем в написании ваших работ!