Пояснения к решению некоторых задач

Задача №1

Дано:

Производственная функция вида

Определить:

К какому классу ПФ относится данная функция?

Является ли она однородной? Докажите. Если функция является однородной, то определите степень однородности.

Решение

Поскольку в данной функции один и тот же объем производства может быть получен при разных комбинациях используемых ресурсов, то функция относится к классу производственных функций с взаимозаменяемыми ресурсами.

Для доказательства однородности функции и определения степени ее однородности воспользуемся общим определением однородных функций:

,

и покажем, что данное соотношение для заданной функции выполняется.

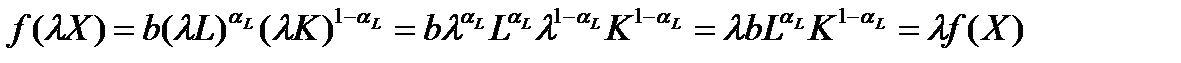
Действительно, основное свойство однородных функций выполняется, следовательно – функция является однородной со степенью однородности 1.

Задача №2

Дано:

Производственная функция вида .

Определить:

Основные характеристики технологии, описываемой данной функцией, а именно: средние и предельные эффективности использования ресурсов, предельную норму взаимозамены ресурсов, эластичность выпуска по ресурсам.

Решение

а) Средняя эффективность ресурса . Для данной функции

б) Предельная эффективность ресурса . Для данной функции

в) Предельная норма эквивалентной взаимозамены двух ресурсов в точке Х⁰:

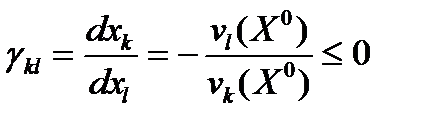
Для данной функции

г) Эластичность выпуска от затрат ресурсов.

. Для данной функции

Задача №3

Дано:

Производственная функция вида: y = min {K/0,2; L/0,4}.

Определить:

· Графически построить изокванты данной функции.

· Вывести на её основе уравнения функций производственных затрат и определить их характеристики (средние и предельные затраты).

Решение

Данная функция относится к классу функций с взаимодополняемыми ресурсами. Изокванты такой функции в пространстве двух ресурсов представляют собой прямые углы. Для графического построения изоквант данной функции необходимо определить их вершины, т.е. точки, в которых достигаются минимальные затраты ресурсов, обеспечивающие определенные объемы производства.

Исходя из условий задачи, минимум затрат обоих ресурсов при производстве продукции в объеме y будет достигнут, когда выполняется равенство:

y = K/0,2 = L/0,4.

В этом случае оба ресурса используются полностью, избытка того или иного ресурса не возникает.

Следовательно:

K/L = 0,2/0,4 = ½ или L = 2K

Иными словами, ресурсы будут использоваться наиболее эффективно, если они используются в соотношении 1:2 (на 1 единицу капитала 2 единицы труда). Все точки в пространстве двух ресурсов, координаты которых соотносятся как 1:2, будут являться вершинами углов изоквант.

L

0 1 2 K

Функции затрат ресурсов будут иметь вид:

K = 0,2y

L = 0,4y

Средние затраты ресурсов:

q_K = 0,2y/y = 0,2

q_L = 0,4y/y = 0,4

Предельные затраты:

h_K = d(0,2y)/dy = 0,2.

h_L = d(0,4y)/dy = 0,4.

Задача №4

Дано:
Функция производственных затрат вида: x = 0,2y.

Определить:

· К какому типу функций производственных затрат она относится

· Её основные характеристики (средние и предельные затраты)

· Изобразить функцию и ее характеристики графически.

Решение

Данная функция производственных затрат относится к типу линейных однородных функций.

Её основные характеристики:

Средние затраты ресурса:

q = 0,2y/y = 0,2

Предельные затраты:

h = d(0,2y)/dy = 0,2.

Изобразим функцию и ее характеристики графически:

x

x = 0,2y

q = h = 0,2

0,2

1 y

Дата добавления: 2014-11-24; просмотров: 506; Нарушение авторских прав

Мы поможем в написании ваших работ!