
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ПОТЕНЦИАЛ, РАЗНОСТЬ ПОТЕНЦИАЛОВ
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ТОЧЕЧНОГО ЗАРЯДА В ПОЛЕ ДРУГОГО ТОЧЕЧНОГО ЗАРЯДА
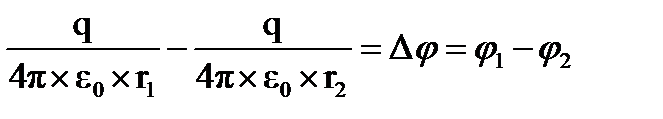 Вычисление работы кулоновской силы уже рассматривалось в разделе «механика». Результат этих вычислений:
Вычисление работы кулоновской силы уже рассматривалось в разделе «механика». Результат этих вычислений: 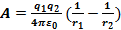 . Будем считать, что заряд q1 – источник электрического поля, в котором движется пробный заряд q2. Отношение работы по перемещению пробного заряда в поле заряда q1 к величине заряда q2 не зависит от величины пробного заряда и поэтому может служить объективной характеристикой поля, создаваемого зарядом q1. Разность потенциалов между начальной и конечной точками перемещения пробного заряда
. Будем считать, что заряд q1 – источник электрического поля, в котором движется пробный заряд q2. Отношение работы по перемещению пробного заряда в поле заряда q1 к величине заряда q2 не зависит от величины пробного заряда и поэтому может служить объективной характеристикой поля, создаваемого зарядом q1. Разность потенциалов между начальной и конечной точками перемещения пробного заряда
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА может быть определен из выражения для разности потенциалов с точностью до некоторой const:
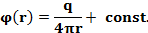
Выбор const:При r→∞ сила кулоновского взаимодействия стремится к нулю, то наиболее естественно положить const=0 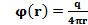 Потенциал поля точечного заряда – это скалярная, энергетическая характеристика поля, равная работе, совершаемой против сил электростатического поля, по перемещению пробного заряда из бесконечности в данную точку поля, отнесенная к величине этого пробного заряда.
Потенциал поля точечного заряда – это скалярная, энергетическая характеристика поля, равная работе, совершаемой против сил электростатического поля, по перемещению пробного заряда из бесконечности в данную точку поля, отнесенная к величине этого пробного заряда.
СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И ПОТЕНЦИАЛОМ
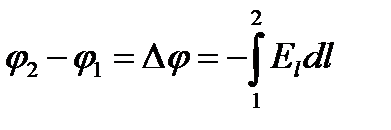 Напряженность электростатического поля и его потенциал используются для характеристики одного о того же объекта - электростатического поля. Связь между ними можно установить, используя выражение для элементарной работы
Напряженность электростатического поля и его потенциал используются для характеристики одного о того же объекта - электростатического поля. Связь между ними можно установить, используя выражение для элементарной работы 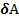 =qErdr =-q dj:
=qErdr =-q dj:
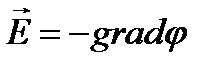
Напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком. Разность потенциалов равна линейному интегралу от напряженности электростатического поля, взятому с обратным знаком.
Лекция №11
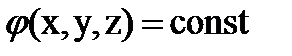 СИЛОВЫЕ ЛИНИИ И ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
СИЛОВЫЕ ЛИНИИ И ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Геометрическое место точек, удовлетворяющее соотношению ,
образует эквипотенциальную поверхность. Силовые линии вектора Е перпендикулярны эквипотенциальным поверхностям.
ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. В отсутствии электрического тока силовые линии не проникают вглубь проводников, а начинаются и оканчиваются на их поверхности. При этом они всегда направлены по нормали к поверхности проводника- проводник представляет собой эквипотенциаль. Если проводник поместить на эквипотенциальную поверхность, то картина взаиморасположения силовых линий и эквипотенциальных поверхностей не изменится за исключением исчезновения поля внутри проводника, что обусловлено появлением индукционных зарядов противоположных знаков на обеих поверхностях проводника. В общем случае, когда в исходном положении разные точки проводника находятся под разным потенциалом, появление индукционных зарядов на поверхности проводника, необходимых для выравнивания потенциала проводящего тела, приводит к существенному искажению исходной картины пространственного распределения силовых линий и эквипотенциальных поверхностей.
СИЛЫ ЗЕРКАЛЬНОГО ИЗОБРАЖЕНИЯ. Задача определения силы взаимодействия точечного заряда с индуцированным зарядом на плоскости достаточно сложна, но она может быть решена простым способом. Если на центральную эквипотенциаль системы, состоящей из двух зарядов одинаковых по величине и противоположных по знаку, поместить проводящую плоскость, то картина распределения силовых линий и эквипотенциальных поверхностей для этих точечных зарядов не изменится. Поэтому характер взаимодействия точечного заряда с проводящей плоской поверхностью эквивалентен взаимодействию двух точечных зарядов (+ заряд как бы «посмотрел» на поверхность и увидел свое изображение как в зеркале)
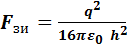
| <== предыдущая страница | | | следующая страница ==> |
| ТЕОРЕМА ГАУССА | | | ЛЕКЦИЯ №12 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ |
Дата добавления: 2014-11-24; просмотров: 255; Нарушение авторских прав

Мы поможем в написании ваших работ!