ТЕОРЕМА ГАУССА

Определение напряженности электростатического поля, создаваемого заряженными телами различной конфигурации с использованием закона Кулона и принципа суперпозиции, является достаточно трудоемкой задачей. Для заряженных тел с высокой степенью симметрии (сферической, цилиндрической и плоской) эта задача решается достаточно просто с помощью теоремы Гаусса

ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. Понятие о потоке абстрактного вектора А через площадку S. Для нахождения этого потока необходимо выделить на площадке S элементарный участок dS, построить вектор А через площадку dS, нормаль n к площадке и найти проекцию вектора А на нормаль к dS. Величина А_ndS- это поток dФ вектора А через элементарную площадку. Интеграл по поверхности S от dФ – это и есть поток Ф вектора А через поверхность S: Ф=∫A_ndS.

В упрощенном выводе теоремы Гаусса источником поля является точечный заряд q, а поверхность интегрирования S- сфера радиусом r, концентричная данному заряду. Оказывается, что полученный при этом результат справедлив в общем случае - для любой замкнутой поверхности произвольной формы и произвольной системы зарядов.

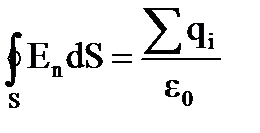
ФОРМУЛИРОВКА ТЕОРЕМЫ ГАУССА: Поток вектора электростатической индукции через замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри поверхности интегрирования, деленной на e₀

ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА ДЛЯ РЕШЕНИЯ ОСНОВНОЙ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ- по заданному распределению зарядов определить напряженность электростатического поля в заданной точке пространства. Использование теоремы Гаусса для определения напряженности электростатического поля имеет смысл только при определенных условиях, налагаемых на поверхность интегрирования: либо силовые линии поля направлены параллельно поверхности интегрирования и тогда поток вектора Е через такую поверхность равен нулю, либо силовые линии поля направлены параллельно поверхности интегрирования и тогда поток вектора Е через такую поверхность равен нулю.

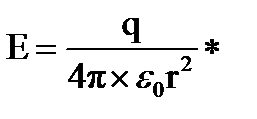
Напряженность поля точечного заряда

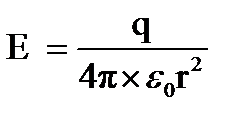
Поле сферы, равномерно заряженной по поверхности. r>R

r<R , Е=0

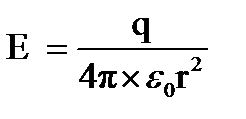
Поле шара, равномерно заряженного по объему r>R

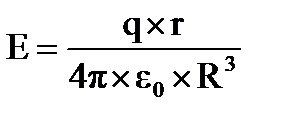
r<R

(при r<R необходимо учитывать только заряды, которые находятся внутри поверхности интегрирования)

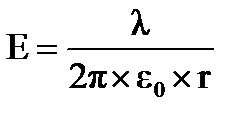
Поле прямой, бесконечной нити (цилиндра), равномерно заряженной по длине

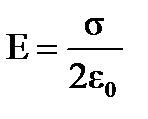
Поле бесконечной плоскости, равномерно заряженной по поверхности

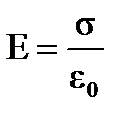Поле двух параллельных бесконечных плоскостей, несущих равномерно распределенный заряд по поверхности, с одинаковой плотностью, но противоположный по знаку (поле плоского конденсатора)

Лекция №10

Дата добавления: 2014-11-24; просмотров: 279; Нарушение авторских прав

Мы поможем в написании ваших работ!