
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ЧИСЛОВЫЕ РЯДЫ
|
Читайте также: |
1. Основные понятия.
Определения.
Выражение вида
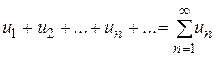 (1)
(1)
называется (бесконечным) числовым рядом.
Числа 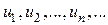 - членами ряда,
- членами ряда, 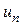 - общим членом ряда, а сумма первых “n” членов
- общим членом ряда, а сумма первых “n” членов 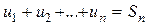 - частичной суммой ряда.
- частичной суммой ряда.
Ряд называется сходящимся, если существует конечный предел последовательности частичных сумм 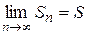 , а число S называется суммой ряда.
, а число S называется суммой ряда.
Если последовательность не имеет конечного предела, то говорят, что ряд расходится. Однако в случае, когда 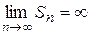 , говорят, что ряд имеет бесконечную сумму.
, говорят, что ряд имеет бесконечную сумму.
Ряд
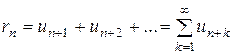 (2)
(2)
называется n-ым остатком ряда (1).
Примеры.
1. Ряд 0+0+0+… сходится, его сумма равна.
2. Ряд 1+1+1+… расходится 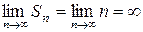 .
.
3. 1-1+1-1+… расходится 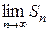 нет.
нет.
4. Ряд 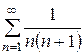 сходится. Его сумма равна 1.
сходится. Его сумма равна 1.
2. Свойства сходящихся числовых рядов.
1. Если сходится ряд (1) и а - некоторое действительное число, то сходится и ряд 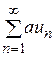 , и его сумма равна aS, т.е. справедливо равенство
, и его сумма равна aS, т.е. справедливо равенство 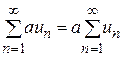 (здесь S - сумма ряда (1)).
(здесь S - сумма ряда (1)).
2. Если сходятся ряды (1) и
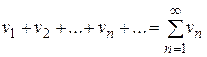 , (3)
, (3)
имеющие, соответственно, суммы S и s, то сходится и ряды 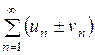 , причём сумма каждого равна (S ±s).
, причём сумма каждого равна (S ±s).
3. Если к ряду прибавить (или отбросить) конечное число членов, то полученный ряд и ряд исходный сходятся или расходятся одновременно.
4. Из сходимости ряда (1) следует сходимость ряда (2) и обратно.
Доказательство следует из свойства 3.
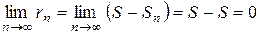
3. Ряд геометрической прогрессии.
Ряд, составленный из элементов геометрической прогрессии
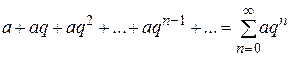 ,
,
сходится при 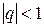 , причём
, причём 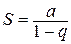 .
.
Расходится при 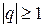 . Его называют рядом бесконечной геометрической прогрессии.
. Его называют рядом бесконечной геометрической прогрессии.
4. Необходимый признак сходимости ряда.
- Если ряд (1) сходится, то 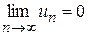 .
.
Следствие (достаточное условие расходимости ряда).
- Если 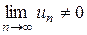 , то ряд расходится.
, то ряд расходится.
Доказывается от противного. Если бы ряд сходился, то 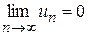 , но это противоречит условию.
, но это противоречит условию.
5. Ряды с положительными членами. Достаточные признаки сходимости.
В дальнейшем будем рассматривать ряды, все члены которых неотрицательны (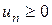 ). Следуя установившейся традиции, такие ряды будем называть рядами с положительными членами или знакоположительными рядами.
). Следуя установившейся традиции, такие ряды будем называть рядами с положительными членами или знакоположительными рядами.
1. Первая теорема сравнения.
Если (1) и (3) два ряда с положительными членами, для которых справедливо равенство 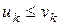
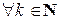 , то из сходимости ряда (3) следует сходимость ряда (1), а из расходимости ряда (1), следует расходимость ряда (3).
, то из сходимости ряда (3) следует сходимость ряда (1), а из расходимости ряда (1), следует расходимость ряда (3).
Замечание.
В качестве ряда сравнения часто берут или ряд, составленный из элементов геометрической прогрессии, или так называемый, обобщённый гармонический ряд 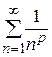 , который сходится при p>1 и расходится при
, который сходится при p>1 и расходится при 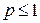 . При p=1 этот ряд называют гармоническим.
. При p=1 этот ряд называют гармоническим.
2. Вторая теорема сравнения. (предельный признак сравнения).
Если существует конечный или бесконечный предел 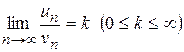 , то:
, то:
а) если 0<k<+¥, то оба ряда одновременно сходятся или расходятся;
б) если k=0, то из сходимости (3) следует сходимость (1);
в) если k=+¥, то из расходимости (3) следует расходимость (1).
3. Признак Даламбера.
Если для членов ряда (1) существует 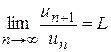 , то этот ряд сходится при L<1 и расходится при L>1. При L=1 о сходимости ряда (1) ничего сказать нельзя (есть как сходящиеся, так и расходящиеся ряды, для которых L=1); в этом случае исследование на сходимость проводится каким-либо иным способом.
, то этот ряд сходится при L<1 и расходится при L>1. При L=1 о сходимости ряда (1) ничего сказать нельзя (есть как сходящиеся, так и расходящиеся ряды, для которых L=1); в этом случае исследование на сходимость проводится каким-либо иным способом.
4. Признак Коши (радикальный).
Если для членов ряда (1) существует 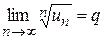 , то этот ряд сходится при L<1 и расходится при L>1. При L=1 о сходимости ряда (1) ничего сказать нельзя (есть как сходящиеся, так и расходящиеся ряды, для которых L=1); в этом случае исследование на сходимость проводится каким-либо иным способом.
, то этот ряд сходится при L<1 и расходится при L>1. При L=1 о сходимости ряда (1) ничего сказать нельзя (есть как сходящиеся, так и расходящиеся ряды, для которых L=1); в этом случае исследование на сходимость проводится каким-либо иным способом.
5. Интегральный признак Коши-Маклорена.
Пусть члены ряда (1) представляют собой значения в целых точках 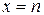 непрерывной невозрастающей на полупрямой
непрерывной невозрастающей на полупрямой 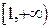 функции f(x):
функции f(x): 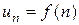 . Тогда:
. Тогда:
1) если сходится 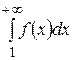 , то сходится и ряд (1);
, то сходится и ряд (1);
2) если расходится 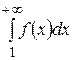 , то расходится и ряд (1).
, то расходится и ряд (1).
6. Произвольные числовые ряды.
Рассмотрим числовой ряд, члены которого могут быть как положительными, так и отрицательными. Такой ряд называется знакопеременным:
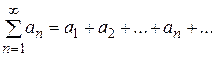 , (4)
, (4)
и ряд, составленный из абсолютных величин его членов
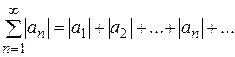 . (5)
. (5)
1. Если ряд (5) сходится, то ряд (4) тоже сходится, и он в этом случае называется абсолютно сходящимся.
2. Если ряд (4) сходится, а ряд (5) расходится, то говорят, что ряд (4) сходится условно.
Для исследования рядов на абсолютную сходимость пользуются признаками сходимости положительных рядов.
Рассмотрим частный случай знакопеременного ряда, так называемый, знакочередующийся ряд.
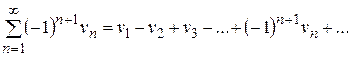 , (6)
, (6)
где 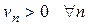 .
.
Теорема Лейбница.
Ряд (6) сходится, если
а) 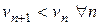 и
и
в) 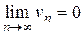 .
.
Ряд вида (6), удовлетворяющий указанным условиям, называется рядом лейбницевского типа или лейбницевским рядом. Остаток лейбницевского ряда имеет знак своего первого члена и меньше его по абсолютной величине: 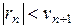 .
.
Предположим, что ряд (4) представим в виде
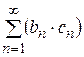 , (7)
, (7)
где 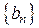 и
и 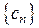 две числовые последовательности. Ряды такого типа можно исследовать на сходимость, если последовательности удовлетворяют некоторым условиям.
две числовые последовательности. Ряды такого типа можно исследовать на сходимость, если последовательности удовлетворяют некоторым условиям.
Признак Абеля.
Если
1) ряд 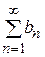 сходится, а
сходится, а
2) 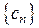 - монотонная и ограниченная последовательность, (т.е. существует число K, такое, что
- монотонная и ограниченная последовательность, (т.е. существует число K, такое, что 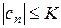 для любого n), то ряд (7) сходится.
для любого n), то ряд (7) сходится.
Признак Дирихле.
Если
1) частичные суммы 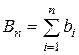 в совокупности ограничены, т.е. найдётся такое число М, что
в совокупности ограничены, т.е. найдётся такое число М, что 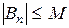 для любого n, а
для любого n, а
2) 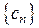 есть монотонная последовательность, стремящаяся к нулю, то ряд (7) сходится.
есть монотонная последовательность, стремящаяся к нулю, то ряд (7) сходится.
лекция 8.
I. Решение примеров (знакоположительные ряды).
1. Найти сумму ряда 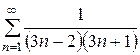 .
.
Решение.
Подсчитаем 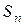 :
:
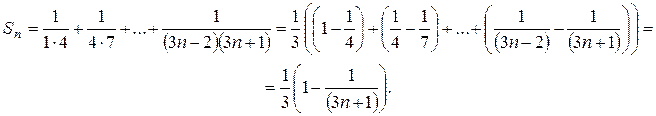
По определению 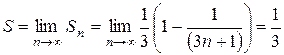 .
.
2. Найти сумму ряда 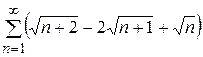 .
.
Решение.
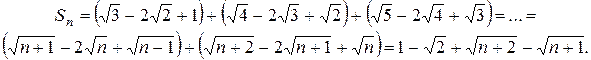
Пользуясь определением суммы ряда и раскрывая неопределённость вида 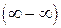 , при вычислении предела, получим:
, при вычислении предела, получим:
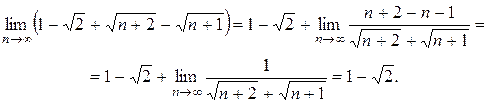
3. Исследовать на сходимость ряд 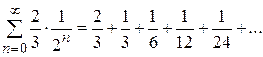 .
.
Решение.
Ряд составлен из членов бесконечно убывающей геометрической прогрессии, в которой 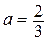 ,
, 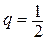 . Следовательно, он сходится,
. Следовательно, он сходится, 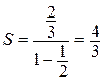 .
.
4. Исследовать на сходимость ряд 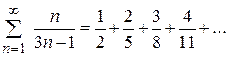
Решение.
Рассмотрим 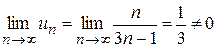 . Ряд расходится, так как не выполняется необходимое условие сходимости (
. Ряд расходится, так как не выполняется необходимое условие сходимости (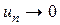 при
при 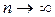 ).
).
5. Исследовать на сходимость ряд 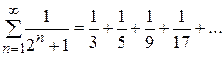
Решение.
Исследуем ряд по первой теореме сравнения. Поскольку 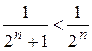 при
при 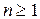 , а ряд
, а ряд 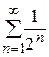 сходится как ряд бесконечно убывающей геометрической прогрессии, то исходный ряд тоже сходится.
сходится как ряд бесконечно убывающей геометрической прогрессии, то исходный ряд тоже сходится.
6. Исследовать на сходимость ряд 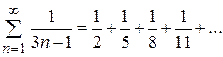 .
.
Решение.
Сравним данный ряд с гармоническим рядом 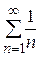 :
:
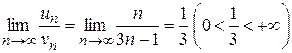 . В силу второй теоремы сравнения он расходится (т.к. расходится гармонический ряд).
. В силу второй теоремы сравнения он расходится (т.к. расходится гармонический ряд).
7. Исследовать на сходимость ряд 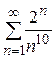 .
.
Решение.
Здесь 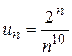 ,
, 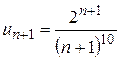 . По признаку Даламбера ряд расходится, поскольку
. По признаку Даламбера ряд расходится, поскольку 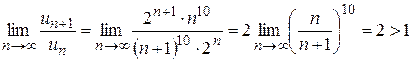 .
.
8. Исследовать на сходимость ряд 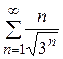 .
.
Решение.
По признаку Даламбера ряд сходится, так как
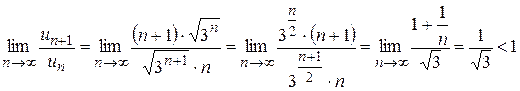 .
.
9. Исследовать на сходимость ряд 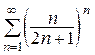 .
.
Решение.
Общий член ряда представляет собой степенно-показательную функцию, поэтому для исследования ряда удобно применить радикальный признак Коши. Так как 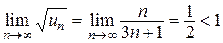 , то ряд сходится.
, то ряд сходится.
10. Исследовать на сходимость ряд 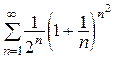 .
.
Решение.
Аналогично предыдущему примеру вычислим
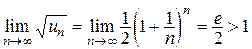 . В соответствии с радикальным признаком Коши, ряд расходится.
. В соответствии с радикальным признаком Коши, ряд расходится.
11. Исследовать на сходимость ряд 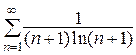 .
.
Решение.
Воспользуемся интегральным признаком Коши-Маклорена. Рассмотрим функцию 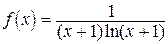 . Эта функция непрерывна, положительна и монотонно стремится к нулю при
. Эта функция непрерывна, положительна и монотонно стремится к нулю при 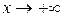 на полуоси
на полуоси 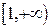 . Несобственный интеграл
. Несобственный интеграл 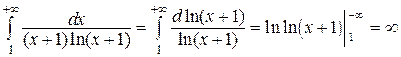 , т.е. расходится. Поэтому расходится и исходный ряд.
, т.е. расходится. Поэтому расходится и исходный ряд.
12. Исследовать на сходимость ряд 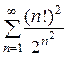 .
.
Решение.
Так как 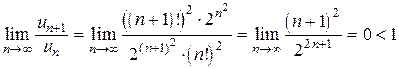 , то
, то
по признаку Даламбера ряд расходится.
13*. Исследовать на сходимость ряд 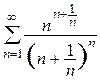 .
.
Решение.
Поскольку
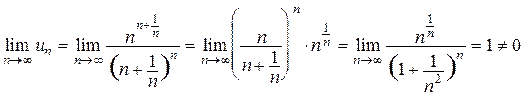 ,
,
то ряд расходится в силу необходимого условия сходимости.
14*. Исследовать на сходимость ряд 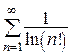 .
.
Решение.
Так как 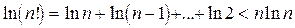 , то
, то 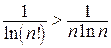 . Значит, исходный ряд сходится согласно признаку сравнения, поскольку ряд
. Значит, исходный ряд сходится согласно признаку сравнения, поскольку ряд 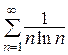 расходится (см. пример 11).
расходится (см. пример 11).
15. Исследовать на сходимость ряд 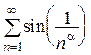 .
.
Решение.
Ряд расходится при 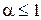 и сходится при
и сходится при 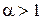 , ибо
, ибо 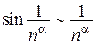 при
при 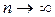 .
.
II. Решение примеров (произвольные числовые ряды)
Исследовать сходимость рядов.
1. 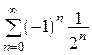 .
.
Решение. Исследуем ряд на абсолютную сходимость. Ряд из абсолютных величин 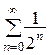 представляет собой сумму членов бесконечно убывающей геометрической прогрессии. Следовательно, он сходится, а исходный ряд сходится абсолютно.
представляет собой сумму членов бесконечно убывающей геометрической прогрессии. Следовательно, он сходится, а исходный ряд сходится абсолютно.
2. 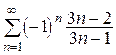 .
.
Решение. Ряд расходится, так как 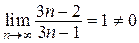 (не выполнено необходимое условие сходимости ряда.)
(не выполнено необходимое условие сходимости ряда.)
3. 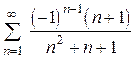 .
.
Решение.
Ряд, составленный из абсолютных величин 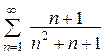 можно сравнить с (расходящимся) гармоническим рядом
можно сравнить с (расходящимся) гармоническим рядом 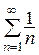 .
.
В самом деле, так как 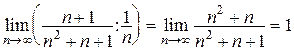 , то ряд
, то ряд 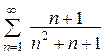 расходится, а исходный ряд абсолютно не сходится. Исследуем его на условную сходимость. Это можно сделать с помощью признака Лейбница:
расходится, а исходный ряд абсолютно не сходится. Исследуем его на условную сходимость. Это можно сделать с помощью признака Лейбница:
1) ряд знакочередующийся;
2) 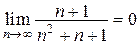 ;
;
3) 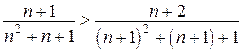 для любого n, так как
для любого n, так как
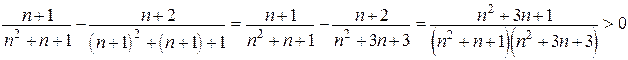 Таким образом, ряд сходится условно.
Таким образом, ряд сходится условно.
4. 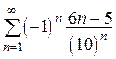 .
.
Решение.
Ряд из абсолютных величин 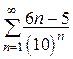 сходится по признаку Даламбера, так как
сходится по признаку Даламбера, так как 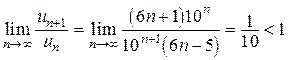 . Значит, данный ряд сходится абсолютно.
. Значит, данный ряд сходится абсолютно.
5. 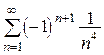 .
.
Решение.
Ряд сходится абсолютно, так как сходится обобщенный гармонический ряд 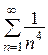 (p=4>1).
(p=4>1).
6. 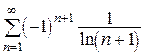 .
.
Решение.
По признаку Лейбница данный ряд сходится, так как 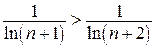 и
и 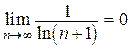 . Но ряд из абсолютных величин
. Но ряд из абсолютных величин 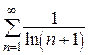 расходится по первой теореме сравнения, ибо
расходится по первой теореме сравнения, ибо 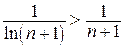 , а ряд
, а ряд 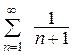 является расходящимся, что нетрудно показать путём сравнения его с гармоническим рядом. Итак, данный ряд сходится условно.
является расходящимся, что нетрудно показать путём сравнения его с гармоническим рядом. Итак, данный ряд сходится условно.
7*. 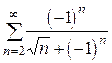 .
.
Решение.
Представим общий член ряда в виде
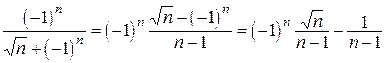 .
.
Так как ряд 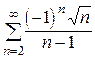 по признаку Лейбница сходится,
по признаку Лейбница сходится,
а ряд 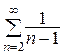 расходится (что нетрудно показать путём сравнения его с гармоническим рядом),
расходится (что нетрудно показать путём сравнения его с гармоническим рядом),
заключаем, что данный ряд также расходится.
8*. 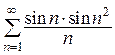 .
.
Решение. Так как
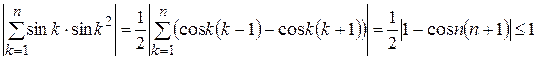
и 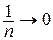 при
при 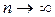 , то, согласно признаку Дирихле, ряд сходится.
, то, согласно признаку Дирихле, ряд сходится.
9*. 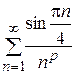 .
.
Решение.
Если 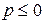 , то ряд расходится ввиду невыполнения необходимого условия сходимости ряда.
, то ряд расходится ввиду невыполнения необходимого условия сходимости ряда.
Если 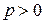 , то ряд сходится по признаку Дирихле, т.к.
, то ряд сходится по признаку Дирихле, т.к.
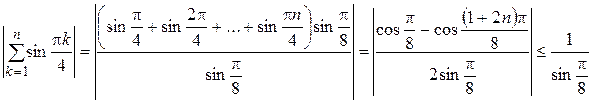 ,
,
а последовательность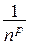 монотонно убывает при
монотонно убывает при 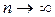 и
и 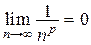 .
.
Для исследования характера сходимости воспользуемся вначале признаком сравнения. Так как 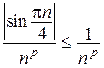 , то ряд сходится абсолютно при
, то ряд сходится абсолютно при 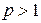 . Характер сходимости ряда на промежутке
. Характер сходимости ряда на промежутке 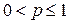 определяет неравенство
определяет неравенство 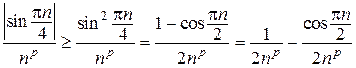 . Ряд
. Ряд 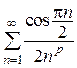 сходится по признаку Дирихле, как и исходный ряд, а ряд
сходится по признаку Дирихле, как и исходный ряд, а ряд 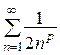 расходится при
расходится при 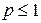 . Поэтому исходный ряд для
. Поэтому исходный ряд для 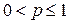 сходится условно. Итак, данный ряд сходится абсолютно при
сходится условно. Итак, данный ряд сходится абсолютно при 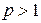 , условно при
, условно при 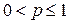 .
.
В примерах 10 и 11 найти сумму ряда.
10. 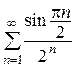 .
.
Решение.
Так как 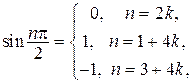 то ряд
то ряд 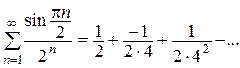 представляет собой сумму членов геометрической прогрессии с первым членом
представляет собой сумму членов геометрической прогрессии с первым членом 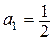 и знаменателем
и знаменателем 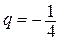 . Следовательно, ряд сходится и сумма
. Следовательно, ряд сходится и сумма 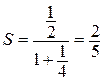 .
.
11. 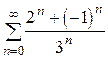 .
.
Решение.
Очевидно, что 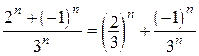 , а каждый из полученных рядов
, а каждый из полученных рядов 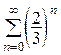 и
и 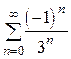 представляет собой сумму членов бесконечно убывающих геометрических прогрессий с
представляет собой сумму членов бесконечно убывающих геометрических прогрессий с 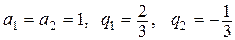 . Сумма ряда
. Сумма ряда 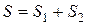 , где
, где 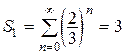 , а
, а 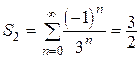 . Следовательно,
. Следовательно, 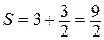 .
.
Примеры для самостоятельного решения.
Исследовать на сходимость следующие числовые ряды.
1. 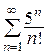 (сходится) 2.
(сходится) 2. 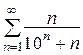 (сходится) 3.
(сходится) 3. 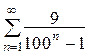 (сходится)
(сходится)
4. 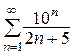 (расходится) 5.
(расходится) 5. 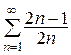 (расходится) 6.
(расходится) 6. 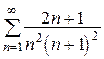 (сходится)
(сходится)
7. 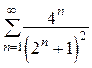 (расходится) 8.
(расходится) 8. 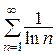 (расходится) 9.
(расходится) 9. 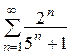 (сходится)
(сходится)
10.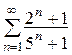 (сходится) 11.
(сходится) 11.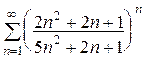 (сходится) 12.
(сходится) 12.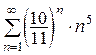 (сходится)
(сходится)
13. 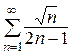 (расходится) 14.
(расходится) 14.  (расходится) 15.
(расходится) 15. 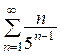 (сходится)
(сходится)
16. 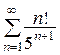 (расходится) 17.
(расходится) 17. 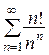 (сходится) 18.
(сходится) 18. 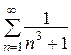 (сходится).
(сходится).
Исследовать на абсолютную и условную сходимость.
1. 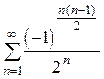 (сходится абсол.) 2.
(сходится абсол.) 2. 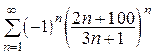 (сходится абсол.)
(сходится абсол.)
3. 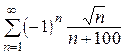 (сходится условно)
(сходится условно)
4. 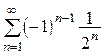 (сходится абсолютно при
(сходится абсолютно при 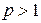 , сходится условно при
, сходится условно при 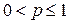 )
)
5. 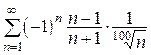 (сходится услов.) 6.
(сходится услов.) 6. 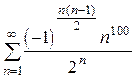 (сходится абсол.)
(сходится абсол.)
7. 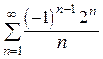 (расходится) 8.
(расходится) 8. 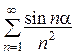 (сходится абсолютно)
(сходится абсолютно)
9. 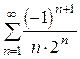 (сходится абсолютно) 10.
(сходится абсолютно) 10. 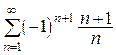 (расходится)
(расходится)
11. 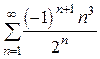 (сходится абс Функциональные ряды.
(сходится абс Функциональные ряды.
Обычный числовой ряд состоит из чисел:
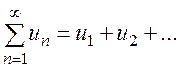
Все члены ряда – это ЧИСЛА.
Функциональный же ряд состоит из ФУНКЦИЙ:
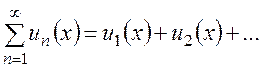 (1)
(1)
В общий член ряда 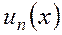 помимо многочленов, факториалов и других «подарков» непременно входит буква «х». Выглядит это, например, так:
помимо многочленов, факториалов и других «подарков» непременно входит буква «х». Выглядит это, например, так:
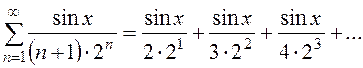
Как видите, все члены функционального ряда – это функции.
Определение.
Если членами ряда будут не числа, а функции, которые определены на некотором множестве X, то ряд называется функциональным. А множество X – областью определения ряда.
Придавая х определённое значение 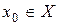 , получим числовой ряд, который может быть как сходящимся, так и расходящимся. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной
, получим числовой ряд, который может быть как сходящимся, так и расходящимся. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной 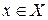 , при которых ряд сходится.
, при которых ряд сходится.
Определение.
Совокупность всех числовых значений аргумента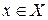 , при которых ряд (1) сходится, называется областью сходимости функционального ряда.
, при которых ряд (1) сходится, называется областью сходимости функционального ряда.
Определение.
Частными (частичными) суммами функционального ряда (1) называются функции 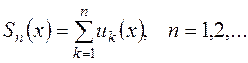
Определение.
Функциональный ряд (1) называется сходящимся в точке х, если в этой точке предел последовательности частичных сумм существует и конечен.
В области сходимости функционального ряда, его сумма является некоторой функцией от х:
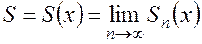 .
.
Пример 1.
Найти область сходимости ряда 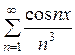 .
.
Решение.
Так как 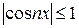 всегда, то очевидно, что
всегда, то очевидно, что 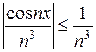 .
.
При этом известно, что общегармонический ряд 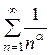 при α =3>1 сходится, то по признаку сравнения исследуемый ряд сходится абсолютно и притом в любом интервале.
при α =3>1 сходится, то по признаку сравнения исследуемый ряд сходится абсолютно и притом в любом интервале.
Пример 2.
Найти область сходимости ряда 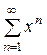 .
.
Решение.
Данный ряд является рядом геометрической прогрессии со знаменателем 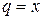 . Следовательно, этот ряд сходится при
. Следовательно, этот ряд сходится при 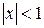 , т.е. при всех
, т.е. при всех 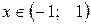 . Сумма ряда равна
. Сумма ряда равна 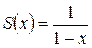 .
.
Степенной ряд.
Наиболее популярной разновидностью функционального ряда является ряд, членами которого являются степенные функции аргумента х, т.е. так называемый - степенной ряд.
Определение.
Степенной ряд – это ряд вида:
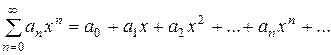 , (2)
, (2)
где числа 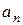 – коэффициенты ряда. Это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «n»).
– коэффициенты ряда. Это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «n»).
Очень часто степенной ряд можно встретить в следующих «модификациях»: 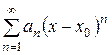 или,
или, 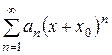 где
где 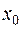 – константа.
– константа.
Строго говоря, такие упрощенные записи степенного ряда не совсем корректны. В показателе степени вместо одинокой буквы «n» может располагаться более сложное выражение, например:
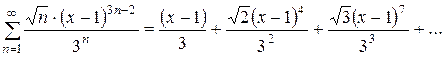
Лишь бы показатели степеней были натуральными.
Ряд, расположенный по степеням 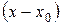 , легко приводится к виду (2), если заменить
, легко приводится к виду (2), если заменить 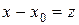
Сходимость степенного ряда.
Интервал сходимости, радиус сходимости и область сходимости
Вся теория степенных рядов основана на лемме Абеля.
Лемма Абеля:
Пусть для некоторого х0 ряд 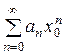 — сходится. Тогда для любого х1, такого, что
— сходится. Тогда для любого х1, такого, что 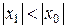 ряд
ряд 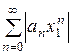 сходится.
сходится.
Рассмотрим степенной ряд 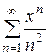 .
.
Переменная 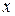 может принимать любое действительное значение.
может принимать любое действительное значение.
Если 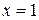 , то
, то 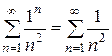 . Если
. Если 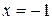 , то
, то 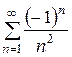 .
.
Если 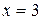 , то
, то 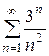 . Если
. Если 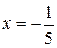 , то
, то 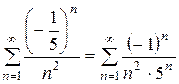 .
.
И так далее.
Очевидно, что мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «x», при которых наш степенной ряд будет сходиться. Такое множество и называется областью сходимости ряда.
Для любого степенного ряда возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале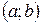 . Иными словами, если мы выбираем любое значение «х» из интервала
. Иными словами, если мы выбираем любое значение «х» из интервала 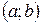 и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал называется интервалом сходимости степенного ряда.
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал называется интервалом сходимости степенного ряда.
Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
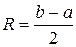 .
.
Геометрически ситуация выглядит так:

В данном случае радиус сходимости ряда:


Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:

Здесь радиус сходимости ряда:
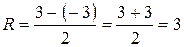
А что будет происходить на концах интервала 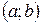 ?
?
В точках 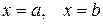 степенной ряд может, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. Речь уже пойдёт не об интервале, а об области сходимости ряда.
степенной ряд может, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. Речь уже пойдёт не об интервале, а об области сходимости ряда.
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: 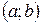
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: 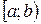 или
или 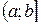 .
.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: 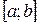
Термины очень похожи, область сходимости ряда – это чуть более детализированный интервал сходимости ряда.
2) Степенной ряд сходится абсолютно при любом значении х. То есть, какое бы значение х мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 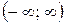 . Радиус сходимости:
. Радиус сходимости: 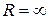 . Рисунок приводить нет необходимости.
. Рисунок приводить нет необходимости.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид (2), то он будет сходиться в единственной точке 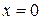 . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: 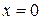 . Если ряд имеет вид
. Если ряд имеет вид 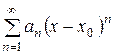 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 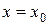 , если ряд имеет вид
, если ряд имеет вид 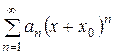 , то в точке
, то в точке 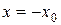 . Радиус сходимости ряда нулевой:
. Радиус сходимости ряда нулевой: 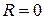 .
.
Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «х», либо интервал 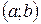 (возможно полуинтервал, отрезок). Данная классификация справедлива только для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
(возможно полуинтервал, отрезок). Данная классификация справедлива только для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
олютно)
Лекция 2
Формулы для нахождения радиуса сходимости степенного ряда.
Для степенного ряда вида (2) радиус абсолютной сходимости можно найти по формулам:
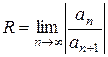 (3)
(3)
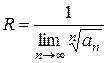 (4)
(4)
Которые легко выводятся из признаков Даламбера и Коши. Тогда

В точке 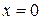 ряд (2) сходится всегда!
ряд (2) сходится всегда!
Интервал сходимости степенного ряда 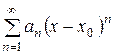 находят из неравенства
находят из неравенства 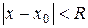 . Он имеет вид
. Он имеет вид 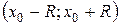 .
.
Если степенной ряд содержит не все степени х т.е. задан не полный степенной ряд, то интервал сходимости ряда находят без формул (3) и (4), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
Основные свойства степенных рядов.
1. Сумма 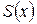 степенного ряда является непрерывной функцией в интервале сходимости.
степенного ряда является непрерывной функцией в интервале сходимости.
2. Степенные ряды, имеющие радиусы сходимости  и
и 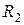 , можно почленно складывать, вычитать и умножать. Радиус сходимости полученных рядов будет не меньше, чем меньшее из чисел
, можно почленно складывать, вычитать и умножать. Радиус сходимости полученных рядов будет не меньше, чем меньшее из чисел  и
и 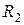 .
.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать.
4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости.
У полученных рядов интервал сходимости не изменится.
Свойства степенных рядов широко используются в теоретических исследованиях и в приближённых вычислениях.
Примеры исследования степенных рядов на сходимость.
Пример 1
Найти область сходимости степенного ряда 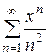 .
.
Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
Решение:
Поскольку этот степенной ряд содержит все степени х т.е. задан полный степенной ряд, то можно найти радиус сходимости по формуле (3):
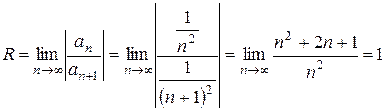
Следовательно,
если 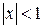 или
или 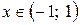 , ряд сходится абсолютно,
, ряд сходится абсолютно,
если 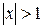 или
или 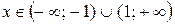 , ряд расходится.
, ряд расходится.
В точках 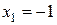 и
и 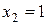 ряд исследуем отдельно.
ряд исследуем отдельно.
1. Пусть 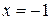 . Степенной ряд будет иметь вид:
. Степенной ряд будет иметь вид: 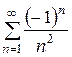 . Это знакочередующийся числовой ряд. Исследуем ряд из модулей:
. Это знакочередующийся числовой ряд. Исследуем ряд из модулей: 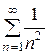 . Он сходится как обобщённый гармонический ряд при
. Он сходится как обобщённый гармонический ряд при 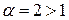 . Следовательно, знакочередующийся ряд сходится абсолютно.
. Следовательно, знакочередующийся ряд сходится абсолютно.
2. Пусть 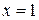 . Степенной ряд будет иметь вид:
. Степенной ряд будет иметь вид: 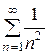 . Он сходится как обобщённый гармонический ряд,
. Он сходится как обобщённый гармонический ряд, 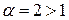 .
.
Ответ: Область сходимости исследуемого степенного ряда: 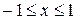 .
.
Пример 2
Найти область сходимости степенного ряда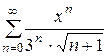
Решение:
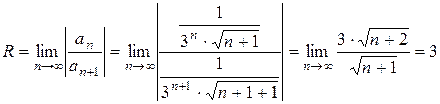 .
.
Следовательно,
если 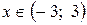 , ряд сходится абсолютно,
, ряд сходится абсолютно,
если 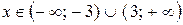 , ряд расходится.
, ряд расходится.
1. Пусть 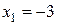 .
.
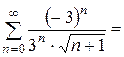
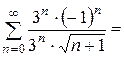
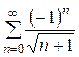 .
.
Это знакочередующийся числовой ряд. Исследуем ряд из модулей: 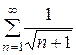 . Он расходится при сравнении с обобщённым гармоническим рядом
. Он расходится при сравнении с обобщённым гармоническим рядом 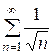 ,
, 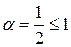 . Следовательно, знакочередующийся ряд не сходится абсолютно.
. Следовательно, знакочередующийся ряд не сходится абсолютно.
Проверим два условия теоремы Лейбница:
1) 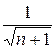
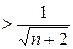 , т.к.
, т.к. 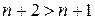 .
.
2) 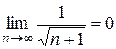 .
.
Оба условия выполнены. Ряд сходится условно в точке 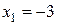 .
.
2. Пусть 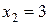 .
.
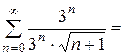
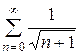 .
.
Сравним его с рядом 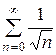 , который расходится как обобщённый гармонический ряд при
, который расходится как обобщённый гармонический ряд при 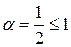 .
.
Рассмотрим 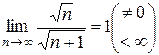 . Следовательно, ряды ведут себя одинаково. Степенной ряд расходится в точке
. Следовательно, ряды ведут себя одинаково. Степенной ряд расходится в точке 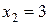 .
.
Ответ: Область сходимости исследуемого степенного ряда – полуинтервал: 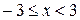 . Причём, в точке
. Причём, в точке 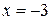 ряд сходится, только условно. Если
ряд сходится, только условно. Если 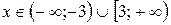 , то ряд расходится.
, то ряд расходится.
Пример 3 (самостоятельно)
Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала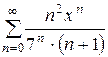
Лекция 3
Пример 4
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала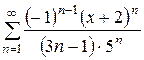
Решение:
В общий член степенного ряда входит множитель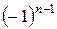 , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела
, обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела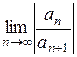 мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Найдем радиус сходимости данного ряда:
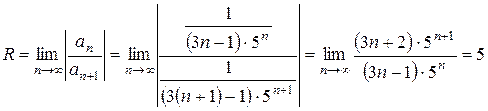
Интервал сходимости степенного ряда находят из неравенства 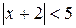 ,
, 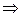
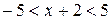 ,
, 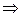
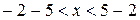 ,
, 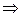
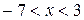 - интервал сходимости исследуемого степенного ряда.
- интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение 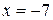 в наш степенной ряд:
в наш степенной ряд:
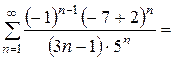

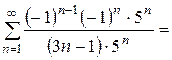
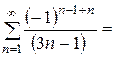
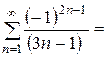
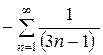
Множитель 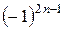 не обеспечивает знакочередование, при любом натуральном «n» он равен «-1». Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда. Рассмотрим ряд
не обеспечивает знакочередование, при любом натуральном «n» он равен «-1». Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда. Рассмотрим ряд
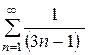 .
.
Он расходится по предельному признаку сравнения, при сравнении его с расходящимся гармоническим рядом.
2) Исследуем второй конец интервала сходимости. При 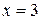
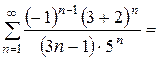
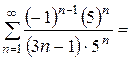
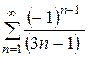
Ряд является знакочередующимся. Используем признак Лейбница:
1) Члены ряда не убывают по модулю и
2) 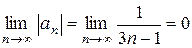
Вывод: ряд сходится условно.
Рассматриваемый числовой ряд не является абсолютно сходящимся. А сходится условно.
Ответ: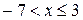 – область сходимости исследуемого степенного ряда, при
– область сходимости исследуемого степенного ряда, при 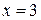 ряд сходится только условно.
ряд сходится только условно.
Пример 5 (самостоятельно)
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала 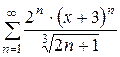
Рассмотрим примеры, в которых степенной ряд не является полным.
Пример 6
Найти область сходимости ряда: 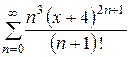
Решение:
Найдем интервал сходимости данного ряда. Используем признак Даламбера:
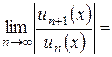
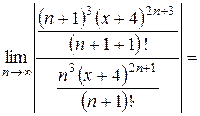
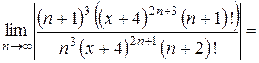
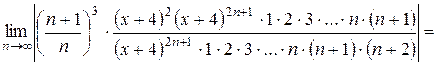
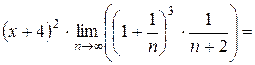
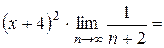
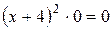
В пределе получен ноль, это меньше единицы для любых значений х, а значит, можно давать окончательный ответ:
Ответ: Ряд сходится по признаку Даламбера при любом значении 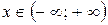 .
.
Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!
Пример 7 (самостоятельно)
Найти область сходимости ряда 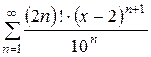
Пример 8
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала 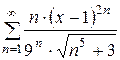
Решение:
Найдем интервал сходимости данного ряда. Используем признак Даламбера:
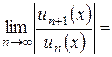
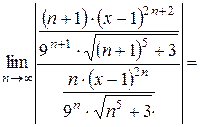

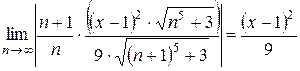
Итак, ряд сходится при 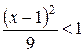 . Умножаем обе части неравенства на 9:
. Умножаем обе части неравенства на 9: 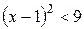 . Извлекаем из обеих частей корень, при этом помним старый школьный приём
. Извлекаем из обеих частей корень, при этом помним старый школьный приём 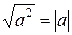 :
:
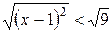 ,
, 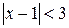
Раскрываем модуль: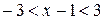
И прибавляем ко всем частям единицу: 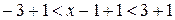 .
.
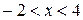 – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если 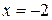 , то получается следующий числовой ряд:
, то получается следующий числовой ряд:
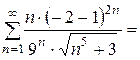
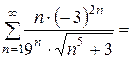
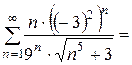
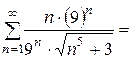
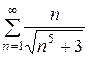 . Для полученного числового ряда следует применить предельный признак сравнения. Какой ряд подобрать для сравнения?
. Для полученного числового ряда следует применить предельный признак сравнения. Какой ряд подобрать для сравнения?
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого: 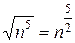 . Таким образом, старшая степень знаменателя равна
. Таким образом, старшая степень знаменателя равна 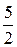 Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:
Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя: 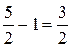 .
.
Таким образом, наш ряд нужно сравнить со сходящимся рядом 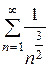 .
.
Используем предельный признак сравнения:
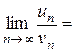
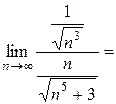
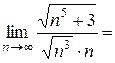

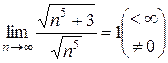
Значит, ряды сходится одновременно.
2) Если 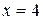 , то получается следующий числовой ряд:
, то получается следующий числовой ряд:
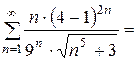
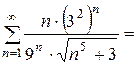
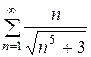
Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область сходимости исследуемого степенного ряда: 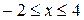 .
.
Пример 9 (самостоятельно)
Найти область сходимости ряда  .
.
В заключение остановимся на одном моменте. Во всех примерах мы использовали признак Даламбера. Всегда ли при решении заданий такого типа нужно применять признак Даламбера? Почти всегда. Однако в редких случаях невероятно выгодно использовать радикальный признак Коши, при этом техника и алгоритм решения задачи остаются точно такими же! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени.
Разложение функций в степенные ряды.
Ряд Тейлора. Ряд Маклорена.
Понятие суммы степенного ряда
Если числовые ряды сходятся к ЧИСЛАМ, то функциональные ряды сходятся к ФУНКЦИЯМ.
Рассмотрим примеры. Простейшее разложение синуса в степенной ряд:
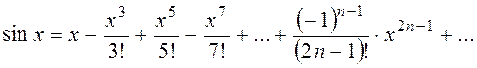
Область сходимости: 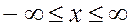 .
.
График функции 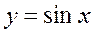 известен из школы:
известен из школы:

Если же начертить график бесконечного многочлена
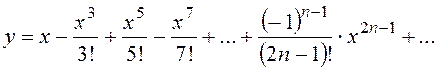 ,
,
то получится… та же самая синусоида!
По признаку Даламбера, этот ряд сходится при любом «х».
А что значит вообще «сходится»?
Если взять первые три члена ряда и начертить график многочлена пятой степени, то он, лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда и начертить его график, то он будет с синусоидой практически совпадать. Чем больше членов ряда – тем лучше приближение.
Рассмотрим ещё пример:
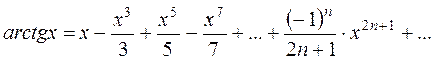
Область сходимости: 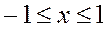
График бесконечного многочлена совпадает с графиком арктангенса только в области сходимости ряда:
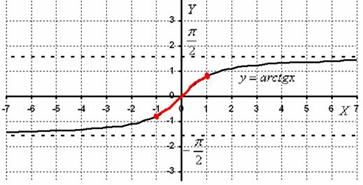
Вне отрезка разложение арктангенса в ряд расходится, а график бесконечного многочлена уходит в бесконечность.
Разложение функций в степенной ряд.
Ряд Тейлора. Ряд Маклорена.
Если функция f(x) имеет непрерывные производные любого порядка в некотором интервале, то ее можно разложить единственным образом в этом интервале в степенной ряд:
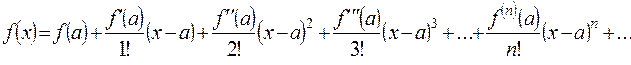 Это формула Тейлора (ударение на первый слог). На практике часто приходится иметь дело с частным случаем формулы Тейлора, когда
Это формула Тейлора (ударение на первый слог). На практике часто приходится иметь дело с частным случаем формулы Тейлора, когда 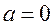 :
:
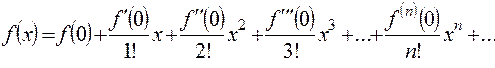
Это разложение называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням 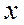 .
.
Выведем разложение экспоненциальной функции:
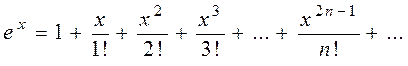
Для формулы Маклорена найдём:
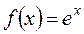 , тогда:
, тогда: 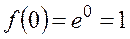
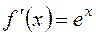 , тогда:
, тогда: 
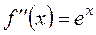 , тогда:
, тогда: 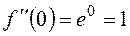
И так далее….
Подставляем единицы в формулу Маклорена и получаем наше разложение!
Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Таблица разложений функций в Ряд Маклорена.
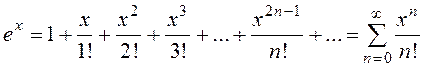 ,
, 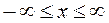 .
.
 ,
,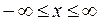
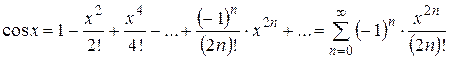 ,
, 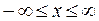 .
.
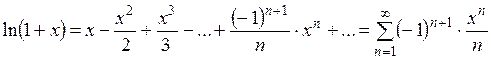 ,
, 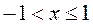 .
.
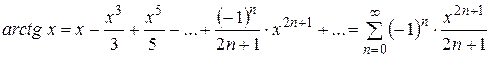 ,
, 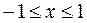 .
.
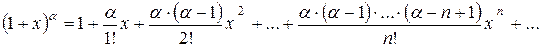 ,
, 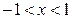 .
.
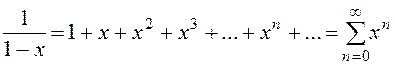 ,
, 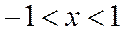 .
.
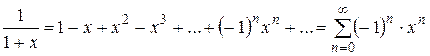 ,
, 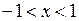 .
.
Примеры разложения функций в ряд Маклорена
Пример
Разложить функцию в ряд Маклорена.
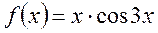
Используем элементарное разложение из таблицы.
В данном случае 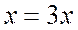
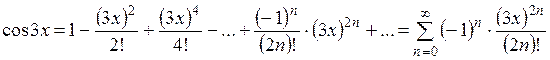
В числителях раскрываем скобки:
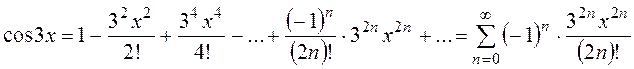
Теперь умножаем на «х»:
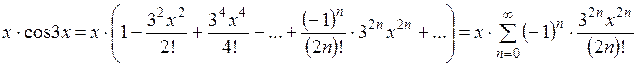
В итоге искомое разложение функции в ряд:
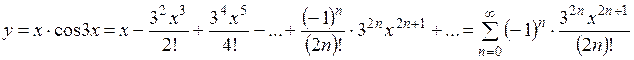
Область сходимости полученного ряда: 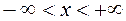
Применение рядов к приближённым вычислениям
Разложение функций в ряд Маклорена необходимо проводить в ряде задач. Мы рассмотрим только одну: приближённое вычисление определённого интеграла.
Пример
Вычислить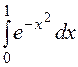 с точностью до 0,001.
с точностью до 0,001.
Воспользуемся разложением 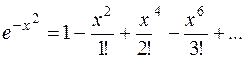
Тогда 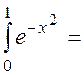
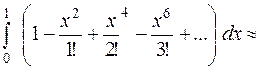
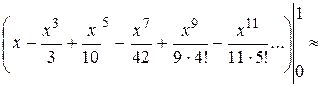 <
<
| <== предыдущая страница | | | следующая страница ==> |
| КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ | | | Дифференциальные уравнения первого порядка |
Дата добавления: 2014-02-28; просмотров: 1108; Нарушение авторских прав

Мы поможем в написании ваших работ!