
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
1. Криволинейный интеграл первого рода, основные понятия и определения
Определение.
Рассмотрим на плоскости или в пространстве дугу кривой L длины l и непрерывную функцию f, определенную в каждой точке дуги l. Разобьем её на части длиной Δli и выберем на каждой из частей точку Mi. Составим интегральную сумму
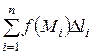 . (1)
. (1)
Назовем λ наибольшую из длин дуг деления. Если существует конечный предел интегральной суммы (1), не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого рода от функции f по кривой L и обозначается
.  (2)
(2)
Теорема.
Если функция z=ƒ(х; у) непрерывна в каждой точке гладкой кривой (в каждой точке существует касательная к данной кривой и положение её непрерывно меняется при перемещении точки по кривой), то криволинейный интеграл первого рода существует и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.
2. Основные свойства криволинейного интеграла I рода
1). Криволинейный интеграл I рода не зависит от направления пути интегрирования, т.е. 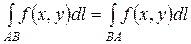 .
.
2).  .
.
3). 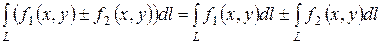
4). 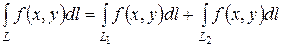 , если путь интегрирования L разбит на части L1 и L2 такие, что L= L1U L2 и L1 и L2 имеют единственную общую точку.
, если путь интегрирования L разбит на части L1 и L2 такие, что L= L1U L2 и L1 и L2 имеют единственную общую точку.
5). Если для точек кривой L выполнено неравенство 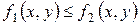 , то
, то 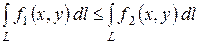 .
.
6). 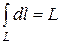
7). Если функция f(x; y) непрерывна на дуге кривой АВ, то на этой дуге кривой найдётся точка (xс; yс):
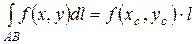 (теорема о среднем).
(теорема о среднем).
3. Вычисление криволинейного интеграла I рода
Явное представление кривой интегрирования.
Если кривая АВ задана уравнением 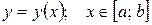 , где
, где  - непрерывно дифференцируемая функция, то
- непрерывно дифференцируемая функция, то
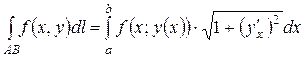 . (3)
. (3)
Параметрическое представление кривой интегрирования.
Если кривая АВ задана уравнениями 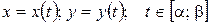 , где
, где 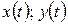 - непрерывно дифференцируемые функции параметра t, причём точке А соответствует t=
- непрерывно дифференцируемые функции параметра t, причём точке А соответствует t= точке В – значение t=
точке В – значение t=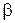 , то
, то
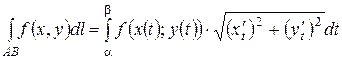 . (4)
. (4)
Полярное представление кривой интегрирования.
Если плоская кривая L задана уравнением 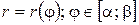 в полярных координатах, то
в полярных координатах, то
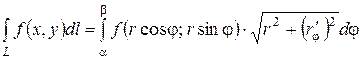 . (5)
. (5)
4. Некоторые приложения криволинейного интеграла I рода
1. Длина кривой 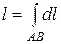 .
.
2. Площадь цилиндрической поверхности 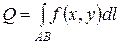 , где АВ, лежащая в плоскости Оху – направляющая цилиндрической поверхности, образующая параллельна оси Oz, f(x; y) – функция, задающая поверхность.
, где АВ, лежащая в плоскости Оху – направляющая цилиндрической поверхности, образующая параллельна оси Oz, f(x; y) – функция, задающая поверхность.
3. Масса материальной кривой (провод, цепь, тросс,…) с линейной плотностью μ(x,y,z)
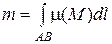 . (6)
. (6)
4. Статические моменты, центр тяжести:
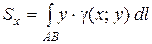 и
и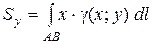 ;
; 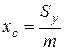 и
и 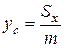 . (7)
. (7)
5. Моменты инерции для материальной кривой АВ относительно осей Ох, Оу и начала координат:
 ,
, 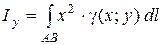
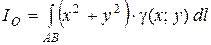 . (8)
. (8)
5. Криволинейный интеграл второго рода, основные понятия и определения
Определение.
Рассмотрим на плоскости или в пространстве дугу кривой L длины l и непрерывную функцию Р(х,у), определенную в каждой точке дуги l. Разобьем её на части длиной Δli в направлении от точки А к точке В, и выберем на каждой из частей точку Mi. Составим интегральную сумму
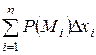 , (9)
, (9)
где 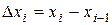 - проекция дуги li на ось Ох.
- проекция дуги li на ось Ох.
Сумму (9) называют интегральной суммой для функции Р(х, у) по переменной х. Таких сумм можно составить бесчисленное множество. (Отличие (9) от (1) очевидно.)
Назовем λ наибольшую из длин дуг деления. Если существует конечный предел интегральной суммы (9), не зависящий ни от способа разбиения кривой АВ на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом по координате х (II рода ) от функции P по кривой L и обозначается
. 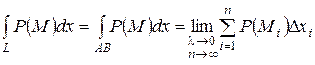 (10)
(10)
Аналогично вводится криволинейный интеграл от функции Q(х,у), по координате у:
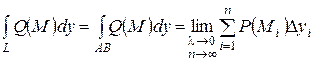 , (11)
, (11)
где 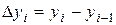 - проекция дуги li на ось Оу.
- проекция дуги li на ось Оу.
Криволинейный интеграл II рода общего вида определяется равенством:
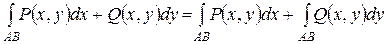 (12)
(12)
Теорема.
Если кривая АВ гладкая, а функции Р(х,у) и Q(х,у) непрерывные на кривой АВ, то криволинейный интеграл II рода существует.
6. Основные свойства криволинейного интеграла II рода
1). При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т.е.
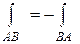 (13)
(13)
(проекции дуги на оси меняют знаки с изменением направления).
2). 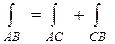 . (14)
. (14)
3). Если кривая АВ лежит в плоскости, перпендикулярной оси Ох, то
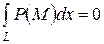 (все
(все  ). (15)
). (15)
4). Криволинейный интеграл II рода по замкнутой кривой (обозначается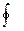 ) не зависит от выбора начальной точки (зависит только от направления обхода кривой).
) не зависит от выбора начальной точки (зависит только от направления обхода кривой).
7. Вычисление криволинейного интеграла II рода
Явное представление кривой интегрирования.
Если кривая АВ задана уравнением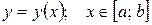 , где
, где  - непрерывно дифференцируемая функция, то
- непрерывно дифференцируемая функция, то
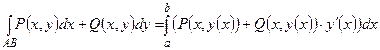 (16)
(16)
Параметрическое представление кривой интегрирования.
Если кривая АВ задана уравнениями 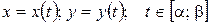 , где
, где 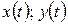 - непрерывно дифференцируемые функции параметра t, причём точке А соответствует t=
- непрерывно дифференцируемые функции параметра t, причём точке А соответствует t= точке В – значение t=
точке В – значение t=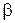 . И пусть функция Р(х,у) и Q(х,у) непрерывны на ней, тогда
. И пусть функция Р(х,у) и Q(х,у) непрерывны на ней, тогда
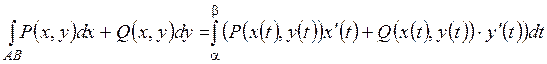 (17)
(17)
8. Формула Остроградского-Грина
Связь между двойным интегралом по области D и криволинейным интегралом по границе односвязной области.
Множество точек (на прямой, на плоскости, в пространстве) называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.
Примеры: односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.
Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.
Теорема 1
Если функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными 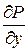 и
и  в области D, то имеет место формула
в области D, то имеет место формула
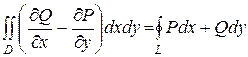 (формула Остроградского-Грина) (18)
(формула Остроградского-Грина) (18)
L – граница области D и интегрирование вдоль кривой L производится в положительном направлении (т.е. при движении вдоль кривой, область D остаётся слева).
Теорема 2
Для того чтобы криволинейный интеграл 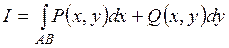 не зависел от пути интегрирования в односвязной области D, в которой функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными
не зависел от пути интегрирования в односвязной области D, в которой функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными 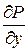 и
и  , необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие
, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие 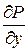 =
= .
.
Следствие.
Если выполняется условие 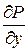 =
= , то интеграл по замкнутому контуру равен нулю.
, то интеграл по замкнутому контуру равен нулю. 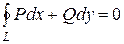 . Верно и обратное утверждение.
. Верно и обратное утверждение.
9. Некоторые приложения криволинейного интеграла II рода
1. Площадь плоской фигуры ограниченной замкнутой линией L можно найти по формуле
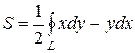 (19)
(19)
при этом L обходится против часовой стрелки.
2. Работа переменной силы 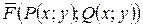 на криволинейном участке АВ производит работу, которая находится по формуле
на криволинейном участке АВ производит работу, которая находится по формуле
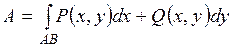 .
.
Определение. Криволинейный интеграл, представляющий собой работу векторного поля вдоль некоторой кривой L называется линейным интегралом от вектора 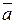 по ориентированной кривой L.
по ориентированной кривой L.
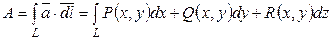 .
.
| <== предыдущая страница | | | следующая страница ==> |
| ДВОЙНОЙ ИНТЕГРАЛ | | | ЧИСЛОВЫЕ РЯДЫ |
Дата добавления: 2014-02-28; просмотров: 784; Нарушение авторских прав

Мы поможем в написании ваших работ!