
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ДВОЙНОЙ ИНТЕГРАЛ
1. Основные понятия и определения
 Определение.
Определение.
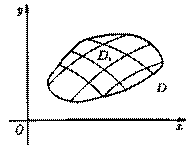
1. Пусть в замкнутой области (области с границей) D плоскости хОу задана непрерывная функция z=ƒ(х;у).
2. Разобьем область D на n «элементарных областей» 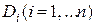 , площади которых обозначим через ΔSi, а диаметры (наибольшее расстояние между точками области) - через di..
, площади которых обозначим через ΔSi, а диаметры (наибольшее расстояние между точками области) - через di..
3. В каждой области Di выберем произвольную точку Mi (xi;yi), умножим значение ƒ(хi;уi) функции в этой точке на ΔSi и составим сумму всех таких произведений:
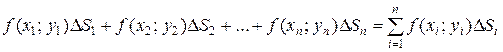 (1)
(1)
Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.
4. Рассмотрим предел интегральной суммы (1), когда n стремится к бесконечности таким образом, что max di 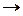 0. Если этот предел существует, конечен и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается
0. Если этот предел существует, конечен и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается
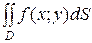 (или
(или 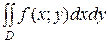 )
)
Таким образом, двойной интеграл определяется равенством
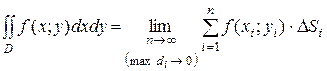 (2)
(2)
В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.
Для всякой ли функции существует двойной интеграл? Каковы необходимые и достаточные условия его существования?
Теорема 1 (необходимое условие интегрируемости функции).
Если функция z=ƒ(х; у) интегрируема по области D, то она ограничена в этой области.
Теорема 2 (достаточное условие интегрируемости функции).
Если функция z=ƒ(х; у) непрерывна в ограниченной замкнутой области D, то она интегрируема по этой области.
На самом деле, функция интегрируема при менее жестких ограничениях:
Теорема 3.
Ограниченная функция, имеющая конечное число точек и линий (спрямляемых, т.е. конечной длины) разрыва в области D, интегрируема по этой области.
2. Основные свойства двойного интеграла
Перечислим без доказательства основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
1). 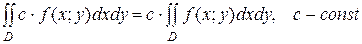 - линейность
- линейность
2). 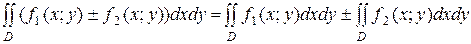 - линейность.
- линейность.
3). Если область D разбить линией на две области D1 и D2 такие, что 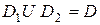 , а пересечение D1 и D2 состоит лишь из линии, их разделяющей, то
, а пересечение D1 и D2 состоит лишь из линии, их разделяющей, то
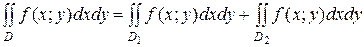 - аддитивность.
- аддитивность.
4). Если в области D имеет место неравенство ƒ(х; у) 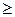 0, то и
0, то и  . Если в области D функции ƒ(х;у) и
. Если в области D функции ƒ(х;у) и 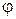 (х;у) удовлетворяют неравенству
(х;у) удовлетворяют неравенству 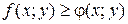 , то и
, то и  интегрирование неравенств.
интегрирование неравенств.
5). 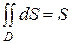 , Так как
, Так как 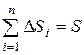 .
.
6). Если функция ƒ(х; у) непрерывна в замкнутой области D, площадь которой S, то 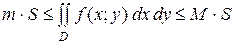 , где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
, где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
7). Если функция ƒ(х;у) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (хо; уо), что 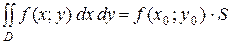 .
.
Величину 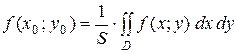 называют средним значением функции ƒ(х; у) в области D.
называют средним значением функции ƒ(х; у) в области D.
3. Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
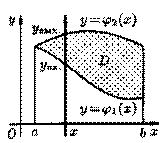
1. Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=φ1(x) и у=φ2(х), причем функции φ1(x) и φ2(х) непрерывны и таковы, что φ1(x) ≤ φ2(х) для всех х є [а; b] (см. рис). Такая область называется правильной в направлении оси Оy
Определение.
Назовем область D правильной в направлении оси Оy, если она
1. ограничена: сверху — графиком только одной функции 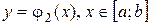 , снизу — графиком только одной функции
, снизу — графиком только одной функции 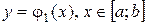 .
.
2. любая прямая, параллельная оси Oy и проходящая через внутреннюю точку области D пересекает ее границу только в двух точках.
При таких областях интегрирования, двойной интеграл вычисляется по формуле:
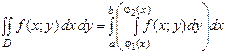 (3)
(3)
Формула (3) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (3) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.
При этом 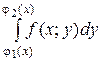 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
2. Если же область D ограничена прямыми y=c и y=d (c<d), кривыми x=Ψ1(у) и х=Ψ2(у), причем Ψ1(у)≤Ψ2(у) для всех у є [с; d], т. е. область D - правильная в направлении оси Оx, то аналогично получим:
 (4)
(4)
Замечания.
1. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (3), так и по формуле (4).
2, Если область D не является правильной (верхняя или нижняя граница интегрирования внутреннего интеграла не записывается одной формулой, или любая прямая, параллельная оси Oy (Ox) и проходящая через внутреннюю точку области D пересекает ее границу более, чем в двух точках), то для сведения двойного интеграла к повторным область D следует разбить на части, правильные в направлении оси Оу или оси Ох.
3. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные. Внутренние пределы постоянны только для координатного прямоугольника. Внутренние пределы интегрирования могут зависеть только от внешней переменной.
Примеры.
1. Вычислить повторный интеграл 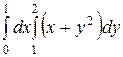 (Отв.
(Отв. 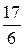 )
)
2. По какой переменной взят внешний интеграл? Написать уравнения кривых, ограничивающих область интегрирования и построить эту область:
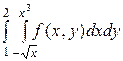
3. D: у = х, у = х-3, у = 2, у = 4. Записать 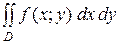 в виде повторных в различных порядках.
в виде повторных в различных порядках.
 4. Изменить порядок интегрирования:
4. Изменить порядок интегрирования: 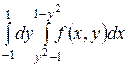
5. Вычислить 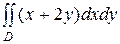 , где область D: у =x2, у=0, х+у-2=0.
, где область D: у =x2, у=0, х+у-2=0.
4. Замена переменных. Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
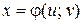 и
и 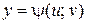 (5)
(5)
Если функции (5) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
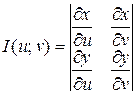 , (6)
, (6)
а функция ƒ(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
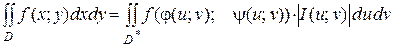 (7)
(7)
Функциональный определитель (6) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и .
В качестве u и υ возьмем полярные координаты r и . Они связаны с декартовыми координатами формулами х=rcos , у=r sin .
Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (6)
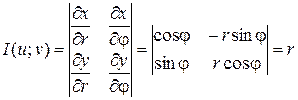 .
.
Формула замены переменных (7) принимает вид:
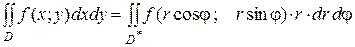 (8)
(8)
где D* - область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу.
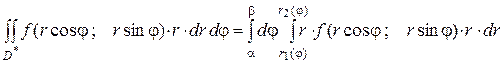 (9)
(9)
Замечания.
1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ƒ(х2+у2); область D есть круг, сектор, кольцо. При расстановке пределов в полярных координатах r обычно считают внутренней переменной, а φ − внешней.
2. В случае эллиптической области выгоднее использовать обобщенные полярные координаты: х=arcos, у=brsin, dxdy=abrdr  d.
d.
Пример.
Вычислить 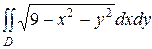 , где область D - круг
, где область D - круг 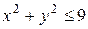 .
.
Решение: Применив формулу (8), перейдем к полярным координатам:
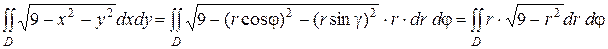
Область D в полярной системе координат определяется неравенствами (см. рис) 0≤≤2,0≤r≤3. Заметим: область D - круг - преобразуется в область D* - прямоугольник. Поэтому, согласно формуле (9), имеем:
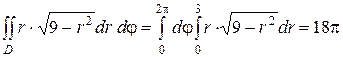 .
.
5. Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
1. Объем тела (геометрический смысл двойного интеграла)
Объем цилиндрического тела находится по формуле
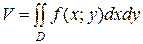 (10)
(10)
где z=ƒ(х; у)>=0 - уравнение поверхности, ограничивающей тело сверху.
2. Площадь плоской фигуры
Если положить в формуле (10) ƒ(х; у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
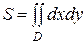 (11)
(11)
3. Масса плоской фигуры (физический смысл двойного интеграла)
Масса плоской пластинки D с переменной плотностью =(х; у) находится по формуле
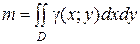 (12)
(12)
4. Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу могут быть вычислены по формулам
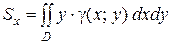 и
и 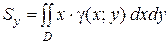 (13)
(13)
а координаты центра масс фигуры - по формулам
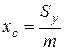 и
и 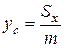 (14)
(14)
5. Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. Мl = m•d2. Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
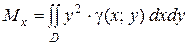 и
и 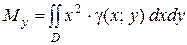 (15)
(15)
Момент инерции фигуры относительно начала координат – по формуле Мо=Мх +Му.
6. Площадь поверхности
Пусть поверхность S задана явным уравнением z=ƒ(х;у). D – её проекция на плоскость хОу. И в этой области функция z=ƒ(х;у) однозначна, непрерывна и имеет непрерывные частные производные первого порядка по х и по у. Тогда
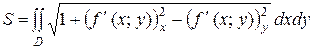 (16)
(16)
Пример.
Найти массу, статические моменты Sx и Sy и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 
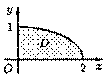 и координатными осями (см. рис). Поверхностная плотность в каждой точке фигуры =(х;у)= 30 • ху.
и координатными осями (см. рис). Поверхностная плотность в каждой точке фигуры =(х;у)= 30 • ху.
Решение: По формуле (12) находим массу пластинки.
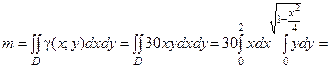
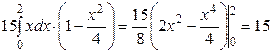
Находим статические моменты
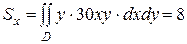 ,
, 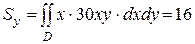
и координаты центра тяжести пластинки.
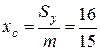 ,
, 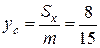 .
.
ТРОЙНОЙ ИНТЕГРАЛ
1. Основные понятия
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Определение.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция u =ƒ(х; у; z). Разбив область V сеткой поверхностей на n частей 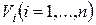 и выбрав в каждой из них произвольную точку Мi(хi; yi; zi), составим интегральную сумму для функции ƒ(х; у; z) по области V
и выбрав в каждой из них произвольную точку Мi(хi; yi; zi), составим интегральную сумму для функции ƒ(х; у; z) по области V
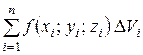 (здесь ∆Vi – объем элементарной области Vi). (1)
(здесь ∆Vi – объем элементарной области Vi). (1)
Если предел интегральной суммы существует и конечен при неограниченном увеличении числа n таким образом, что каждая «элементарная область» Vi стягивается в точку (т. е. диаметр области di стремится к нулю, т. е. di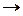 0), то его называют тройным интегралом от функции u =ƒ(х; у; z) по области V и обозначают
0), то его называют тройным интегралом от функции u =ƒ(х; у; z) по области V и обозначают
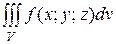 (или
(или 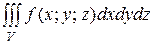 )
)
Таким образом, тройной интеграл определяется равенством
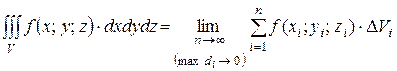 (2)
(2)
Здесь dv=dx dy dz - элемент объема.
Теорема (существования).
Если функция u=f(x; y; z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (1) при n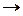 ∞ и max di
∞ и max di 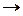 0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек Мi(хi; yi; zi) в них.
0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек Мi(хi; yi; zi) в них.
2. Основные свойства тройного интеграла
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
1). 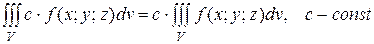 , линейность.
, линейность.
2). 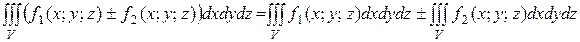
3). Если область V разбить на две области V1 и V2, такие, что V=V1UV2, а пересечение V1 и V2 состоит лишь из границы, их разделяющей, то
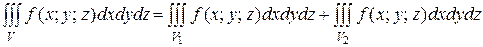 , аддитивность.
, аддитивность.
4). Если в области V функция f(x;y;z)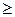 0, то и
0, то и 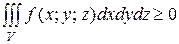 . Если в области интегрирования ƒ(х;у;z)
. Если в области интегрирования ƒ(х;у;z)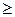
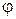 (x;y;z), то и
(x;y;z), то и
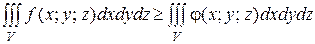
5). 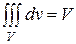 , так как в случае f(x;y;z)=1, любая интегральная сумма имеет вид
, так как в случае f(x;y;z)=1, любая интегральная сумма имеет вид 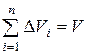 и численно равна объему тела.
и численно равна объему тела.
6). Оценка тройного интеграла:
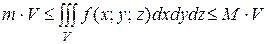 ,
,
где m и М - соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V. А f(x;y;z) непрерывна в замкнутой области V.
7). Теорема о среднем значении: если функция f(x;y;z) непрерывна в замкнутой области V, то в этой области существует такая точка Mo(xo;yo;zo), что
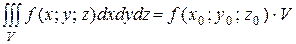 , где V - объем тела. f(x0;y0;z0) – среднее значение функции f(x;y;z) в области V.
, где V - объем тела. f(x0;y0;z0) – среднее значение функции f(x;y;z) в области V.
3. Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Пусть область интегрирования V является тело, ограниченное снизу поверхностью 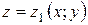 , сверху – поверхностью
, сверху – поверхностью 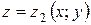 , причём
, причём 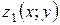 и
и 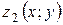 - непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху.
- непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху.
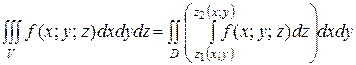
Если область D ограничена линиями х=а, х=в (а<в), у=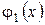 и у=
и у=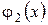 , где
, где 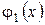 и
и 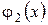 - непрерывные на отрезке
- непрерывные на отрезке 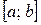 функции, причём
функции, причём 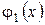
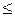
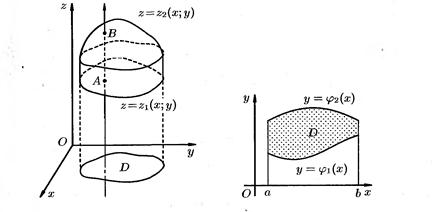
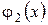 (см. рис.), то, переходя от двойного интеграла к повторным, получаем формулу по которой вычисляется тройной интеграл в декартовых координатах:
(см. рис.), то, переходя от двойного интеграла к повторным, получаем формулу по которой вычисляется тройной интеграл в декартовых координатах:
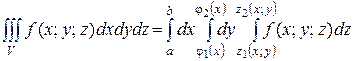 (3)
(3)
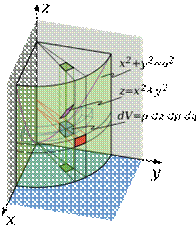 4. Выражение тройного интеграла через цилиндрические координаты
4. Выражение тройного интеграла через цилиндрические координаты
В некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
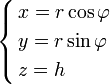 (4)
(4)
Модуль якобиана отображения равен  . Таким образом, получаем, что
. Таким образом, получаем, что
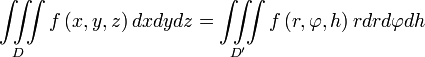 (5)
(5)
Здесь 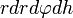 является элементом объема в цилиндрических координатах.
является элементом объема в цилиндрических координатах.
 5. Выражение тройного интеграла через сферические координаты
5. Выражение тройного интеграла через сферические координаты
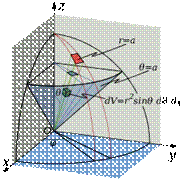
Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
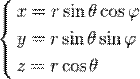 (6)
(6)
Модуль якобиана отображения равен 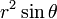 . Таким образом, получаем, что
. Таким образом, получаем, что
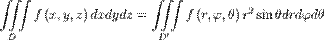 (7)
(7)
Здесь 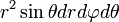 является элементом объема в сферических координатах.
является элементом объема в сферических координатах.
6. Приложения тройных интегралов
| Наименование величины | Общее выражение | Прямоугольные координаты | Цилиндрические координаты | Сферические координаты |
| Объем тела | 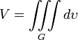
| 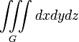
| 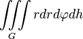
| 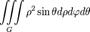
|
| Статические моменты относительно координатных плоскостей | 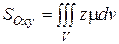 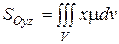 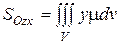
| |||
| Масса физического тела с плотностью μ | 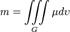
| 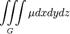
| 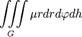
| 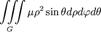
|
| Моменты инерции геометрического тела относительно координатных плоскостей | 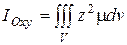 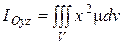 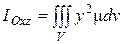
| ----------------- | --------------- | ----------------- |
| Моменты инерции геометрического тела относительно координатных осей | 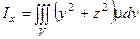 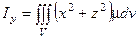 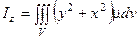
| ---------------- | -------------- | --------------- |
| Момент инерции геометрического тела относительно оси OZ | 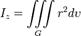
| 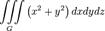
| 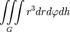
| 
|
| Координаты центра тяжести тела | 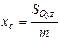
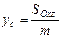
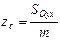
| ------------------ | ----------- | ------------- |
| Координаты центра тяжести однородного тела | 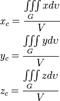
| 
| — | — |
Задачи.
1. Найти объём тела, ограниченного параболоидом 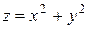 и плоскостью
и плоскостью 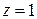 .
.
Отв. 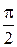 .
.
2. Вычислить 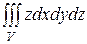 , где V – область, ограниченная верхней частью конуса
, где V – область, ограниченная верхней частью конуса 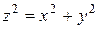 и плоскостью
и плоскостью 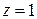 . Отв.
. Отв. 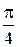 .
.
 3. Вычислить
3. Вычислить 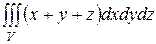 , где V – область, ограниченная поверхностями
, где V – область, ограниченная поверхностями 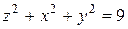 ,
, 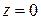 ,
, 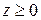 .
.
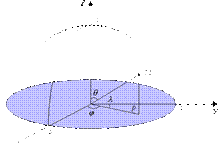
Решение. Перейдём в интеграле к сферическим координатам по формулам (6). Тогда область интегрирования можно задать неравенствами
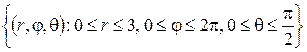 .
.
А, значит,
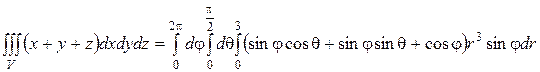 =…
=…
Отв. 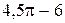 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление объемов | | | КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ |
Дата добавления: 2014-02-28; просмотров: 1374; Нарушение авторских прав

Мы поможем в написании ваших работ!