Принципы определения местоположения пунктов

Исходные данные при определении пространственных прямоугольных координат пункта по результатам спутниковых наблюдений:

массив {X, Y, Z}_{j= 1, 2, 3, 4} пространственных прямоугольных координат четырех навигационных ИСЗ;

результаты {R} _{j= 1, 2, 3, 4} синхронных одномоментных измерений дальностей между фазовым центром антенны приемника, установленного на пункте, и соответствующим НИСЗ.

Допустим, что на некоторый момент времени заданы пространственные прямоугольные координаты Х_i, Y_i, Z_i искусственного спутника Земли, обозначенного на рисунке 5.7 как «НИСЗ 1». С целью определения пространственных прямоугольных координат Х_P, Y_P, Z_P пункта Р (см. рис. 7.6) измеряют расстояние R_i между определяемым пунктом и искусственным спутником Земли.

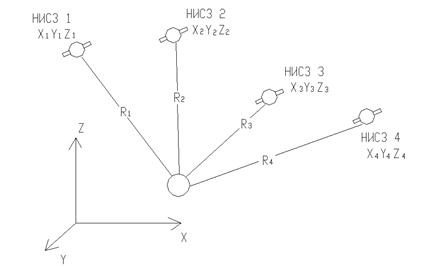
Рис. 7.6. Пространственная линейная засечка

Из рисунка 5.6 следует, что

R²₁ = DX²_1-P + DY²_1-P + DZ²_1-P,

где DX_{1 – P} = X_P – X_НИСЗ1 ; DY_{1 – P} = Y_P – Y_НИСЗ1 ; DZ_{1 – P} = Z_P – Z_НИСЗ1 ;

В уравнении имеем три неизвестных параметра — пространственные прямоугольные координаты определяемого пункта: Хр, Ypи Zp. Допустим, что одновременно с расстоянием R₁измерены также расстояния R₂ и R3 (рис. 7.6) между определяемым пунктом и еще двумя НИСЗ с известными (заданными) координатами. По результатам этих измерений, по аналогии с приведенным уравнением, можно написать соответствующие выражения для расстояний R₂ и R₃. Будем иметь систему уравнений, в которой число уравнений и число неизвестных равны между собой (три уравнения с тремя неизвестными):

R²_1-P = DX²_1-P + DY²_1-P + DZ²_1-P;

R²_2-P = DX²_2-P + DY²_2-P + DZ²_2-P;

R²_3-P = DX²_3-P + DY²_3-P + DZ²_3-P;

В приведенной системе уравнений три неизвестных — пространственные прямоугольные координаты определяемого пункта. Следовательно, решая данную систему, можно вычислить координаты Х_P, Y_P, Z_P, т. е. определить абсолютное положение пункта. Рассмотренное геометрическое построение называют пространственной линейной засечкой.

На практике метод пространственной линейной засечки реализуют при спутниковых наблюдениях, измеряя не расстояния до искусственных спутников Земли, а, так называемые, «псевдодальности». Последние отличаются от принятого понятия «дальности» на некоторую неизвестную, но постоянную на данный момент спутниковых наблюдений величину DD, обусловленную расхождением шкал времени искусственного спутника Земли и приемника спутниковых сигналов. Следовательно, при измерении абсолютного положения число неизвестных будет не три, а четыре (Х_p, Y_p, Z_P и DD). Отсюда следует, что для установления абсолютного положения пунктов на земной поверхности необходимо провести соответствующие наблюдения до четырех НИСЗ.

Понятие «псевдодальность» имеет следующий смысл. При радиотехнических измерениях расстояние характеризуется временем распространения сигнала от излучателя (передатчика) до приемника излучения.

В случае, когда излучатель и приемник находятся в разных точках пространства, измерение расстояния возможно только при строгой идентичности и синхронности шкал времени передатчика и приемника. Тогда время распространения сигнала от передатчика до приемника определяется как временной интервал между моментом излучения сигнала (временной метки), передаваемым передатчиком в составе соответствующей цифровой информации, и моментом его приема, отсчитываемым по шкале времени приемника.

В глобальных навигационных спутниковых системах указанные условия выполняются только в части, относящейся к навигационным спутникам, бортовые шкалы времени (БШВ) которых формируются бортовыми эталонами частоты (атомными эталонами частоты), синхронизированными с системной шкалой времени (СШВ), вырабатываемой в системах контроля и управления ГНСС и связанными с национальными стандартами частоты.

Для синхронизации БШВ и СШВ в системах контроля и управления ГНСС предусмотрена соответствующая сверка БШВ и СШВ. При необходимости проводят соответствующую синхронизацию БШВ и СШВ с точностью до десятков наносекунд.

Шкала времени в приемниках спутниковых сигналов (шкала времени потребителя — ШВП) задается в момент включения приемника («время старта»), вырабатывается с помощью соответствующего кварцевого опорного генератора и формируется автономно. Следовательно, шкала времени потребителя имеет случайное начальное расхождение с системной шкалой времени. Имеет также место последующий уход ШВП в процессе измерений относительно бортовой шкалы времени спутника, а, следовательно, и системной шкалы времени. При этом разность между приемом метки времени, отсчитанной по шкале времени потребителя, и моментом ее излучения по системной шкале времени дает совокупное значение времени распространения сигнала и расхождения шкалы времени потребителя (приемника) со шкалой системного времени на момент измерения (рис. 7.7).

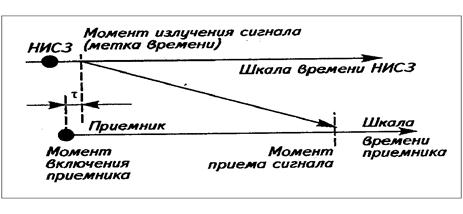
Рис. 7.7. К понятию «псевдодальность»

Псевдодальностью р_Ji между J-м приемником (точнее, между фазовым центром его антенны) и i-м навигационным ИСЗ называют величину

r_Ji = Сt_Ji,

где С— скорость распространения сигнала по трассе «НИСЗ-приемник»; t_Ji — временной интервал между моментом излучения сигнала, определяемый в системной шкале времени, и моментом его приема, отсчитанным в бортовой шкале времени приемника.

Псевдодальность r отличается от «истинной» дальности D на

DD_Ji = СDt_Ji,

где Dt_Ji - соответствующее расхождение шкал времени.

Если приемник работает на нескольких каналах, т.е. принимает сигналы нескольких передатчиков (разных НИСЗ) одновременно, то составляющая псевдодальности DD, определяемая расхождением временных шкал, будет одинаковой для всех каналов. Разность псевдодальностей, полученных в любой паре каналов приемника (от любой пары НИСЗ), — равна разности истинных дальностей от приемника до соответствующих НИСЗ на момент приема сигналов.

Точность определения положения с помощью пространственной линейной засечки (без учета влияния погрешностей положения НИСЗ) зависит как от точности измерения соответствующих расстояний (псевдодальностей), так и от геометрии засечки. Эта точность, как говорят, зависит от «геометрического фактора» ГФ — отношения стандартов погрешностей определения месторасположения M_t и измерения расстояний (псевдодальностей), m_R между НИСЗ и определяемой точкой на земной поверхности, т. е.

ГФ = M_t / m_R .

Различают:

геометрический фактор, характеризующий суммарное влияние геометрии построения на точность определения планового положения пункта — ГФ_Н;

геометрический фактор, характеризующий суммарное влияние геометрии построения на точность определения абсциссы пункта — ГФ_Х;

геометрический фактор, характеризующий суммарное влияние геометрии построения на точность определения ординаты пункта — ГФ_У;

геометрический фактор, характеризующий суммарное влияние геометрии построения на точность положения пункта по высоте — ГФ_V.

Применительно к системе GPS понятию ГФ соответствует понятие «ухудшение точности» — DOP. При этом, геометрическому фактору ГФ_Н соответствует HDOP, а геометрическому фактору ГФv-VDOP.

Геометрический фактор, определяющий точность пространственного положения пункта, называют PDOP («пидоп»).

Дата добавления: 2014-02-28; просмотров: 1053; Нарушение авторских прав

Мы поможем в написании ваших работ!