
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сходимость ряда
Числовые ряды.
Лекция 12
План лекции
1. Сходимость числового ряда.
2. Признаки сходимости рядов
3. Знакопеременные ряды.
Если  числовая последовательность, то числовым рядомназывается бесконечная сумма
числовая последовательность, то числовым рядомназывается бесконечная сумма
u1+ u2 + …..+ un= 
 (1)
(1)
Числа u1, u2, ....,un,… называются членами ряда, а un – общим членом ряда.
Обозначим суммы конечного числа членов ряда:
s1 = u1; s2 = u1 + u2; ….; sn = u1+ u2 + ….+ un,
Sn называется n-й частичной суммой ряда.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.


Число S называется суммой ряда. Если конечного предела последовательности Sn не существует, ряд называется расходящимся .
Пример. Найти сумму ряда 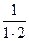 +
+ 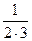 +
+ 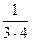 + ….+
+ ….+ 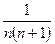 +
+
Решение. n-я частичная сумма ряда:
Sn = 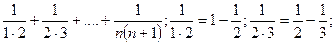


| <== предыдущая страница | | | следующая страница ==> |
| Линейные ДУ 2-го порядка с постоянными коэффициентами | | | Свойства сходящихся рядов |
Дата добавления: 2014-02-28; просмотров: 491; Нарушение авторских прав

Мы поможем в написании ваших работ!