Пример 4. Горизонтальной платформе радиуса r весом Р, имеющей вертикальную ось, проходящую через центр платформы О

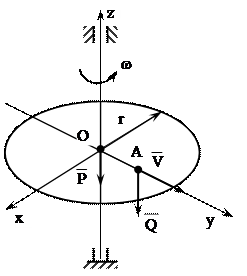Горизонтальной платформе радиуса r весом Р, имеющей вертикальную ось, проходящую через центр платформы О, сообщается начальная угловая скорость w₀. Человек А весом Q, находившийся в начальный момент в центре платформы, идет вдоль радиуса ОВ. Найти угловую скорость вращения платформы w при ОА=r, принимая платформу за однородный диск.

Решение. Используем для решения теорему об изменении кинетического момента относительно неподвижного центра

спроектируем это равенство на ось вращения Z

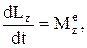
но 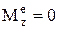, тогда L_z=const.

В начальный момент

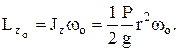
В конце движения

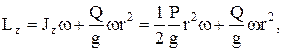
приравнивая правые части

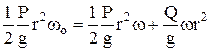
и сократив на 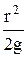, получим

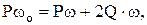
откуда

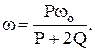
Итак, доказаны три теоремы динамики системы, которые ставят в соответствие векторные меры движения и 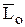векторным же мерам действия сил 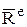и 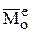. Во всех трёх теоремах исключены внутренние силы.

Контрольные вопросы

1. Как определяется момент силы относительно центра и оси?

2. Как определяется момент количества движения материальной точки относительно центра и оси?

3. Что такое кинетический момент механической системы?

4. Как формулируются частные случаи теоремы моментов?

Переходим к рассмотрению четвертой теоремы. Эта теорема по сравнению с тремя предыдущими имеет ряд особенностей: во-первых, она связывает между собой скалярные меры движения со скалярными мерами действия сил, во-вторых, в ней не исключены внутренние силы, и в-третьих, доказанная для одной точки, она распространяется на всю механическую систему.

14. Кинетическая энергия

Кинетической энергией материальной точки будем называть половину произведения массы точки на квадрат её скорости:

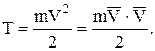
Эта величина всегда положительна, и поэтому кинетическую энергию механической системы будем определять как арифметическую сумму кинетических энергий отдельных точек:

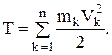
Скалярной мере движения необходимо поставить в соответствие скалярную меру действия сил.

15. Работа и мощность силы

Работу постоянной силы на конечном прямолинейном перемещении из точки М₁ в точку М₂ можно представить следующим образом:

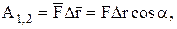
или

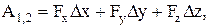
где F_x, F_y, F_z – проекции вектора 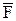на оси x, y, z;

∆x, ∆y, ∆z – проекции вектора 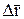на те же оси.

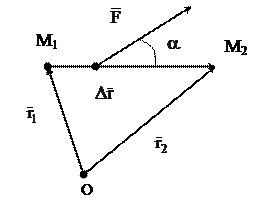Если же требуется определить работу на криволинейном перемещении точки приложения переменной силы, то следует всё это конечное перемещение разбить на бесконечно большое количество бесконечно малых участков, определить работу на каждом участке, а затем эти работы просуммировать.

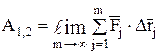(24)

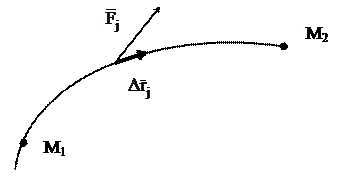
Произведение под знаком суммы при бесконечном уменьшении 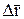называется элементарной работой:

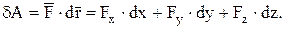
В общем случае выражение в правой части равенства не является полным дифференциалом некоторой функции координат, т. к. сила может быть функцией скорости или времени.

Ещё одной скалярной мерой действия сил является мощность – это отношение элементарной работы к дифференциалу времени: 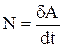, имея в виду, что 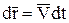, а 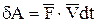, запишем:

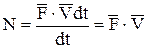, (25)

или

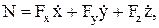
где 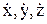– проекции скорости на оси координат x, y, z.

16. Теорема об изменении кинетической энергии

Запишем основное уравнение динамики точки:

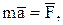
или

.

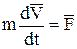Умножим скалярно правую и левую части равенства на :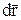

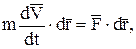
замечая, что 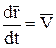, запишем:

.

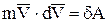Имея в виду, что

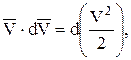
получим:

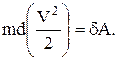
Так как масса точки во время движения не меняется, то

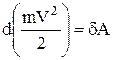
и окончательно получим:

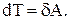(26)

Дифференциал кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.

Разделив правую и левую части на dt, получим:

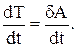
В правой части записано выражение, определяющее мощность всех сил, приложенных к материальной точке:

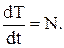(27)

Таким образом, формулировка второй дифференциальной формы теоремы энергии может быть записана следующим образом: «Производная по времени от кинетической энергии материальной точки равна мощности сил, приложенных к точке».

Третья, интегральная, форма теоремы может быть получена интегрированием правой и левой части равенства (18) в пределах от М₁ до М₂ по траектории перемещения материальной точки:

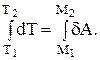(28)

Правая часть равенства представляет собой работу сил, приложенных к точке, тогда

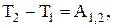(29)

т. е. изменение кинетической энергии материальной точки на некотором перемещении равно работе сил, приложенных к этой точке на том же перемещении.

Следует заметить также, что интеграл в правой части равенства (28) в общем случае имеет вид

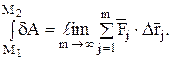
Полученную теорему, не изменяя обозначений, можно распространить и на механическую систему, имея в виду, что кинетическая энергия определяется для всей системы, а работа подсчитывается для внешних и внутренних сил.

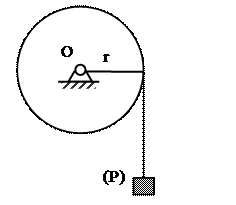Пример 5

На шкив радиуса r весом Q, вращающийся вокруг горизонтальной оси О, навернута веревка, к концу которой привязана гиря весом Р; в начале система находится в покое. Найти угловую скорость шкива в тот момент, когда груз опустится на расстояние h.

Решение: Применим теорему об изменении кинетической энергии Т₂-Т₁=А_1,2. Но Т₁=0, тогда Т₂=А_1,2

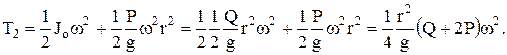
Работу совершает только сила тяжести груза

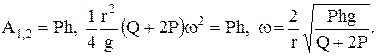
Контрольные вопросы

1. Что называется кинетической энергией материальной точки?

2. Как определяется работа и мощность силы?

3. Как определяется элементарная работа силы?

4. Как формулируются дифференциальные и интегральная формы теоремы об изменении кинетической энергии?

Библиографический список

1. Айзерман М.А. Классическая механика. М.: Наука, 1974. 368 с.

2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. М.: Наука, 1970. Т.2. 460 с.

3. Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 1995. 415 с.

4. Яблонский А.А. Курс теоретической механики. М.: Высшая школа, 1971. Ч. 1. 275 с.

5. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. М.: Высшая школа, 1983. 532 с.

6. Сборник заданий для курсовых работ по теоретической механике. Учеб. пособие для вузов./ Под ред. А.А Яблонского. и др. М.: Высшая школа, 1985. 367 с.

7. Бать М.И. и др. Теоретическая механика в примерах и задачах /М.И.Бать, Г.Ю.Джанелидзе, А.С.Кельзон. М.: Физматгиз, 1961. Ч.1. 457 с.

8. Мещерский Н.В. Сборник задач по теоретической механике. М.: Наука, 1971. 450 с.

Дата добавления: 2014-02-26; просмотров: 489; Нарушение авторских прав

Мы поможем в написании ваших работ!