Пример 3

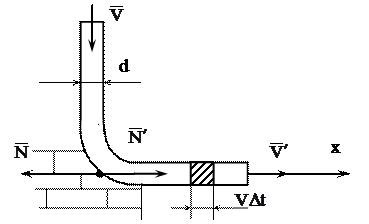Определить горизонтальную составляющую N возникающего при движении воды давления на опору колена трубы диаметром d, по которой течет вода со скоростью V. Плотность воды – r.

Решение. Применим для решения этой задачи теорему об изменении количества движения в интегральной форме

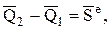
а в проекции на ось Х

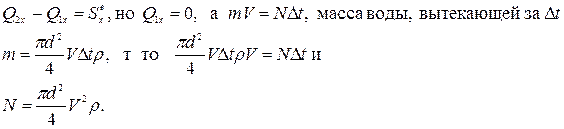
Контрольные вопросы

1. Как определяется количество движения механической системы?

2. Что такое импульс силы?

3. Как формулируется теорема об изменении количества движения?

4. Как формулируется закон сохранения количества движения?

5. Чему равно количество движения тела, вращающегося вокруг неподвижного центра масс?

10. Момент количества движения материальной точки.

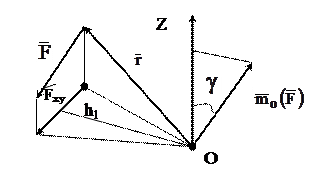Эта мера движения вводится по аналогии с моментом силы относительно центра и оси. Моментом силы относительно центра О является векторное произведение:

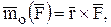
а моментом силы относительно оси Z является проекция вектора – момента ­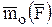 на ось Z:

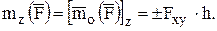
Момент количества движения точки относительно центра О соответственно:

,

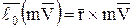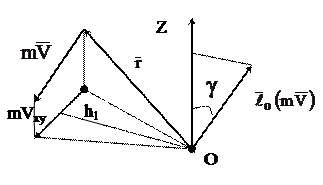
а момент количества движения относительно оси Z

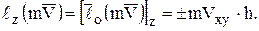
При этом знак “+” будет в том случае, когда со стороны оси виден поворот векторов 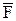и 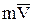против часовой стрелки.

11. Кинетический момент

Главный момент количества движения механической системы, который обычно называют кинетическим моментом относительно центра, определится как геометрическая сумма моментов количеств движения материальных точек относительно центра:

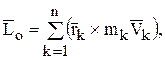
а алгебраическую сумму моментов количеств движения относительно оси называют кинетическим моментом относительно оси:

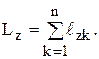
12. Обобщенная теорема моментов

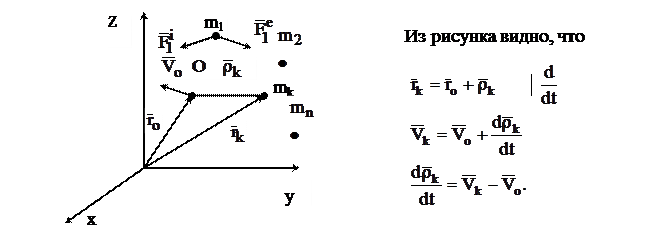
Если точка о (центр моментов) движется произвольно, то кинетический момент относительно центра О равен:

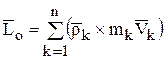. (19)

Возьмём производную по времени от этого выражения:

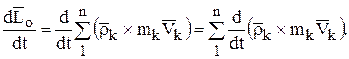
Имея в виду, что 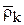и 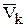величины переменные, имеем:

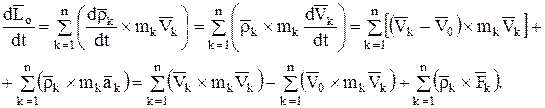
как векторное произведение коллинеарных векторов.

Преобразуем суммы:

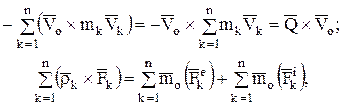
но ,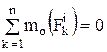

тогда: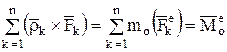

и окончательно получим:

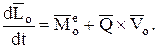(20)

Это и есть математическая запись обобщенной теоремы моментов.

Производная по времени от кинетического момента относительно центра О равна сумме главного момента внешних сил относительно того же центра и векторного произведения количества движения механической системы на скорость центра моментов.

13. Частные случаи теоремы моментов

1. Если центр моментов неподвижен, то 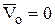и ,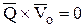

тогда

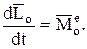(21)

Это выражение следует назвать теоремой моментов относительно неподвижного центра.

2. Если центр моментов совпадает с центром масс механической системы, то

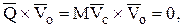
при этом

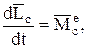(22)

а это выражение есть теорема моментов относительно центра масс.

3. Если центр моментов имеет скорость, коллинеарную скорости центра масс:

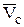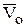║ , то

тогда

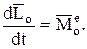(23)

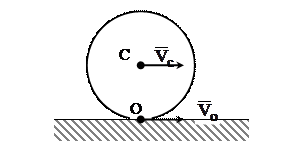Этот частный случай весьма продуктивен при решении задач, где в качестве центра моментов целесообразно использовать точку, движущуюся параллельно центру масс, например, точку касания катящегося колеса.

В этом случае удаётся исключить неизвестные реакции, возникающие в этой точке.

Дата добавления: 2014-02-26; просмотров: 484; Нарушение авторских прав

Мы поможем в написании ваших работ!