
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
УРАВНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА ЧЕРЕЗ А-ПАРАМЕТРЫ
Токи всех ветвей линейной цепи при воздействии нескольких ЭДС определяются как сумма частичных токов, получаемых последовательным подключением каждой из этих ЭДС при условии, что все остальные ЭДС равны нулю.
Рис.10.6 - Условные положительные направления токов и напряжений при определении Y-параметров
УРАВНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА ЧЕРЕЗ Y-ПАРАМЕТРЫ
Пусть заданными являются напряжения U1 и U2, а искомыми величинами – токи I1 и I2. Как видно из таблицы 10.2, в этом случае четырехполюсник будет описываться системой Y-параметров. Выясним физический смысл этих параметров. При этом условные положительные направления токов I1 и I2 согласно таблицы 10.2 выбираются встречными(рис. 10.6).
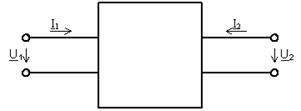
Комплексные напряжения U1 и U2 можно рассматривать как два независимых воздействия, каждое из которых влияет на токи I1 и I2.
Для линейного четырехполюсника справедлив принцип суперпозиции (наложения):
Тогда согласно принципа наложения входной и выходной токи четырехполюсника равны сумме частичных токов:
I1 = I11|U2=0 + I12|U1=0 , (10.7)
I2 = I21|U2=0 + I22|U1=0 , (10.8)
где I11 – частичный ток во входной ветви, вызываемый напряжением U1
при U2 = 0 (рис.10.7, а);
I12 – частичный ток во входной ветви, вызываемый напряжением U2
при U1 = 0; (рис.10.7, б);
I21 – частичный ток в выходной ветви, вызываемый напряжением U1
при U2 = 0 (рис.10.7, а);
I22 – частичный ток в выходной ветви, вызываемый напряжением U2
при U1 = 0; (рис.10.7, б);
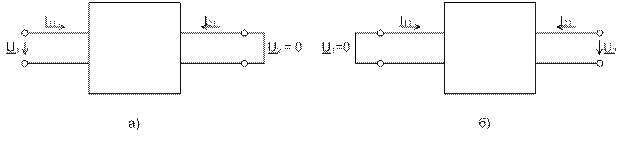
Рис.10.7. К определению частичных токов
Частичные токи и напряжения U1 и U2 связаны между собой соотношениями
I11 = Y11U1; I12 = Y12U2; I21 = Y12U1; I22 = Y22U2.
Подставив выражения для частичных токов в (10.7) и (10.8), получим систему уравнений четырехполюсника через Y-параметры:
| |
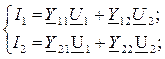 (10.9)
(10.9)
или в матричной форме:
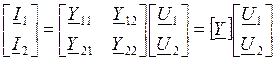
Коэффициенты Y11, Y12, Y21, Y22 называются Y-параметрами четырехполюсника. Они являются комплексными величинами и зависят от частоты. Y-параметры имеют размерность проводимостей, могут быть определены при помощи опытов короткого замыкания и имеют следующий физический смысл:
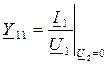 (10.10) – комплексная входная проводимость со стороны зажимов 1-1' в режиме короткого замыкания на зажимах 2-2';
(10.10) – комплексная входная проводимость со стороны зажимов 1-1' в режиме короткого замыкания на зажимах 2-2';
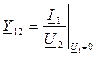 (10.11) – комплексная передаточная проводимость обратной передачи от зажимов 2-2' к зажимам 1-1' в режиме короткого замыкания на зажимах 1-1';
(10.11) – комплексная передаточная проводимость обратной передачи от зажимов 2-2' к зажимам 1-1' в режиме короткого замыкания на зажимах 1-1';
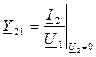 (10.12) – комплексная передаточная проводимость прямой передачи от зажимов 1-1' к зажимам 2-2' в режиме короткого замыкания на зажимах 2-2';
(10.12) – комплексная передаточная проводимость прямой передачи от зажимов 1-1' к зажимам 2-2' в режиме короткого замыкания на зажимах 2-2';
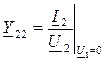 (10.13) – комплексная входная проводимость со стороны зажимов 2-2' в режиме короткого замыкания на зажимах 1-1'.
(10.13) – комплексная входная проводимость со стороны зажимов 2-2' в режиме короткого замыкания на зажимах 1-1'.
Из уравнений (10.9) – (10.13) вытекают следующие свойства Y-параметров:
1) у обратимых четырехполюсников Y12 = Y21, т.е. только три коэффициента в основных уравнениях линейных пассивных четырехполюсников являются независимыми;
2) у симметричных четырехполюсников Y12 = Y21 и Y11 = Y22 ; в этом случае число независимых коэффициентов равно двум.
Уравнения через А-параметры устанавливают связи между входными напряжением и током (U1, I1) и выходными напряжением и током (U2, I2).
Положительное направление токов I1 и I2 выбирается согласно рис. 10.5. Удобство выбора именно такого положительного направления тока I2 связано в данном случае с тем, что форма А применяется обычно при передаче электрической энергии от входных зажимов к выходным, причем четырехполюсник, включенный между источником и приемником, может состоять из нескольких четырехполюсников, соединенных каскадно: вход каждого последующего четырехполюсника совпадает с выходом предыдущего четырехполюсника.
Выведем уравнения четырехполюсника А-формы из уравнений Y-формы. При этом учтем, что положительное направление тока I2, противоположно положительному направлению в Y-форме. Для этого в уравнениях (10.1) ток I2 запишем с минусом:
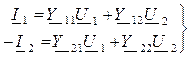 (10.14)
(10.14)
Из второго уравнения (10.14) следует:
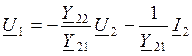 (10.15)
(10.15)
Подстановка этого выражения в первое уравнение (10.14) дает:
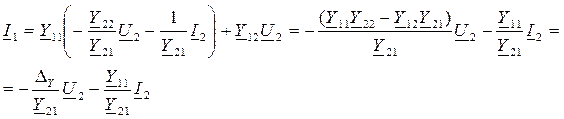 (10.16)
(10.16)
Положив в (10.15) и (10.16):
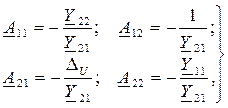 (10.17)
(10.17)
получим систему уравнений четырехполюсника через А-параметры:
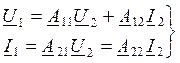 (10.18)
(10.18)
или в матричной форме
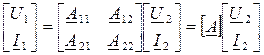 .
.
Коэффициенты А11, А12, А21, А22 в общем случае комплексные и зависят от частоты; А11 и А22 – безразмерные, А12 имеет размерность сопротивления, А21 имеет размерность проводимости. Эти коэффициенты могут быть определены аналогично предыдущему и имеют следующий физический смысл.
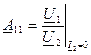 (10.19) – величина, обратная комплексному коэффициенту передачи по напряжению от зажимов 1-1' к зажимам 2-2' при холостом ходе на зажимах 2-2'.
(10.19) – величина, обратная комплексному коэффициенту передачи по напряжению от зажимов 1-1' к зажимам 2-2' при холостом ходе на зажимах 2-2'.
Следовательно, коэффициент А11 связан с коэффициентом передачи по напряжению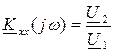 следующим образом:
следующим образом:
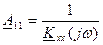 . (10.20)
. (10.20)
Последние соотношения удобно использовать при экспериментальном определении параметра А11.
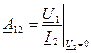 (10.21) – величина, обратная комплексной передаточной проводимости в режиме короткого замыкания на зажимах 2-2'.
(10.21) – величина, обратная комплексной передаточной проводимости в режиме короткого замыкания на зажимах 2-2'.
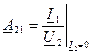 (10.22) – величина, обратная комплексному передаточному сопротивлению при холостом ходе на зажимах 2-2'.
(10.22) – величина, обратная комплексному передаточному сопротивлению при холостом ходе на зажимах 2-2'.
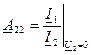 (10.23) – величина, обратная комплексному коэффициенту передачи по току от зажимов 1-1' к зажимам 2-2' в режиме короткого замыкания на зажимах 2-2'.
(10.23) – величина, обратная комплексному коэффициенту передачи по току от зажимов 1-1' к зажимам 2-2' в режиме короткого замыкания на зажимах 2-2'.
Следовательно, коэффициент А22 связан с коэффициентом передачи по току КIK3(jω) = I2/I1 следующим образом:
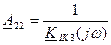 . (10.24)
. (10.24)
Из уравнений (10.17) – (10.24) вытекают следующие свойства А-параметров:
1) для обратимых четырехполюсников определитель, составленный из А-параметров равен единице:
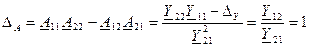 , (10.25)
, (10.25)
(т.к. Y12 = Y21), т.е. только три любых коэффициента в уравнениях (10.18) являются независимыми; четвертый коэффициент связан с остальными условием (10.25);
2) если четырехполюсник симметричен, то на основании (10.17) с учетом того, что Y11 = Y22, А11 = А22, т.е. число независимых коэффициентов равно двум.
| <== предыдущая страница | | | следующая страница ==> |
| ЧЕТЫРЕХПОЛЮСНИКА | | | Четырехполюсника. Характеристические параметры |
Дата добавления: 2014-03-03; просмотров: 845; Нарушение авторских прав

Мы поможем в написании ваших работ!