
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Математические сведения
Лекция 3. Закон сохранения момента импульса.
Момент силы. Момент импульса материальной точки и механической системы. Уравнение моментов механической системы. Закон сохранения момента импульса механической системы.
Векторным произведением двух (ненулевых) векторов 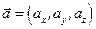 и
и 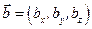 называется вектор
называется вектор 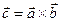 , который в декартовой системе координат (с ортами
, который в декартовой системе координат (с ортами 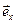 ,
, 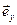 ,
, 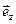 ) определяется по формуле:
) определяется по формуле:
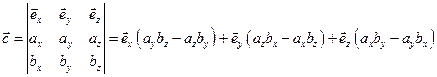 .
.
Модуль вектора 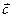 :
: 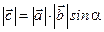 (площадь прямоугольника на векторах
(площадь прямоугольника на векторах 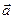 и
и 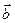 ).
).
Свойства векторного произведения.
1) Вектор 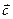 направлен перпендикулярно к плоскости векторов
направлен перпендикулярно к плоскости векторов 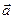 и
и 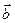 . Поэтому для любого вектора
. Поэтому для любого вектора 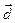 , лежащего в плоскости (линейно независимых) векторов
, лежащего в плоскости (линейно независимых) векторов 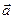 и
и 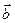 (т.е.
(т.е.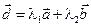 ), получаем
), получаем 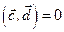 . Следовательно, если два ненулевых вектора
. Следовательно, если два ненулевых вектора 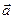 и
и 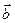 параллельны, то
параллельны, то 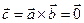 .
.
2) Производная по времени от векторного произведения – это вектор 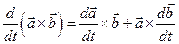 .
.
Действительно, (базисные векторы 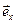 ,
, 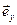 ,
, 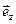 - постоянные):
- постоянные): 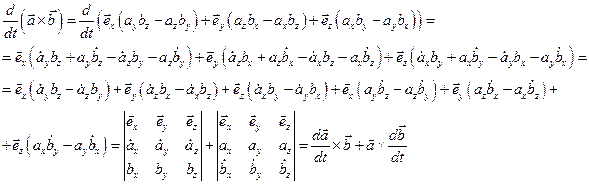
| <== предыдущая страница | | | следующая страница ==> |
| ЛОКАЛИЗАЦИЯ И ФУНКЦИИ ПИЩЕВОГО ЦЕНТРА | | | Вектор момента импульса |
Дата добавления: 2014-03-04; просмотров: 413; Нарушение авторских прав

Мы поможем в написании ваших работ!